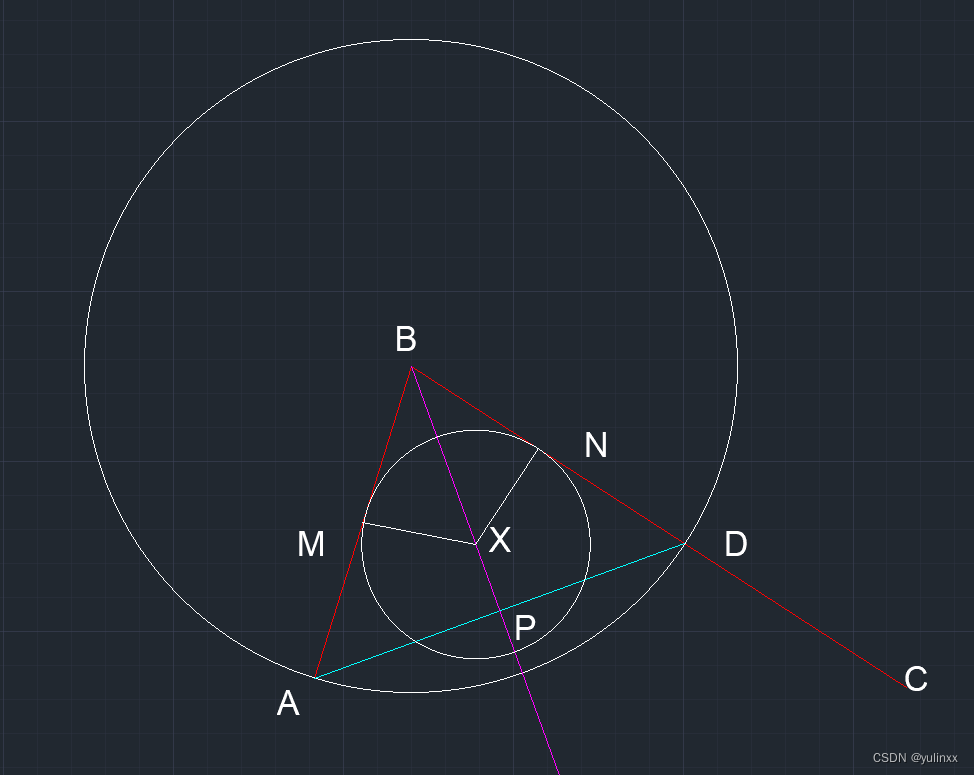
推导原理基本很简单：

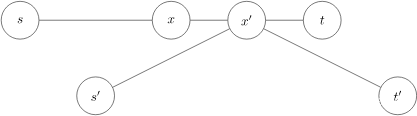
已知AB， BC两条线段，且交于B点，求倒角半径为 L，AB，BC的倒角

以最短边（假定为AB）长 LAB，
在BC中，以B为起点，找出与LAB同长度的点D，
即BD的长度等于AB的长度

(或 以B为圆心，LAB为半径， 绘制一个圆，
圆与AB交于A点， 于BC交于D点)

连接AD， 找出AD的中点P，

连接BP，
则BP为ABC夹角的角平分线

此时构成的 ABD,为一个等腰三角形
可轻松得出 垂直于BP的线， 到AB与BD的距离相等，即AP = PD
可样可用直角三角形法则得出 BP上的任意点，到AB的垂线，与到BC的垂线相等
即 XM = XN = L 圆弧半径

以X点作圆心，XM作半径，绘制圆，
该圆与AB， BC分别相切，

则圆弧 MN 则为AB与BC的倒角，倒角半径为L = XM

加上角度，长度，坐标的标记，如下：

---

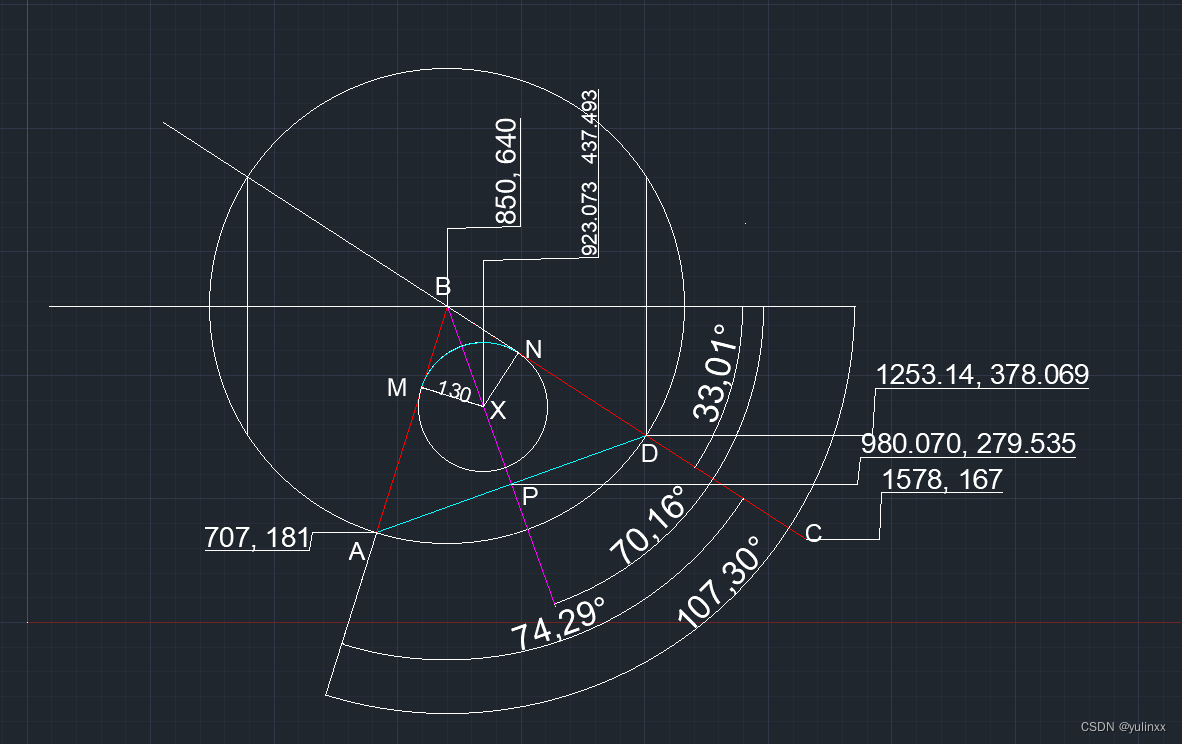
python算法：

import numpy as np
import math# 求单位向量
def unit_vector(vector):""" Returns the unit vector of the vector.  """return vector / np.linalg.norm(vector)# 角度
def angle_between(v1, v2):""" Returns the angle in radians between vectors 'v1' and 'v2'::>>> angle_between((1, 0, 0), (0, 1, 0))1.5707963267948966>>> angle_between((1, 0, 0), (1, 0, 0))0.0>>> angle_between((1, 0, 0), (-1, 0, 0))3.141592653589793"""v1_u = unit_vector(v1)v2_u = unit_vector(v2)return np.arccos(np.clip(np.dot(v1_u, v2_u), -1.0, 1.0))# 点乘
def dotproduct(v1, v2):return sum((a * b) for a, b in zip(v1, v2))# 向量的长度
def length(v):return math.sqrt(dotproduct(v, v))# 向量角度
def angle(v1, v2):return math.acos(dotproduct(v1, v2) / (length(v1) * length(v2)))def funcChamfer(ptA, ptB, ptC, lR):# ABC点 组成的部分向量vBA = [ptA[0] - ptB[0], ptA[1] - ptB[1]]vBC = [ptC[0] - ptB[0], ptC[1] - ptB[1]]# 求ABC的夹角aABC = angle_between(vBA, vBC)print(f'ABC的夹角 Radius {aABC}, Angle:{180.0 / math.pi * aABC}')# 向量 BA BC的长度lBA = length(vBA)lBC = length(vBC)print(f'向量 BA BC的长度  lBA:{lBA}, lBC:{lBC}')# 获得 BA BC 最短边边长 lShort# 以及需要长边的端点 ptLast， 用于计算D点lShort = 0  # 存储 AB BC中， 短边的边长ptShortS = None # 存储短边的起始点vShort = None    # 存储短边的向量vLong = None    # 存储长边的向量if(lBA <= lBC):lShort = lBAptShortS = ptAvShort = vBAvLong = vBCelse:lShort = lBCptShortS = ptCvShort = vBCvLong = lBA# --------------------求D点方式1(三角函数,复杂，仅做示范)：# 和X轴的夹角aShort = angle_between([1, 0], vShort)aLong = angle_between([1, 0], vLong)print(f'短边和X轴的夹角: Radius: {aShort}, Angle:{180.0 / math.pi * aShort}')print(f'长边和X轴的夹角: Radius: {aLong}, Angle:{180.0 / math.pi * aLong}')test = dotproduct(vBC, [1, 0])print(f'Test {test}')ptD = []ptD.append(ptB[0] + lShort * math.cos(math.pi * 2 - aLong))ptD.append(ptB[1] + lShort * math.sin(math.pi * 2 - aLong))print(f'point D:({ptD[0]}, {ptD[1]})')# --------------------求D点方式2(向量法）：# BC (长边）转单位向量：vNBC = unit_vector(vLong)x = [ptB[0], ptB[1]] + (vNBC * lShort)print(f'{vNBC}, ptD: {x}')# --------------------# AD点的中点PptPX = (ptD[0] + ptShortS[0]) * 0.5ptPY = (ptD[1] + ptShortS[1]) * 0.5 print(f'point P:({ptPX}, {ptPY})')# BP向量vBP = [ptPX - ptB[0], ptPY - ptB[1]]# 假定点为 X， X到AB的垂线为 XM，且XM = lR# 角ABP度数为 ABC的一半， 已知角度与XM的长度，# 则可求出 BX 长度 lBXlBX = lR / math.sin(aABC * 0.5)ptX = ptB + unit_vector(vBP) * lBXprint(f'ptX: {ptX}')return ptXif __name__ == '__main__':# AB，BC两线段交于B点  A,B,C如下ptA = [707, 181]ptB = [850, 640]    # 公共点ptC = [1578, 167]lR = 130.0   # 倒角圆半径ptX = funcChamfer(ptA, ptB, ptC, lR)print(f'以此点: {ptX} 为圆心,绘制圆弧') 

ABC的夹角 Radius 1.2966305334118693, Angle:74.29145715229679
向量 BA BC的长度  lBA:480.7598152924181, lBC:868.1664586932624
短边和X轴的夹角: Radius: 1.8728126012699295, Angle:107.30425787168404
长边和X轴的夹角: Radius: 0.5761820678580603, Angle:33.01280071938726
Test 728
point D:(1253.1405982438891, 378.0693640530776)
[ 0.83854887 -0.54482639], ptD: [1253.14059824  378.06936405]
point P:(980.0702991219446, 279.5346820265388)
ptX: [923.07255377 437.49319016]
以此点: [923.07255377 437.49319016] 为圆心,绘制圆弧

cpp算法：

待补充