文章目录
- 1. 使用两次DFS求得树的直径
- 2. 使用树形DP求得树的直径
- 3. 性质
- 4. 参考文献和习题
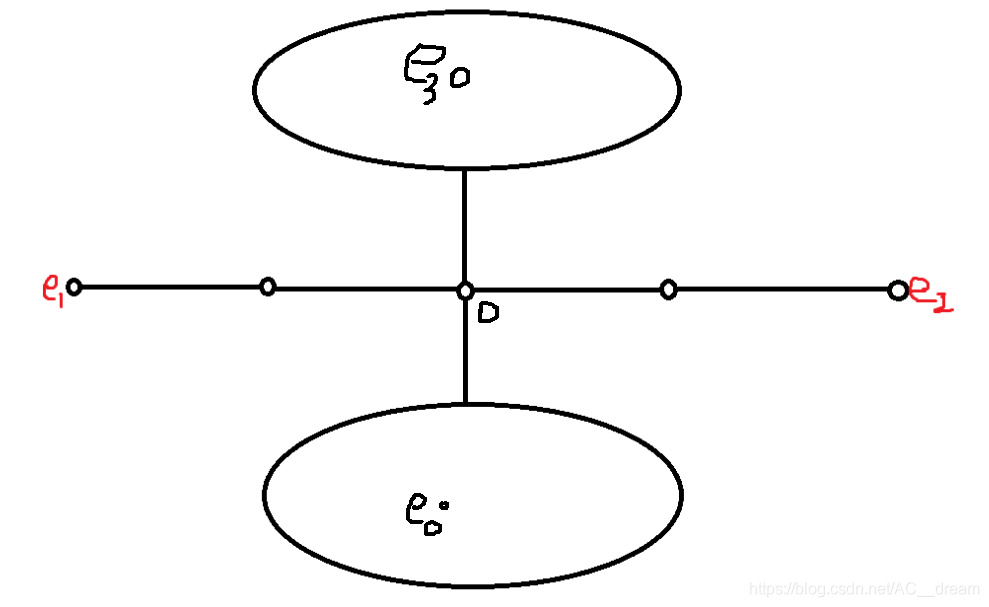
树上任意两节点之间最长的简单路径即为树的「直径」。显然,一棵树可以有多条直径,他们的长度相等。可以用两次 D F S / B F S DFS/BFS DFS/BFS 或者树形 D P DP DP 的方法在 O ( n ) O(n) O(n) 时间求出树的直径。
1. 使用两次DFS求得树的直径
两次 D F S / B F S DFS/BFS DFS/BFS 。第一次任意选一个点进行 D F S / B F S DFS/BFS DFS/BFS 找到离它最远的点,此点就是最长路的一个端点,再以此点进行 D F S / B F S DFS/BFS DFS/BFS ,找到离它最远的点,此点就是最长路的另一个端点,于是就找到了树的直径。
证明:
假设此树的最长路径是从 s s s到 t t t,我们选择的点为 u u u。反证法:假设搜到的点是 v v v。
-
- v v v在这条最长路径上,那么 d i s [ u , v ] > d i s [ u , v ] + d i s [ v , s ] dis[u,v]>dis[u,v]+dis[v,s] dis[u,v]>dis[u,v]+dis[v,s],显然矛盾。
-
- v v v不在这条最长路径上,我们在最长路径上选择一个点为 p o po po,则 d i s [ u , v ] > d i s [ u , p o ] + d i s [ p o , t ] dis[u,v]>dis[u,po]+dis[po,t] dis[u,v]>dis[u,po]+dis[po,t],那么有 d i s [ s , v ] = d i s [ s , p o ] + d i s [ p o , u ] + d i s [ u , v ] > d i s [ s , p o ] + d i s [ p o , t ] = d i s [ s , t ] dis[s,v]=dis[s,po]+dis[po,u]+dis[u,v]>dis[s,po]+dis[po,t]=dis[s,t] dis[s,v]=dis[s,po]+dis[po,u]+dis[u,v]>dis[s,po]+dis[po,t]=dis[s,t],即 d i s [ s , v ] > d i s [ s , t ] dis[s,v]>dis[s,t] dis[s,v]>dis[s,t],矛盾。
也许你想说 u u u本身就在最长路径,或则其它的一些情况,但其实都能用类似于上面的反证法来证明的。
综上所述,你两次 D F S / B F S DFS/BFS DFS/BFS 就可以求出最长路径的两个端点和路径长度。

上述证明过程建立在所有路径均不为负的前提下。如果树上存在负权边,则上述证明不成立。故若存在负权边,则无法使用两次 D F S / B F S DFS/BFS DFS/BFS 的方式求解直径。
代码实现如下:
const int N = 10000 + 10;int n, c, d[N];
//n是树节点数,c是第一次dfs找到的直径端点
//d[n]是所选根节点到某个下标点的最大距离
vector<int> E[N];
//E[n]是节点之间的连通情况,即edges//寻找以u为起始点/根节点,fa为前驱节点的,到u的最大距离的点
//即求直径端点c的过程
void dfs(int u, int fa) {for (int v : E[u]) {if (v == fa) continue; //不走回头路d[v] = d[u] + 1; //边权值均为1if (d[v] > d[c]) c = v; //如果更新后距离u的距离更大,更新cdfs(v, u);}
}int main() {//初始化图scanf("%d", &n);for (int i = 1; i < n; i++) {int u, v;scanf("%d %d", &u, &v);E[u].push_back(v), E[v].push_back(u);}dfs(1, 0); //第一次dfs找寻直径端点cd[c] = 0, dfs(c, 0); //第二次dfs找寻另一端点,前驱节点还是定为0printf("%d\n", d[c]); //输出旧c到新c的距离,即为树的直径return 0;
}如果需要求出一条直径上所有的节点,则可以在第二次 D F S DFS DFS 的过程中,记录每个点的前序节点,即可从直径的一端一路向前,遍历直径上所有的节点。
2. 使用树形DP求得树的直径
我们记录当 1 1 1 为树的根时,每个节点作为子树的根向下,所能延伸的最长路径长度 d 1 d_1 d1 与次长路径(与最长路径无公共边)长度 d 2 d_2 d2,那么直径就是对于每一个点,该点 d 1 + d 2 d_1 + d_2 d1+d2 能取到的值中的最大值。
树形 D P DP DP可以在存在负权边的情况下求解出树的直径。
const int N = 10000 + 10;int n, d = 0;
int d1[N], d2[N];
vector<int> E[N];void dfs(int u, int fa) {d1[u] = d2[u] = 0;for (int v : E[u]) {if (v == fa) continue;dfs(v, u);int t = d1[v] + 1;if (t > d1[u])d2[u] = d1[u], d1[u] = t;else if (t > d2[u])d2[u] = t;}d = max(d, d1[u] + d2[u]);
}int main() {scanf("%d", &n);for (int i = 1; i < n; i++) {int u, v;scanf("%d %d", &u, &v);E[u].push_back(v), E[v].push_back(u);}dfs(1, 0);printf("%d\n", d);return 0;}
如果需要求出一条直径上所有的节点,则可以在 D P DP DP 的过程中,记录下每个节点能向下延伸的最长路径与次长路径(定义同上)所对应的子节点,在求 d d d 的同时记下对应的节点 u u u,使得 d = d 1 [ u ] + d 2 [ u ] d = d_1[u] + d_2[u] d=d1[u]+d2[u],即可分别沿着从 u u u 开始的最长路径的次长路径对应的子节点一路向某个方向(对于无根树,虽然这里指定了 1 1 1 为树的根,但仍需记录每点跳转的方向;对于有根树,一路向上跳即可),遍历直径上所有的节点。
3. 性质
若树上所有边边权均为正,则树的所有直径中点重合
证明:使用反证法。设两条中点不重合的直径分别为 δ ( s , t ) \delta(s,t) δ(s,t) 与 δ ( s ′ , t ′ ) \delta(s',t') δ(s′,t′),中点分别为 x x x 与 x ′ x' x′。显然, δ ( s , x ) = δ ( x , t ) = δ ( s ′ , x ′ ) = δ ( x ′ , t ′ ) \delta(s,x) = \delta(x,t) = \delta(s',x') = \delta(x',t') δ(s,x)=δ(x,t)=δ(s′,x′)=δ(x′,t′)。
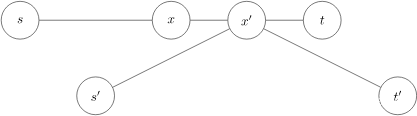
有 δ ( s , t ′ ) = δ ( s , x ) + δ ( x , x ′ ) + δ ( x ′ , t ′ ) > δ ( s , x ) + δ ( x , t ) = δ ( s , t ) \delta(s,t') = \delta(s,x) + \delta(x,x') + \delta(x',t') > \delta(s,x) + \delta(x,t) = \delta(s,t) δ(s,t′)=δ(s,x)+δ(x,x′)+δ(x′,t′)>δ(s,x)+δ(x,t)=δ(s,t),与 δ ( s , t ) \delta(s,t) δ(s,t) 为树上任意两节点之间最长的简单路径矛盾,故性质得证。
4. 参考文献和习题
OI_Wiki_树的直径
PT07Z - Longest path in a tree