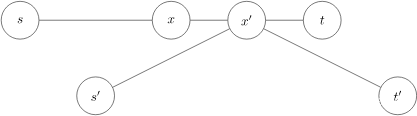
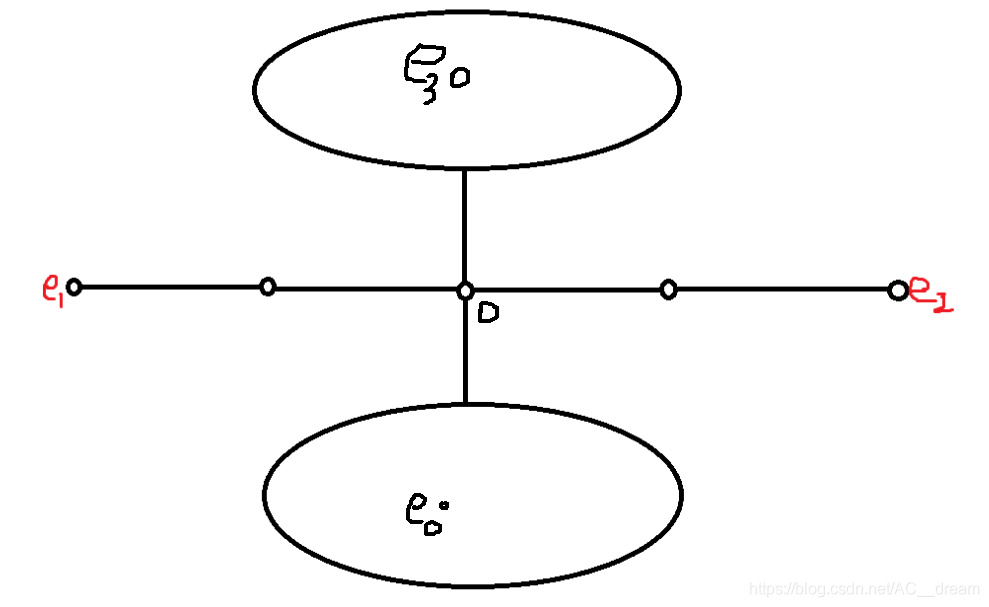
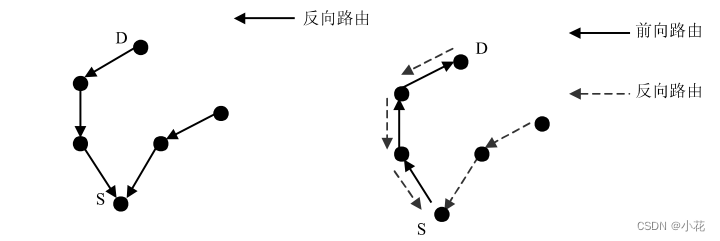
题解：分析一下，由于是树，所以两点之间的路径有且只有一条，为了求出欧拉路，所以必然会向回走，从递归的角度来看，假设x看作一个树根，有t个孩子y1…yt。其中每个孩子为根的子树欧拉路都加起来，然后去掉最长的两条欧拉路作为起点和终点。所以其实就是所有边权重之和的二倍减去树的直径（即树中最长的简单路）。
所以此题的关键是求出树的直径，算是经典问题之一，有两种方法。

树形dp：dp[x]表示经过x的最长简单路，用ans表示直径。转移方程为：dp[x] = max{dp[yi] + w}，其中yi为x的一个孩子，w为权重。ans = max（ans，dp1[x] + dp2[x]）也就是选出其中最长的两条简单路相加。

两次dfs（或者bfs）：从任意一点开始，dfs找到距离该点最远的节点，这个节点必然是树的直径端点之一（证明）然后第二次dfs从一个端点出发，求出直径长度。

import java.util.*;public class Main implements Runnable{private final int mod = 1000000007, max = 200005;private int [] dp1 = new int[max], dp2 = new int[max];//dp[x] 经过x的最长路径，和次长路径private List<Edge>[] g = new List[max];private int d = 0, deepest = 0;public static void main(String[] args) {new Thread(null, new Main(), "thread-1", 1024*1024*100).start();}@Overridepublic void run() {try{solve();}catch (Exception e){e.printStackTrace();}}private void solve(){Scanner cin = new Scanner(System.in);int n = cin.nextInt();long ans = 0;for(int i=1; i<n; i++) {int u = cin.nextInt(), v = cin.nextInt(), w = cin.nextInt();add(u, v, w);add(v, u, w);ans += 2 * w;}//两次dfs求树直径dfs(1, 0, 0);d = 0;dfs(deepest, 0, 0);//任取一点，树形dp//dfs(1, 0);System.out.println(ans - d);}private class Edge{int from, to, w;Edge(int from, int to, int w) {this.from = from;this.to = to;this.w = w;}}private void add(int from, int to, int w){if(g[from] == null){g[from] = new ArrayList<>();}g[from].add(new Edge(from, to, w));}//任取一点，树形dpprivate  void dfs(int root, int f){for(Edge e : g[root]){if(e.to != f){dfs(e.to, root);if(dp1[root] < dp1[e.to] + e.w){dp2[root] = dp1[root];dp1[root] = dp1[e.to] + e.w;}else{dp2[root] = Math.max(dp2[root], dp1[e.to]+e.w);}}}d = Math.max(d, dp1[root]+dp2[root]);}//两次dfs求树直径private void dfs(int root, int f, int dis){if(dis > d){d = dis;deepest = root;}for(Edge e : g[root]){if(e.to != f){dfs(e.to, root, dis + e.w);}}}
}

Java的HashMap比数组慢好多呀。。。。