卡方检验、F检验
- 定义
- χ 2 \chi^2 χ2 检验
- 1°
- 2°
- 3°
- 实验设计
- F F F 检验
- 1°
- 2°
- 3°
- 附录
- 假设检验一般步骤
- 势函数
定义
用于检验总体呈正态分布的方差的假设检验,其中 χ 2 \chi^2 χ2 检验常用于单样本正态方差检验; F F F 检验用于双样本的正态方差检验。
χ 2 \chi^2 χ2 检验、 F F F 检验不需要知道正态分布的均值,因为两者的检验准则、检验统计量都不包括 μ \mu μ。
另外, χ 2 , F \chi^2,F χ2,F 检验都是对正态分布非常敏感的。若总体不符合正态分布,则会大大影响检验的合理性。
χ 2 \chi^2 χ2 检验
χ 2 \chi^2 χ2检验的检验统计量为:
χ 2 = ( n − 1 ) s 2 σ 0 2 \chi^2=\frac{(n-1)s^2}{\sigma^2_0} χ2=σ02(n−1)s2
其中 s 2 s^2 s2 为样本方差, n n n 为样本容量, σ 0 2 \sigma_0^2 σ02 是与假设检验有关的常数。
以如下案例为例:
设总体 X X X 服从正态分布 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2), σ \sigma σ 未知。现从总体中抽出 n n n 个 i . i . d i.i.d i.i.d 的样品 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn,共同的分布为总体分布。
验证假设:
1 ∘ : H 0 : σ 2 = σ 0 2 H 1 : σ 2 ≠ σ 0 2 1^{\circ}:H_0:\sigma^2=\sigma_0^2~~~~H_1:\sigma^2\neq\sigma_0^2 1∘:H0:σ2=σ02 H1:σ2=σ02
2 ∘ : H 0 : σ 2 ≤ σ 0 2 H 1 : σ 2 > σ 0 2 2^{\circ}:H_0:\sigma^2\leq\sigma_0^2~~~~H_1:\sigma^2>\sigma_0^2 2∘:H0:σ2≤σ02 H1:σ2>σ02
3 ∘ : H 0 : σ 2 ≥ σ 0 2 H 1 : σ 2 < σ 0 2 3^{\circ}:H_0:\sigma^2\geq\sigma_0^2~~~~H_1:\sigma^2<\sigma_0^2 3∘:H0:σ2≥σ02 H1:σ2<σ02
1°
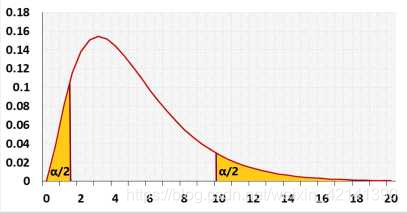
对于该双边检验,若 H 1 H_1 H1 为真,则检验统计量 χ 2 \chi^2 χ2 的倾向应是:
χ 2 > C 1 o r χ 2 < C 2 \chi^2>C_1~~or~~\chi^2<C_2 χ2>C1 or χ2<C2
根据假设检验的一般步骤:
给 定 显 著 水 平 α , ∵ χ 2 ↑ 或 χ 2 ↓ , H 0 越 难 成 立 , ⇓ 令 : P { χ 2 > C 1 o r χ 2 < C 2 ∣ H 0 } ≤ α 在 原 假 设 和 成 立 时 , χ 2 ∼ χ 2 ( n − 1 ) ⇓ C 2 = χ α / 2 2 ( n − 1 ) C 1 = χ 1 − α / 2 2 ( n − 1 ) ⇓ 求 得 拒 绝 域 为 χ 2 ∈ ( 0 , χ α / 2 2 ( n − 1 ) ) ∪ ( χ 1 − α / 2 2 ( n − 1 ) , + ∞ ) 给定显著水平 \alpha,\because \chi^2\uarr 或 \chi^2 \darr ,H_0 越难成立,\\ \Darr \\ 令:P\{ \chi^2>C_1~~or~~\chi^2<C_2|H_0\}\leq \alpha \\ ~\\ 在原假设和成立时,\chi^2\sim\chi^2(n-1)\\ \Darr\\ C_2=\chi^2_{\alpha/2}(n-1)\\ C_1=\chi^2_{1-\alpha/2}(n-1)\\ \Darr\\ 求得拒绝域为~ \chi^2\in(0,\chi^2_{\alpha/2}(n-1))\cup(\chi^2_{1-\alpha/2}(n-1),+\infin) 给定显著水平α,∵χ2↑或χ2↓,H0越难成立,⇓令:P{χ2>C1 or χ2<C2∣H0}≤α 在原假设和成立时,χ2∼χ2(n−1)⇓C2=χα/22(n−1)C1=χ1−α/22(n−1)⇓求得拒绝域为 χ2∈(0,χα/22(n−1))∪(χ1−α/22(n−1),+∞)
故只要求出检验统计量的观察值,根据拒绝域做出判断即可。
2°
跳转到假设定义
根据定义,检验统计量为:
χ 2 = ( n − 1 ) s 2 σ 0 2 \chi^2=\frac{(n-1)s^2}{\sigma_0^2} χ2=σ02(n−1)s2
根据假设检验的一般步骤:
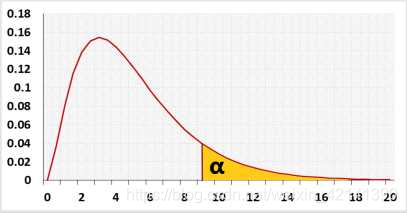
给 定 显 著 水 平 α , ∵ χ 2 ↑ , H 0 越 难 成 立 , ⇓ 故 令 : P { χ 2 = ( n − 1 ) s 2 σ 0 2 > C ∣ H 0 } ≤ α P { ( n − 1 ) s 2 σ 0 2 > C ∣ σ 2 ≤ σ 0 2 } ≤ α ⇓ P { ( n − 1 ) s 2 σ 2 > σ 0 2 C σ 2 ∣ σ 2 ≤ σ 0 2 } ⇓ ∵ P { ( n − 1 ) s 2 σ 2 > σ 0 2 C σ 2 ∣ σ 2 ≤ σ 0 2 } ≤ P { ( n − 1 ) s 2 σ 2 > C ∣ σ 2 ≤ σ 0 2 } ⇓ 而 当 σ 2 = σ 0 2 时 , χ 2 ∼ χ 2 ( n − 1 ) ⇓ C = χ 1 − α 2 ( n − 1 ) ⇓ 求 得 拒 绝 域 为 χ 2 ∈ ( χ 1 − α 2 ( n − 1 ) , + ∞ ) 给定显著水平 \alpha,\because \chi^2\uarr,H_0 越难成立,\\ \Darr \\ 故令:P\{ \chi^2=\frac{(n-1)s^2}{\sigma_0^2}>C|H_0\}\leq \alpha \\ ~\\ P\{\frac{(n-1)s^2}{\sigma_0^2}>C|\sigma^2\leq\sigma_0^2\}\leq \alpha \\ \Darr \\ P\{\frac{(n-1)s^2}{\sigma^2}>\frac{\sigma_0^2C}{\sigma^2}|\sigma^2\leq\sigma_0^2\}\\ \Darr\\ \because P\{\frac{(n-1)s^2}{\sigma^2}>\frac{\sigma_0^2C}{\sigma^2}|\sigma^2\leq\sigma_0^2\}\leq P\{\frac{(n-1)s^2}{\sigma^2}>C|\sigma^2\leq\sigma_0^2\}\\ \Darr\\ 而当 \sigma^2 = \sigma^2_0时,\chi^2\sim\chi^2(n-1)\\ \Darr\\ C=\chi^2_{1-\alpha}(n-1)\\ \Darr\\ 求得拒绝域为 \chi^2\in(\chi^2_{1-\alpha}(n-1),+\infin) 给定显著水平α,∵χ2↑,H0越难成立,⇓故令:P{χ2=σ02(n−1)s2>C∣H0}≤α P{σ02(n−1)s2>C∣σ2≤σ02}≤α⇓P{σ2(n−1)s2>σ2σ02C∣σ2≤σ02}⇓∵P{σ2(n−1)s2>σ2σ02C∣σ2≤σ02}≤P{σ2(n−1)s2>C∣σ2≤σ02}⇓而当σ2=σ02时,χ2∼χ2(n−1)⇓C=χ1−α2(n−1)⇓求得拒绝域为χ2∈(χ1−α2(n−1),+∞)
对于这类假设为单边,也称为单边(one-tailed)检验。单边检验的显著水平 α \alpha α,是对每个 μ \mu μ 都成立的上确界。而相反的,双边检验的原假设,往往对应一个值。
3°
跳转到假设定义
根据定义,检验统计量为:
χ 2 = ( n − 1 ) s 2 σ 0 2 \chi^2=\frac{(n-1)s^2}{\sigma_0^2} χ2=σ02(n−1)s2
根据假设检验的一般步骤:
给 定 显 著 水 平 α , ∵ χ 2 ↓ , H 0 越 难 成 立 , ⇓ 故 令 : P { χ 2 = ( n − 1 ) s 2 σ 0 2 < C ∣ H 0 } ≤ α P { ( n − 1 ) s 2 σ 0 2 < C ∣ σ 2 ≥ σ 0 2 } ≤ α ⇓ P { ( n − 1 ) s 2 σ 2 < σ 0 2 C σ 2 ∣ σ 2 ≥ σ 0 2 } ⇓ ∵ P { ( n − 1 ) s 2 σ 2 < σ 0 2 C σ 2 ∣ σ 2 ≥ σ 0 2 } ≤ P { ( n − 1 ) s 2 σ 2 < C ∣ σ 2 ≥ σ 0 2 } ⇓ 而 当 σ 2 = σ 0 2 时 , χ 2 ∼ χ 2 ( n − 1 ) ⇓ C = χ α 2 ( n − 1 ) ⇓ 求 得 拒 绝 域 为 χ 2 ∈ ( 0 , χ α 2 ( n − 1 ) ) 给定显著水平 \alpha,\because \chi^2\darr,H_0 越难成立,\\ \Darr \\ 故令:P\{ \chi^2=\frac{(n-1)s^2}{\sigma_0^2}<C|H_0\}\leq \alpha \\ ~\\ P\{\frac{(n-1)s^2}{\sigma_0^2}<C|\sigma^2\geq\sigma_0^2\}\leq \alpha \\ \Darr \\ P\{\frac{(n-1)s^2}{\sigma^2}<\frac{\sigma_0^2C}{\sigma^2}|\sigma^2\geq\sigma_0^2\}\\ \Darr\\ \because P\{\frac{(n-1)s^2}{\sigma^2}<\frac{\sigma_0^2C}{\sigma^2}|\sigma^2\geq\sigma_0^2\}\leq P\{\frac{(n-1)s^2}{\sigma^2}<C|\sigma^2\geq\sigma_0^2\}\\ \Darr\\ 而当 \sigma^2 = \sigma^2_0时,\chi^2\sim\chi^2(n-1)\\ \Darr\\ C=\chi^2_{\alpha}(n-1)\\ \Darr\\ 求得拒绝域为 \chi^2\in(0,\chi^2_{\alpha}(n-1)) 给定显著水平α,∵χ2↓,H0越难成立,⇓故令:P{χ2=σ02(n−1)s2<C∣H0}≤α P{σ02(n−1)s2<C∣σ2≥σ02}≤α⇓P{σ2(n−1)s2<σ2σ02C∣σ2≥σ02}⇓∵P{σ2(n−1)s2<σ2σ02C∣σ2≥σ02}≤P{σ2(n−1)s2<C∣σ2≥σ02}⇓而当σ2=σ02时,χ2∼χ2(n−1)⇓C=χα2(n−1)⇓求得拒绝域为χ2∈(0,χα2(n−1))
实验设计
在进行采样时,通常需要事前确定 n n n。
以 2° 为例,给定显著水平 α \alpha α, ∵ χ 2 ↑ , H 0 \because \chi^2\uarr,H_0 ∵χ2↑,H0 越难成立, ∴ \therefore ∴ 设定检验标准(拒绝)为: χ 2 > C \chi^2>C χ2>C。
定义势函数为:
为了书写方便,这里将自由度,移到下标去啦,大家见谅哈。。总不能一大推符号做下标吧
p ( μ ) = P { χ 2 > C ∣ σ 2 ∈ ( 0 , ∞ ) } = P { ( n − 1 ) s 2 σ 2 > σ 0 2 C σ 2 ∣ σ 2 ∈ ( 0 , + ∞ ) } ∵ ( n − 1 ) s 2 σ 2 ∼ χ n − 1 2 = 1 − χ n − 1 2 ( σ 0 2 C σ 2 ) \begin{aligned} p(\mu)&=P\{ \chi^2 > C| \sigma^2\in(0,\infin)\} \\ &= P\{ \frac{(n-1)s^2}{\sigma^2} > \frac{\sigma^2_0C}{\sigma^2}| \sigma^2\in(0,+\infin)\} \\ \because ~~&\frac{(n-1)s^2}{\sigma^2}\sim \chi^2_{n-1}\\ &=1-\chi^2_{n-1}(\frac{\sigma^2_0C}{\sigma^2}) \end{aligned} p(μ)∵ =P{χ2>C∣σ2∈(0,∞)}=P{σ2(n−1)s2>σ2σ02C∣σ2∈(0,+∞)}σ2(n−1)s2∼χn−12=1−χn−12(σ2σ02C)
取 α \alpha α,则根据检验标准的临界值求取法则,有:
s u p σ 2 { 1 − χ n − 1 2 ( σ 0 2 C σ 2 ) ∣ σ 2 ∈ ( 0 , σ 0 2 ) } < = α \underset{\sigma^2}{sup} \{1-\chi^2_{n-1}(\frac{\sigma^2_0C}{\sigma^2})|\sigma^2\in(0,\sigma^2_0)\} <= \alpha σ2sup{1−χn−12(σ2σ02C)∣σ2∈(0,σ02)}<=α
最后得到检验标准的临界值 C = χ n − 1 2 ( 1 − α ) C=\chi^2_{n-1}(1-\alpha) C=χn−12(1−α)
回代入势函数,可得:
p ( σ 2 ) = 1 − χ n − 1 2 ( σ 0 2 χ n − 1 2 ( 1 − α ) σ 2 ) p(\sigma^2) = 1-\chi^2_{n-1}(\frac{\sigma_0^2\chi^2_{n-1}(1-\alpha)}{\sigma^2}) p(σ2)=1−χn−12(σ2σ02χn−12(1−α))
其中有两个重要的性质:
- 势函数是 σ 2 \sigma^2 σ2 的函数,且是连续的、非减的。
- l i m σ 2 → σ 0 2 χ n − 1 2 ( σ 0 2 χ n − 1 2 ( 1 − α ) σ 2 ) = α l i m σ 2 → + ∞ χ n − 1 2 ( σ 0 2 χ n − 1 2 ( 1 − α ) σ 2 ) = 1 \underset{\sigma^2\to\sigma^2_0}{lim} \chi^2_{n-1}(\frac{\sigma_0^2\chi^2_{n-1}(1-\alpha)}{\sigma^2})=\alpha\\ \underset{\sigma^2\to+\infin}{lim}\chi^2_{n-1}(\frac{\sigma_0^2\chi^2_{n-1}(1-\alpha)}{\sigma^2})=1 σ2→σ02limχn−12(σ2σ02χn−12(1−α))=ασ2→+∞limχn−12(σ2σ02χn−12(1−α))=1
设无差别区域为 σ 2 ∈ ( σ 0 2 , Δ ) \sigma^2\in(\sigma^2_0,\Delta) σ2∈(σ02,Δ),则对于 [ Δ , + ∞ ] [\Delta,+\infin] [Δ,+∞],给定一个 β \beta β,使得 p ( σ 2 ) ≥ 1 − β p(\sigma^2)\geq1-\beta p(σ2)≥1−β。由于势函数是非减的,故问题转换为临界问题:
p ( σ 2 ) = 1 − χ n − 1 2 ( σ 0 2 χ n − 1 2 ( 1 − α ) σ 2 ) = 1 − β χ n − 1 2 ( σ 0 2 χ n − 1 2 ( 1 − α ) σ 2 ) = β \begin{aligned} p(\sigma^2) = 1-\chi^2_{n-1}(\frac{\sigma_0^2\chi^2_{n-1}(1-\alpha)}{\sigma^2}) = 1-\beta \\ \chi^2_{n-1}(\frac{\sigma_0^2\chi^2_{n-1}(1-\alpha)}{\sigma^2}) = \beta \end{aligned} p(σ2)=1−χn−12(σ2σ02χn−12(1−α))=1−βχn−12(σ2σ02χn−12(1−α))=β
从而得出适当的 n n n ,前者对应采样容量,后者是在测量问题上,可考虑提高测量精度。
其中, β \beta β 是当备选假设成立时,原假设被错误地接受的概率的临界值。
通过 β , α , Δ \beta,\alpha, \Delta β,α,Δ,即可知道我们进行试验设计,得出适当的 n n n 。
返回目录
F F F 检验
F F F 检验对总体是否正态非常敏感
F F F检验的检验统计量为:
F = s 1 2 s 2 2 F=\frac{s_1^2}{s_2^2} F=s22s12
其中 s 1 2 , s 2 2 s^2_1,s_2^2 s12,s22 为样本方差, X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2) X∼N(μ1,σ12),Y∼N(μ2,σ22)。
以如下案例为例:
设总体 X , Y X,Y X,Y 服从正态分布 N ( μ , σ 1 2 ) , N ( μ , σ 2 2 ) N(\mu,\sigma^2_1),N(\mu,\sigma^2_2) N(μ,σ12),N(μ,σ22), σ 1 , σ 2 \sigma_1,\sigma_2 σ1,σ2 未知。现从总体 X , Y X,Y X,Y 中分别抽出 n 1 n_1 n1 个 i . i . d i.i.d i.i.d 的样品 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn, n 2 n_2 n2个 i . i . d i.i.d i.i.d 样品 Y 1 , Y 2 , ⋯ , Y n Y_1,Y_2,\cdots,Y_n Y1,Y2,⋯,Yn ,共同的分布为总体分布 X , Y X, Y X,Y。
验证假设:
1 ∘ : H 0 : σ 1 2 = σ 2 2 H 1 : σ 1 2 ≠ σ 2 2 1^{\circ}:H_0:\sigma^2_1=\sigma_2^2~~~~H_1:\sigma^2_1\neq\sigma_2^2 1∘:H0:σ12=σ22 H1:σ12=σ22
2 ∘ : H 0 : σ 1 2 ≤ σ 2 2 H 1 : σ 1 2 > σ 2 2 2^{\circ}:H_0:\sigma_1^2\leq\sigma_2^2~~~~H_1:\sigma_1^2>\sigma_2^2 2∘:H0:σ12≤σ22 H1:σ12>σ22
3 ∘ : H 0 : σ 1 2 ≥ σ 2 2 H 1 : σ 1 2 < σ 2 2 3^{\circ}:H_0:\sigma_1^2\geq\sigma_2^2~~~~H_1:\sigma_1^2<\sigma_2^2 3∘:H0:σ12≥σ22 H1:σ12<σ22
返回目录
1°
对于该双边检验,若 H 1 H_1 H1 为真,则检验统计量 F F F 的倾向应是:
F > C 1 o r F < C 2 F>C_1~~or~~F<C_2 F>C1 or F<C2
根据假设检验的一般步骤:
给 定 显 著 水 平 α , ∵ F ↑ 或 F ↓ , H 0 越 难 成 立 , ⇓ 令 : P { F > C 1 o r F < C 2 ∣ H 0 } ≤ α 在 原 假 设 和 成 立 时 , s 1 2 / σ 1 2 s 2 2 / σ 1 2 = s 1 2 s 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) ⇓ C 2 = F α / 2 2 ( n − 1 ) C 1 = F 1 − α / 2 2 ( n − 1 ) ⇓ 求 得 拒 绝 域 为 F ∈ ( 0 , F α / 2 ( n − 1 ) ) ∪ ( F 1 − α / 2 ( n − 1 ) , + ∞ ) 给定显著水平 \alpha,\because F\uarr 或 F\darr ,H_0 越难成立,\\ \Darr \\ 令:P\{F>C_1~~or~~F<C_2|H_0\}\leq \alpha \\ ~\\ 在原假设和成立时,\frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_1^2}=\frac{s_1^2}{s_2^2}\sim F(n_1-1,n_2-1)\\ \Darr\\ C_2=F^2_{\alpha/2}(n-1)\\ C_1=F^2_{1-\alpha/2}(n-1)\\ \Darr\\ 求得拒绝域为~ F\in(0,F_{\alpha/2}(n-1))\cup(F_{1-\alpha/2}(n-1),+\infin) 给定显著水平α,∵F↑或F↓,H0越难成立,⇓令:P{F>C1 or F<C2∣H0}≤α 在原假设和成立时,s22/σ12s12/σ12=s22s12∼F(n1−1,n2−1)⇓C2=Fα/22(n−1)C1=F1−α/22(n−1)⇓求得拒绝域为 F∈(0,Fα/2(n−1))∪(F1−α/2(n−1),+∞)
 返回目录
返回目录
2°
跳转到假设定义
根据定义,检验统计量为:
F = s 1 2 s 2 2 F=\frac{s_1^2}{s_2^2} F=s22s12
根据假设检验的一般步骤:
给 定 显 著 水 平 α , ∵ F ↑ , H 0 越 难 成 立 , ⇓ 故 令 : P { F = s 1 2 s 2 2 > C ∣ H 0 } ≤ α P { s 1 2 s 2 2 > C ∣ σ 1 2 ≤ σ 2 2 } ≤ α ⇓ P { s 1 2 / σ 1 2 s 2 2 / σ 2 2 > σ 2 2 C σ 1 2 ∣ σ 1 2 ≤ σ 2 2 } ⇓ ∵ P { s 1 2 / σ 1 2 s 2 2 / σ 2 2 > σ 2 2 C σ 1 2 ∣ σ 1 2 ≤ σ 2 2 } ≤ P { s 1 2 / σ 1 2 s 2 2 / σ 2 2 > C ∣ σ 1 2 ≤ σ 2 2 } ⇓ 而 当 σ 1 2 = σ 2 2 时 , F ∼ F ( n 1 − 1 , n 2 − 1 ) ⇓ C = F 1 − α ( n 1 − 1 , n 2 − 1 ) ⇓ 求 得 拒 绝 域 为 F ∈ ( F 1 − α ( n 1 − 1 , n 2 − 1 ) , + ∞ ) 给定显著水平 \alpha,\because F\uarr,H_0 越难成立,\\ \Darr \\ 故令:P\{ F=\frac{s_1^2}{s_2^2}>C|H_0\}\leq \alpha \\ ~\\ P\{\frac{s_1^2}{s_2^2}>C|\sigma^2_1\leq\sigma_2^2\}\leq \alpha \\ \Darr \\ P\{\frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2}>\frac{\sigma_2^2C}{\sigma_1^2}|\sigma_1^2\leq\sigma_2^2\}\\ \Darr\\ \because P\{\frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2}>\frac{\sigma_2^2C}{\sigma_1^2}|\sigma_1^2\leq\sigma_2^2\}\leq P\{\frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2}>C|\sigma_1^2\leq\sigma_2^2\}\\ \Darr\\ 而当 \sigma_1^2 = \sigma^2_2时,F\sim F(n_1-1,n_2-1)\\ \Darr\\ C=F_{1-\alpha}(n_1-1,n_2-1)\\ \Darr\\ 求得拒绝域为 F\in(F_{1-\alpha}(n_1-1,n_2-1),+\infin) 给定显著水平α,∵F↑,H0越难成立,⇓故令:P{F=s22s12>C∣H0}≤α P{s22s12>C∣σ12≤σ22}≤α⇓P{s22/σ22s12/σ12>σ12σ22C∣σ12≤σ22}⇓∵P{s22/σ22s12/σ12>σ12σ22C∣σ12≤σ22}≤P{s22/σ22s12/σ12>C∣σ12≤σ22}⇓而当σ12=σ22时,F∼F(n1−1,n2−1)⇓C=F1−α(n1−1,n2−1)⇓求得拒绝域为F∈(F1−α(n1−1,n2−1),+∞)
 返回目录
返回目录
3°
跳转到假设定义
根据定义,检验统计量为:
F = s 1 2 s 2 2 F=\frac{s_1^2}{s_2^2} F=s22s12
根据假设检验的一般步骤:
给 定 显 著 水 平 α , ∵ F ↓ , H 0 越 难 成 立 , ⇓ 故 令 : P { F = s 1 2 s 2 2 < C ∣ H 0 } ≤ α P { s 1 2 s 2 2 < C ∣ σ 1 2 ≥ σ 2 2 } ≤ α ⇓ P { s 1 2 / σ 1 2 s 2 2 / σ 2 2 < σ 2 2 C σ 1 2 ∣ σ 1 2 ≥ σ 2 2 } ⇓ ∵ P { s 1 2 / σ 1 2 s 2 2 / σ 2 2 < σ 2 2 C σ 1 2 ∣ σ 1 2 ≥ σ 2 2 } ≤ P { s 1 2 / σ 1 2 s 2 2 / σ 2 2 < C ∣ σ 1 2 ≥ σ 2 2 } ⇓ 而 当 σ 1 2 = σ 2 2 时 , F ∼ F ( n 1 − 1 , n 2 − 1 ) ⇓ C = F 1 − α ( n 1 − 1 , n 2 − 1 ) ⇓ 求 得 拒 绝 域 为 F ∈ ( 0 , F 1 − α ( n 1 − 1 , n 2 − 1 ) ) 给定显著水平 \alpha,\because F\darr,H_0 越难成立,\\ \Darr \\ 故令:P\{ F=\frac{s_1^2}{s_2^2}<C|H_0\}\leq \alpha \\ ~\\ P\{\frac{s_1^2}{s_2^2}<C|\sigma^2_1\geq\sigma_2^2\}\leq \alpha \\ \Darr \\ P\{\frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2}<\frac{\sigma_2^2C}{\sigma_1^2}|\sigma_1^2\geq\sigma_2^2\}\\ \Darr\\ \because P\{\frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2}<\frac{\sigma_2^2C}{\sigma_1^2}|\sigma_1^2\geq\sigma_2^2\}\leq P\{\frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2}<C|\sigma_1^2\geq\sigma_2^2\}\\ \Darr\\ 而当 \sigma_1^2 = \sigma^2_2时,F\sim F(n_1-1,n_2-1)\\ \Darr\\ C=F_{1-\alpha}(n_1-1,n_2-1)\\ \Darr\\ 求得拒绝域为 F\in(0,F_{1-\alpha}(n_1-1,n_2-1)) 给定显著水平α,∵F↓,H0越难成立,⇓故令:P{F=s22s12<C∣H0}≤α P{s22s12<C∣σ12≥σ22}≤α⇓P{s22/σ22s12/σ12<σ12σ22C∣σ12≥σ22}⇓∵P{s22/σ22s12/σ12<σ12σ22C∣σ12≥σ22}≤P{s22/σ22s12/σ12<C∣σ12≥σ22}⇓而当σ12=σ22时,F∼F(n1−1,n2−1)⇓C=F1−α(n1−1,n2−1)⇓求得拒绝域为F∈(0,F1−α(n1−1,n2−1))
 返回目录
返回目录
附录
假设检验一般步骤
- 制定原假设、备选假设
- 制定检验统计量
- 取显著水平 α \alpha α,得出接受域、拒绝域
- [取 β \beta β,根据势函数得出 n n n]
- 判断检验统计量的观察值,所处的域,决定是否接受原假设
- [取 α , β \alpha, \beta α,β,根据势函数得出 n n n]
- 根据检验统计量的观察值,求出其 p-值,并据此做出决策
详见博文:假设检验
返回目录
势函数
势函数是包含了所有检验下,犯第一类错误的概率,和识别备选假设的能力。
详见博文:假设检验
返回目录