统计学之正态分布检验
本次主要是对数据集数据进行正态分布检验,数据集地址为:http://jse.amstat.org/datasets/normtemp.dat.txt
主要包括三列数据,体温(F)、性别(1:男,2:女)、心率(次/分钟)
1.数据统计
本次没有直接下载数据,而是手动将数据存储到本地了,应该可以直接下载数据到本地或者直接读取链接中的数据,有兴趣的可以自己动手试试。
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import requests
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats
##数据集http://jse.amstat.org/datasets/normtemp.dat.txt
data=pd.read_excel('F:\\temperature.xlsx')print(data.head(5))
L=data.ix[:,'体温'].values #读取所有行中‘体温’那一列
##print(L)
得到前5行数据
体温 性别 心率0 96.3 1 701 96.7 1 712 96.9 1 743 97.0 1 804 97.1 1 73
对温度数据的数据分布情况进行统计
print('平均值:',np.mean(L))
print('中位数:',np.median(L))
print('众数:',scipy.stats.mode(L))
print('标准差',np.std(L))
print('最大值',np.max(L))
print('最小值',np.min(L))
print('偏度:',scipy.stats.skew(L))
print('峰度',scipy.stats.kurtosis(L))
得到的结果为:
平均值: 98.24923076923078
中位数: 98.3
众数: ModeResult(mode=array([98.]), count=array([11]))
标准差 0.730357778905038
最大值 100.8
最小值 96.3
偏度: -0.004367976879198404
峰度 0.7049597854114715
2.数据展示
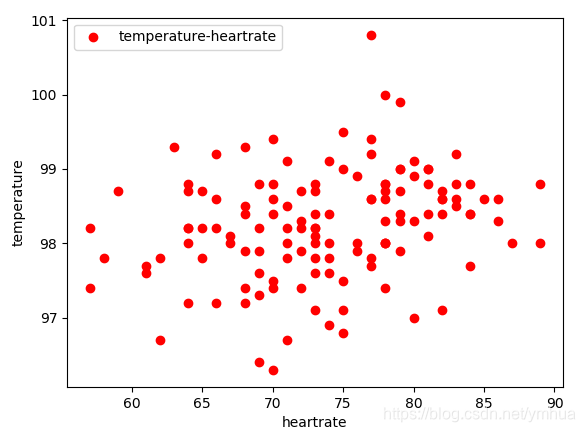
散点图
y=data.ix[:,'体温'].values #读取‘体温’那一列
x=data.ix[:,'心率'].values #读取‘心率'那一列
z=data.ix[:,'性别'].values #读取‘性别'那一列
plt.scatter(x,y,c='r',label='temperature-heartrate')
plt.legend()
plt.xlabel(u"heartrate")
plt.ylabel(u"temperature")
plt.show()
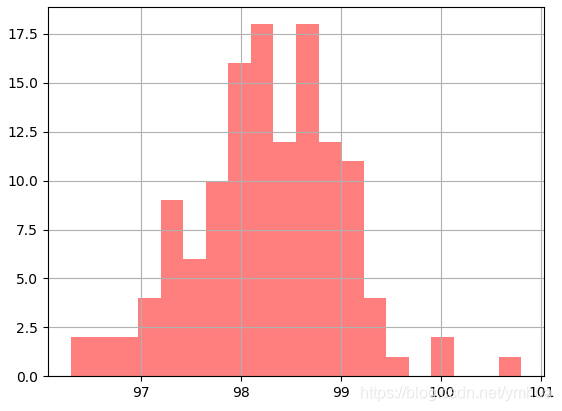
直方图和密度函数
#绘制体温直方图和密度函数
df=pd.DataFrame(L_tm)
df.hist(bins=20,alpha=0.5,color='r') #体温的直方图
df.plot(kind = 'kde', secondary_y=True) #体温的密度函数
plt.legend()
plt.show()
直方图
密度函数
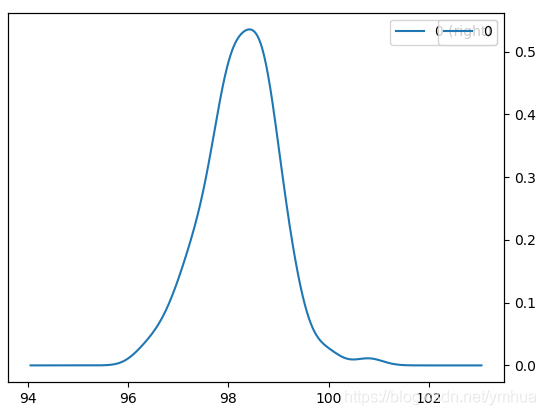
由直方图和密度函数可知体温基本符合正态分布。
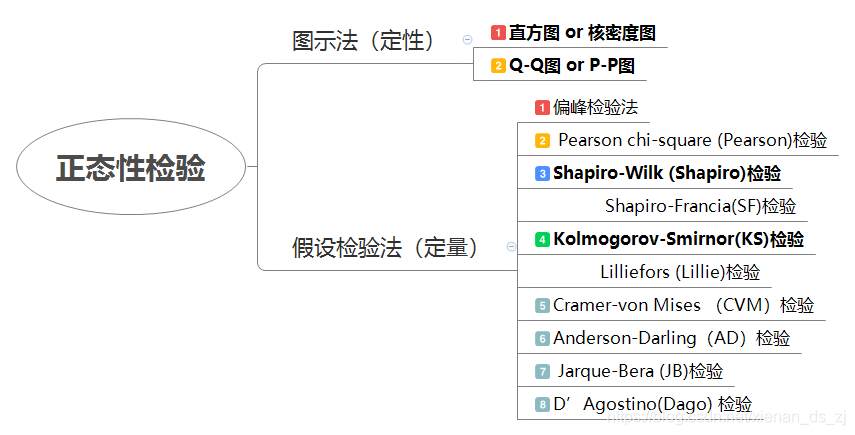
2.正态分布检验
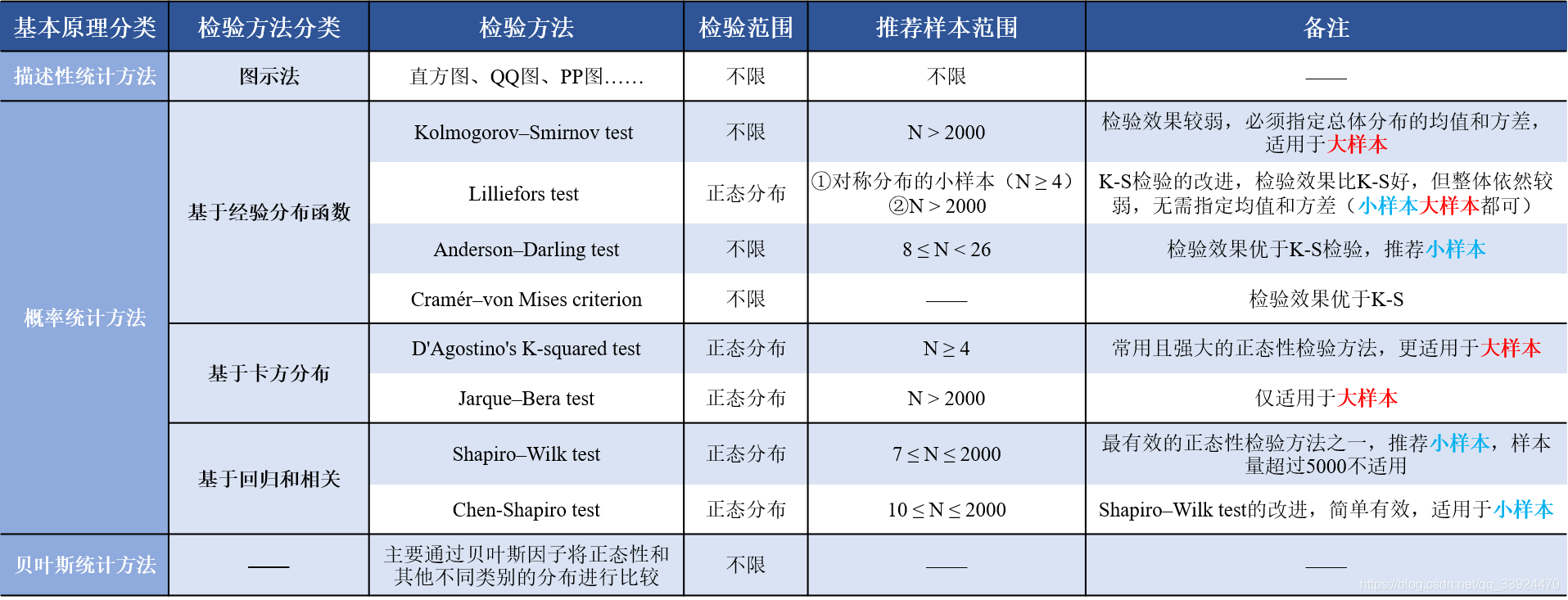
正态分布检验的方法有很多种,下面简单介绍几种。
(1)Shapiro-Wilk test
方法:scipy.stats.shapiro(x)
官方文档:SciPy v1.1.0 Reference Guide
参数:x - 待检验数据
返回:W - 统计数;p-value - p值
print('统计数和P-Value',scipy.stats.shapiro(L_tm))
统计数和P-Value (0.9865770936012268, 0.233174666762352)
P=0.23>0.05
(2)scipy.stats.kstest
方法:scipy.stats.kstest (rvs, cdf, args = ( ), N = 20, alternative =‘two-sided’, mode =‘approx’)
官方文档:SciPy v0.14.0 Reference Guide
参数:rvs - 待检验数据,可以是字符串、数组;
cdf - 需要设置的检验,这里设置为 norm,也就是正态性检验;
alternative - 设置单双尾检验,默认为 two-sided
返回:W - 统计数;p-value - p值
u=np.mean(L_tm)
std=np.std(L_tm)
print(scipy.stats.kstest (L_tm, 'norm', args = (u,std)))
KstestResult(statistic=0.06385348427883908, pvalue=0.6645320172840661)
3. Anderson-Darling test
方法:scipy.stats.anderson (x, dist =‘norm’ )
该方法是由 scipy.stats.kstest 改进而来的,可以做正态分布、指数分布、Logistic 分布、Gumbel 分布等多种分布检验。默认参数为 norm,即正态性检验。
官方文档:SciPy v1.1.0 Reference Guide
参数:x - 待检验数据;dist - 设置需要检验的分布类型
返回:statistic - 统计数;critical_values - 评判值;significance_level - 显著性水平
print(scipy.stats.anderson (L_tm, dist ='norm' ))
AndersonResult(statistic=0.5201038826714353, critical_values=array([0.56 , 0.637, 0.765, 0.892, 1.061]), significance_level=array([15. , 10. , 5. , 2.5, 1. ]))
(4)scipy.stats.normaltest
方法:scipy.stats.normaltest (a, axis=0)
官方文档:SciPy v0.14.0 Reference Guide
参数:a - 待检验数据;axis - 可设置为整数或置空,如果设置为 none,则待检验数据被当作单独的数据集来进行检验。该值默认为 0,即从 0 轴开始逐行进行检验。
返回:k2 - s^2 + k^2,s 为 skewtest 返回的 z-score,k 为 kurtosistest 返回的 z-score,即标准化值;p-value - p值
print(scipy.stats.normaltest (L_tm, axis=0))
NormaltestResult(statistic=2.703801433319236, pvalue=0.2587479863488212)
pvalue=0.26>0.05,因此体温服从正态分布