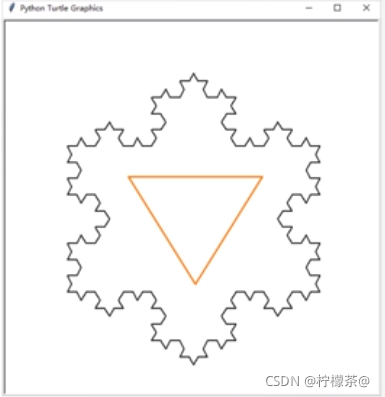
正态分布是很多计量数据比较分析的假设前提，因此在做比较分析之前要首先验证样本数据所代表的总体是否服从正态分布。当然对于比率数据的比较也需要满足分布前提，通常是二项分布和泊松分布，对于二项分布的比率比较，一般不需要做分布的验证。而对泊松分析的比率比较则需要事先验证其分布，验证方法就是卡方检验。

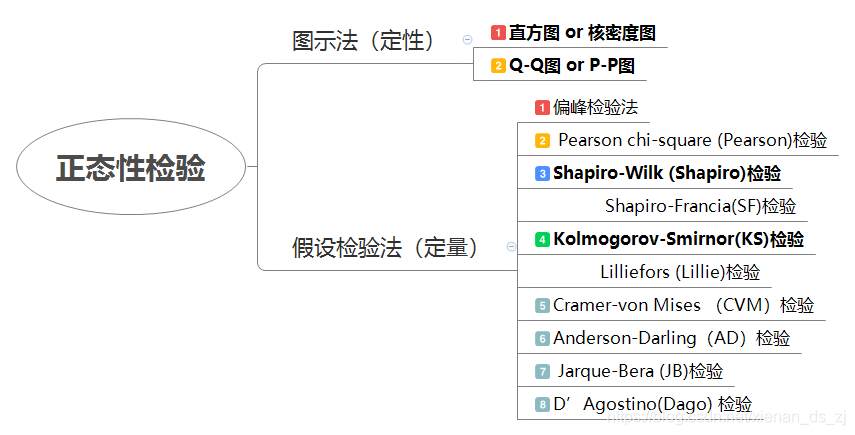
评价一元正态性的方法有大致分为以下几种：

1、图形验证

直方图
经验累积概率图（CDF）
QQ图

2、偏度和峰度

3、统计检验方法

常见的有以下几种

Kolmogorov-Smirnov检验
Cramer-von Mises检验
Anderson–Darling检验
Shapiro–Wilk检验

一、图形验证

优点：直观

缺点：1）、对于小样本并不适用；2）、图形方法以及下边的峰度偏度法只提供了一个粗糙而不正式的检验方法，没有一个明确的决定准则。

1、频率直方图

直方图需要注意的是数据的分区，对于小样本数据分区过大或过小画出来的直方图可能都会影响效果，可以多试几种分区，选择其中较好的分区效果。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import normdata=norm.rvs(loc=0,scale=1,size=1000) #生成1000个符合标准正态分布的浮点数。#返回的bins为列表，为频率分区                                                   
n, bins, patches=plt.hist(data,density=True, # true表示绘制的频率直方图总面积为1bins=20)  #默认分为10组，可以通过调节bins值，扩大分组。#计算样本的均值和标准差
mu=data.mean() 
sigma=data.std()#拟合一条最佳正态分布曲线y，y的值和分区bins的值对应
y = norm.pdf(bins, mu, sigma)
plt.plot(bins, y, 'r--') #绘制y的曲线

得到以下的频率直方图效果：

或者用seaborn绘制

import seaborn as sns 
sns.set_palette("hls") #设置所有图的颜色，使用hls色彩空间
sns.distplot(data,color="r",bins=20,kde=True)
plt.show()

输出：

我们知道，标准正态分布的数据，大致拟合一条“钟形”的曲线。

2、经验累积概率图

第二种要介绍的图是经验累积概率图，它的方法就是把数从小到大排列，求出每个值在总样本中出现的概率，如样本量是12，那么每个数出现的概率就是1/12=0.083。所谓累积，就是从小到大开始算起，前i个数加起来出现的概率，如前10个数的累积概率是0.83，画在图中就是这样的阶梯形的线。

import numpy as np
import statsmodels.api as sm # recommended import according to the docs
import matplotlib.pyplot as plt
import matplotlib.mlab as mlabplt.rcParams['font.sans-serif'] = ['FangSong']  # 设置默认字体
plt.rcParams['axes.unicode_minus'] = False   # 用于正常显示'-'负号
#sample = np.random.uniform(0, 1, 50) 
#非正态
#sample=np.array([1.7,2.8,1.4,2.6,-0.7,0.7,1.7,2.3,-28.00,2.4,0.0])
#正态
sample=np.array([9,18,13,0,5,-5,28,0,25,25,9,1])ecdf = sm.distributions.ECDF(sample) #累计密度概率#等差数列，用于绘制X轴数据
x = np.linspace(min(sample), max(sample)) #默认的个数为50个。
# x轴数据上值对应的累计密度概率
y = ecdf(x)
#绘制阶梯图
bins=plt.step(x, y,'b')mu=sample.mean()
sigma=sample.std()
#创建一个包含1000个元素的样本，提前设定均值和标准差
#loc表示均值
#scale表示标准差
#size表示个数
sample_normal=np.random.normal(loc=mu, scale=sigma, size=1000) 
ecdf_normal = sm.distributions.ECDF(sample_normal) #累计密度概率
#等差数列，用于绘制X轴数据
x_normal = np.linspace(min(sample_normal), max(sample_normal),1000) #默认的个数为50个。
# x轴数据上值对应的累计密度概率
y_normal = ecdf_normal(x_normal)
#绘制阶梯图
plt.plot(x_normal,y_normal,'r--')
plt.title('样本累计密度概率和正态累积概率密度')
plt.show()

图中红色的线是用样本均值和标准差画出来的理论曲线，它是用正态概率密度函数通过积分计算出来的。两条曲线对比，如果挨得很近，则数据正态的可能性就很大。

注意这种图不仅能够直观拟合正态曲线，也能拟合其它分布的曲线。

3、QQ图

标准正态分布是一条“钟形”的曲线； $t$ 分布同样也是呈现“钟形”，我们往往无法从频率分布直方图直接看出数据到底否服从正态分布呢？还是服从 $t$ 分布？为了方便比较，我们构建三种数据集，分别服从正态分布、指数分布以及 $t$ 分布，并绘制相应的直方图，图形如下：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import norm,t,lognorm,exponplt.rcParams['font.sans-serif']=['SimHei'] #用来显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data={}
data['标准正态分布']=norm.rvs(loc=0,scale=1,size=1000)    #生成1000个，满足（0,1）的标准正态分布
data['指数分布']=expon.rvs(scale=10,size=1000) #生成1000个服从（1/λ，1/λ）的指数分布，scale为1/λ,指数分布的均值和标准差都等于1/λ。
data['学生t分布']=t.rvs(df=5,loc=0,scale=1,size=1000)    #生成1000个服从t分布的数据,df表示学生t分布的自由度，详细可查询t分布和gamma分布的关系。fig=plt.figure(figsize=(12,3)) 
for i,(name,data_) in enumerate(data.items()):ax=fig.add_subplot(1,3,i+1) n, bins, patches=plt.hist(data_,label=name,density=True, # true表示绘制的频率直方图总面积为1bins=20) plt.title(name)  
plt.show()

注意： $t$ 分布的概率密度函数为： $f(t)=\frac{\Gamma (\frac{df+1}{2})}{\Gamma (\frac{df}{2})}(\frac{1}{\sqrt{df\pi }})^{2}[1+\frac{t^{2}}{df}]^{-(df +1)/2}$ ，其中 $df$ 表示自由度，更多 $t$ 分布和gamma分布的关系可见：《学生化t分布》，《统计学中,t分布中的自由度怎么解释？》。

数据分布可见下图：

可以看出 $t$ 分布比高斯（正态）分布有更长的尾巴（我们也叫其“厚尾”），也就是两边延伸得更开，这给出了 $t$ 分布的一个重要性质——鲁棒性，更长的尾巴意味着对于离群点能有更好的忍耐度，不会像高斯分布那样敏感。

接下来我们来画QQ图，我们知道，对样本数据标准化的公式为 $z=\frac{x-\mu }{\sigma }$ ，对其进行变形， $x=\sigma z+\mu$ ，若样本数据近似于正态分布，在QQ图上这些点近似的在直线 $x=\sigma z+\mu$ 上，此直线的斜率是标准差 $\sigma$ ，截距为均值 $\mu$ 。所以，利用QQ图可以作直观的正态性检验。若QQ图上的点近似的在一条直线上，可以认为样本数据来自正态总体。

绘制方法一：

#画图
plt.rcParams['font.sans-serif']=['SimHei'] #用来显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号fig=plt.figure(figsize=(12,3))x=np.array([-5,5])
for i,(name,data_) in enumerate(data.items()):ax=fig.add_subplot(1,3,i+1) mu=data_.mean() #样本均值sigma=data_.std()   #样本标准差y=sigma*x+mu plt.plot(x,y) #绘制截距为mu,斜率为sigma的直线xs=norm.rvs(loc=0,scale=1,size=len(data_))  #抽取等样本的标准正态值xs.sort()data_.sort()plt.scatter(xs,data_,color='r')  plt.xlabel('标准正态值')plt.ylabel('原始数据值')plt.title(name)
plt.show()

输出：

绘制方法二：

scipy中的stats有直接绘制QQ图的方法，如下：

from scipy import stats
fig=plt.figure(figsize=(12,3))
for i,(name,data_) in enumerate(data.items()):ax=fig.add_subplot(1,3,i+1) stats.probplot(data_, dist=stats.norm, plot=ax)plt.xlabel('标准正态值')plt.ylabel('原始数据值')plt.xlim(-4,4)plt.title(name)

输出：

根据QQ图的形状来判断正态性

直线 $\Rightarrow$ 正态
反“S”形 $\Rightarrow$ 比正态厚尾
“S”形 $\Rightarrow$ 比正态薄尾
凸弯曲 $\Rightarrow$ 右偏
凹弯曲 $\Rightarrow$ 左偏

二、数值验证

偏度讲的是分布的偏斜程度，偏度<0，代表分布有左偏；偏度=0，表示分布左右对称；偏度>0，表示分布有右偏，当然数值越大，偏斜程度也越大。

峰度讲的是分布的尖锐度，或者说是胖还是瘦。峰度<0，则分布比较胖；峰度为>0，则分布比较瘦。

对于一组数据来说，如果计算出来的偏度和峰度都在0附近，那么可以初步判断其分布服从正态分布。

python有计算数据偏度和峰度的函数，如下，对上面的数据集求各自的偏度，峰度。

for i,(name,data_) in enumerate(data.items()):data_s=pd.Series(data_)print('%s偏度：%s;峰度：%s。'%(name,data_s.skew(),data_s.kurt()))

输出：

标准正态分布偏度：-0.03483535284941679;峰度：0.008833727010514991。
指数分布偏度：1.930684125639356;峰度：4.741462640048853。
学生t分布偏度：0.845106666906179;峰度：5.391117437643347。

我们也可以调scipy中的stats()函数，计算不同分布下的偏度和峰度（输出的均为总体的分布，不是样本数据的分布）。

from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"norm.stats(loc=1,scale=2,moments='mvsk')    #正态分布。
expon.stats(scale=10,moments='mvsk')  #服从（1/λ，1/λ）的指数分布，scale为1/λ,指数分布的均值和标准差都等于1/λ。
t.stats(df=10000,loc=1,scale=2,moments='mvsk')    #t分布，df代表自由度，df越大，越接近正态分布。

输出：

(array(1.), array(4.), array(0.), array(0.))
(array(10.), array(100.), array(2.), array(6.))
(array(1.), array(4.00080016), array(0.), array(0.00060024))

四个参数分别代表均值、方差、偏度及峰度。

三、统计检验方法

以上验证的方法都属于直观检验，样本数据是否服从正态分布，还需要更加确切的检验。

常用的方法包括：

Kolmogorov-Smirnov检验
Cramer-von Mises检验
Anderson–Darling检验
Shapiro–Wilk检验

还有一些其它的检验方法，不一一列举了。

1、Kolmogorov-Smirnov检验

正态性检验，最直观的想法就是拿样本数据与期望的理论分布进行对比，如果差异不大，则可以认为数据服从正态分布，Kolmogorov-Smirnov检验（下边简称为“K-S检验”）方法就是这样的。

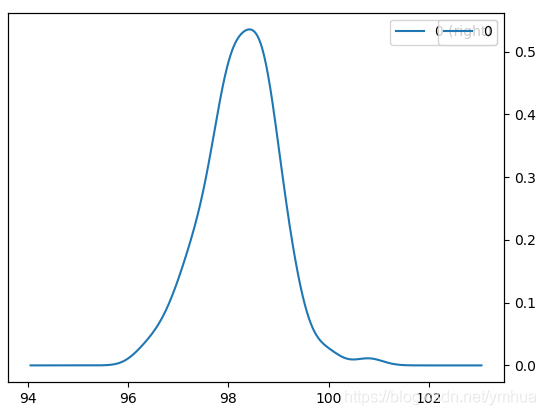
K-S检验找出在每一个数据点上经验累积概率与目标分布的累积概率之差的上界，列出公式是这样的：

$D_{n}=\sqrt{n}\sup_{x}\left | F_{n}(x)-F(x)\right |$

其中 $F_{n}(x)$ 代表样本数据的经验累积分布函数（cdf，上图中的蓝线）, $F(x)$ 代表与数据同均值、同方差的正态分布的累积分布函数（上图中的红线）。sup函数表示一组距离中的上确界，这是个数学概念，表示在原假设 $F_{n}(x)=F(x)$ 的条件下， $F_{n}(x)-F(x)$ 的绝对值的最小上界。其意图在于如果原假设成立，则 $D_{n}$ 应该很小，如果很大，则原假设不成立。

但是，这个上确界怎么求出来呢？请看下面的公式

其中k为样本从小到大排列后的序数。从公式中看出 $D_{n}$ 是经验和目标累积概率之差和错一位后再求出的差中最大的一个。

python实现

根据前面给的三个分布的数据，做K-S检验。

for i,(name,data_) in enumerate(data.items()):test_stat =stats.kstest(data_,'norm')print('%s：D统计量：%s;p_value值：%s。'%(name,test_stat[0],test_stat[1]))

输出：

标准正态分布：D统计量：0.030836687076312264;p_value值：0.2925276653484524。
指数分布：D统计量：0.8027309998111607;p_value值：0.0。
学生t分布：D统计量：0.0494681189296266;p_value值：0.014470853698413954。

由结果我们知道，取α=0.05（显著性水平），指数分布和学生t分布的的p_value值小于0.05，则拒绝原假设，即该分布不服从正态分布。

kstest 是一个很强大的检验模块，除了正态性检验，还能检验 scipy.stats 中的其他数据分布类型，仅适用于连续分布的检验。

kstest(rvs, cdf, args=(), N=20, alternative='two_sided', mode='approx', **kwds)

对于正态性检验，我们只需要手动设置三个参数即可：

rvs：待检验的一组一维数据
cdf：检验方法，例如'norm'，'expon'，'rayleigh'，'gamma'，这里我们设置为'norm'，即正态性检验
alternative：默认为双尾检验，可以设置为'less'或'greater'作单尾检验
model:'approx'(默认)，使用检验统计量的精确分布的近视值，'asymp'：使用检验统计量的渐进分布

注意：这种计算极差（理论和实际的最大差异）的方式，检验时对于样本量的要求较高，适合于大样本（一般 $\geq 2000$ ）数据的正态性检验。

2、Cramer-Von Mises检验（CVM检验）和Anderson–Darling检验（AD检验）

Cramer-Von Mises检验（CVM检验）

CVM检验的思想基本与K-S检验一致，与K-S检验相比，CVM检验统计量度量的是经验累积分布函数和目标累积分布函数的平方距离的积分。就是把每个数据点的差求平方以后相加，得到总的分布偏差，这样就考虑了所有的差异点，而不是像K-S检验那样只考虑一个最大的。如下图，其检验的统计量为：

$C=\int \left | F_{n}(x)-F(x)\right |^{2}dF(x)$

其中 $F_{n}(x)$ 代表样本数据的经验累积分布函数（cdf，上图中的蓝线）, $F(x)$ 代表与数据同均值、同方差的正态分布的累积分布函数（上图中的红线）。检验的过程：在原假设 $F_{n}(x)=F(x)$ 成立的条件下， $C$ 应该很小，如果 $C$ 很大，则原假设不成立。

Anderson–Darling检验（AD检验）

AD检验实际上是对CVM检验的一种改进，其检验的统计量为：

$A=\int \left | F_{n}(x)-F(x)\right |^{2}W(x)dF(x)=\int \frac{[F_{n}(x)-F(x) ]^{2}}{F(x)(1-F(x))}dF(x)$

AD检验实际上加上了一个权重函数 $W(x)=\frac{1}{F(x)(1-F(x))}$ ，这个权重，主要用于限制数据位置的权重，我们知道，如果数据落在左右两边的尾部位置，则 $F(x)(1-F(x))$ 会特别小，无限就近了0，则 $W(x)=\frac{1}{F(x)(1-F(x))}$ 会变大，相当于在计算尾部数据的平方距离时，给予了更高的权重；计算中间数据的平方距离时，给予其较小的权重。结合下边的图，我们认为这样设置是合理的。

3、Shapiro–Wilk检验（W检验）

K-S检验统计量用的是经验累积概率与目标理论累积概率之差的最大值，这有点像计算极差；AD检验则把所有的差平方后求和，有点像计算方差。当然计算方差的稳健性(Robustness)要好一些，这可能也是AD检验得到更多应用的原因。接下来我们再来介绍一种检验方法——W检验。

W检验的统计量是： $W=\frac{(\sum ^{n}_{i=1}a_{(i)}y_{(i)})^{2}}{\sum ^{n}_{i=1}(y_{i}-\overline{y})^{2}}$

$y_{(i)}$ 表示第 $i$ 个样本次序统计量，是从小到大排序后的数据。

$a_{(i)}$ 是标准正态分布中第 $i$ 个样本次序统计量标准化过后的值。即 $\sum ^{n}_{i=1}(a_{i}-\overline{a})^{2}=1$ 。

我们可以将此代入到上面的公式得： $W=\frac{(\sum ^{n}_{i=1}a_{(i)}y_{(i)})^{2}}{\sum ^{n}_{i=1}(a_{i}-\overline{a})^{2}\cdot \sum ^{n}_{i=1}(y_{i}-\overline{y})^{2}}$ ，此等式就类似我们求 $a_{(i)}$ 和 $y_{(i)}$ 的相关系数的公式。

可以把 $W$ 看作是顺序排列样本值 $y_{(i)}$ 和系数 $a_{(i)}$ 之间相关系数的平方(squared correlation coefficient)或者是线性回归的确定系数 $R^{2}$ (coefficient of determination $R^{2}$ for linear regression)，这个值最大为1，计算出的 $W$ 值越接近1，样本服从正态分布的可能性越大。当然也有判断的临界值，如果计算出的 $W$ 值大于临界值，则说明数据服从正态分布。

python实现

与 kstest 不同，shapiro 是专门用来做正态性检验的模块。

for i,(name,data_) in enumerate(data.items()):test_stat =stats.shapiro(data_)print('%s：W统计量：%s;p_value值：%s。'%(name,test_stat[0],test_stat[1]))

输出：

标准正态分布：W统计量：0.9982046484947205;p_value值：0.3791613280773163。
指数分布：W统计量：0.8033730387687683;p_value值：3.784428757365505e-33。
学生t分布：W统计量：0.9793980121612549;p_value值：1.0720994231272485e-10。

由结果我们知道，取α=0.05（显著性水平），指数分布和学生 $t$ 分布的的p_value值小于0.05，则拒绝原假设，即该分布不服从正态分布。

注意： $W$ 检验，精度较高，可适用于 $8\leq n\leq 50$ 的小样本数据，有其他统计学家把其适用范围扩展到5000，因此可以说 $W$ 检验几乎适用于所有的正态检验。正态性检验可优先考虑此方法。

了解更多正态性检验的推导，及如何选择合适的正态性检验可以见《经典比较篇之三：正态分布检验方法(二)》;《经典比较篇之四：正态分布检验方法(三)》。

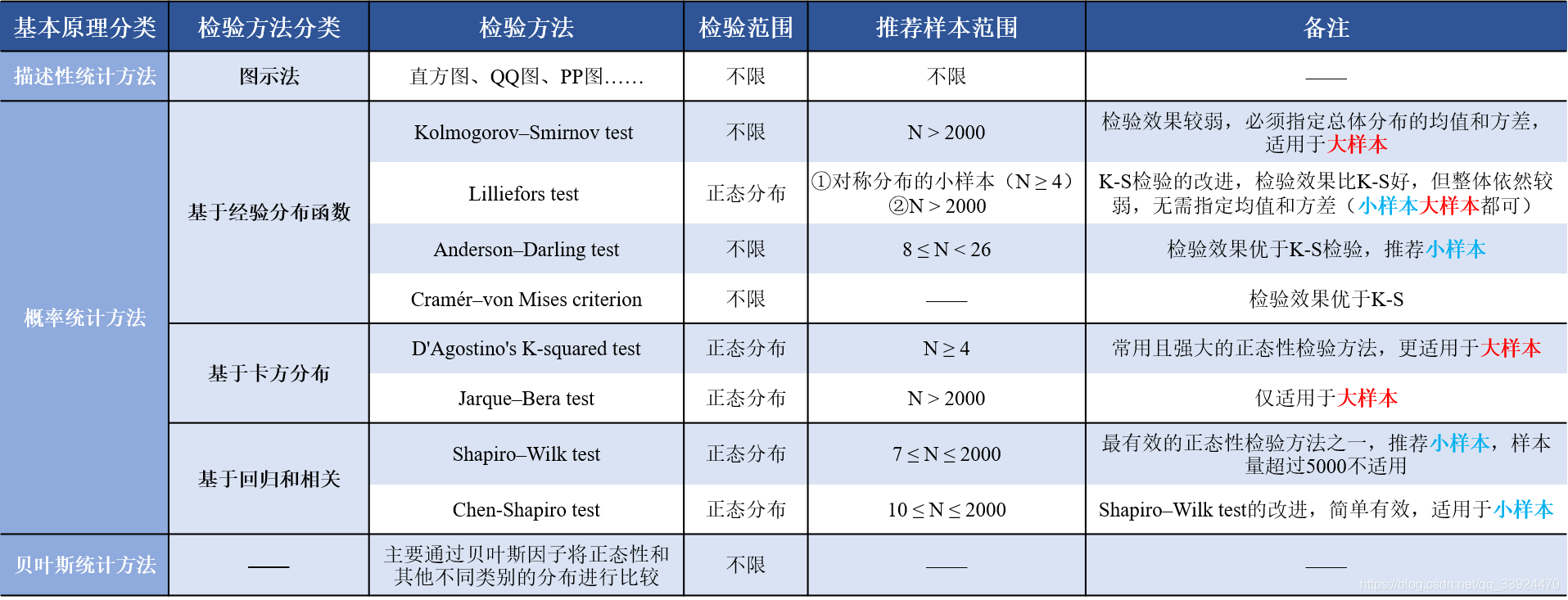
下边截取其文章中部分内容，说明各种正态检验方法该如何选择？

AD, RJ, 或KS: 哪一个正态检验最好?

前面介绍了几种常用的正态分布检验方法，可能会有很多人感到困惑，哪种方法最好呢？应该如何选择呢？理论上通常会进行功效上的对比，但实际应用上我们只关注哪个相对更好一些，我们可以做各种模拟试验来得出实际的结论，在这一点上已经有人做了，所以我就不费那个劲了，直接把别人的试验成功翻译出来，供大家参考。

Minitab软件提供了三种正态检验：Anderson-Darling (AD), Ryan-Joiner (RJ), and Kolmogorov-Smirnov (KS)。AD检验是缺省方法，但它是检验非正态的最佳方法吗？让我们比较一下在三种不同场景下这些检验正态的方法检验非正态数据的能力。我们用模拟的数据，但也基本反映了你在质量改进中分析数据时可能会碰到的常见情况。

场景1-制造过程会时不时会产生大的异常值，29个数模拟自均值=0，标准差=1的正态分布，1个数模拟自均值=0，标准差=4的正态分布。

场景2-制造过程发生了过程漂移，结果是分布上有平移。这产生了双峰的分布，均值之间有4个σ的差距，样本量为30。下图展示了两个正态分布之间均值存在的4个σ的差。

场景3-测量值实际服从非正态分布，典型的有失效时间和强度测量。本场景中，有30个数据模拟自Weibull分布(a=1，b=1.5)。

需要指出的是，三种场景并不是设计用来评估运用中心极限定理所做检验中正态假设的有效性，诸如1-样本、2-样本和配对t-检验。我们在这里关注在用一个分布来估计制造缺陷的概率时检验出非正态的情形。

在场景1，Ryan-Joiner检验是个明显的赢家，模拟结果见下图。

【译者注】纵坐标是拒绝正态的概率。

在场景2，Anderson-Darling检验最好，模拟结果如下。

在场景3，AD和RJ检验之间没什么不同。在检验非正态时两个都比Kolmogorov-Smirnov检验更有效。模拟结果如下。

总结一下，Anderson-Darling检验总不是最坏的检验，但在检验一个4σ的异常值时不像RJ检验那样有效。如果你要分析的制造过程数据有可能出现单个的异常值，Ryan-Joiner检验是最合适的。

RJ检验在两种场景中表现很好，但当数据存在漂移时检测非正态效果较差。如果你要分析的制造过程数据有可能由于未知的变化发生漂移，AD检验是最合适的。

KS检验在任何一种场景中都表现不好。

【译者注】因为博文中没有说明每个场景的模拟次数，所以模拟结论的可信性未知，另外这种模拟是否足够严谨也是值得考虑的一个方面，大家参考着用。下面是作者的另一篇博文，关注的是数据舍入后正态性检验的变化。

正态检验和舍入

Jim Colton， 2013.12.4

所有的测量值都有舍入。在很多情况下，你不希望仅仅因为数据有舍入而拒绝正态。实际上，如果实际的分布是正态的，那么正态分布是非常想要得到的数据模型，因为这样可以把有舍入的测量值带来的离散性弄得平滑一些。

有些正态检验在实际的分布服从正态时有非常大的比率因为舍入而拒绝(Anderson-Darling和Kolmogorov-Smirnov)，而另一些似乎能忽略掉舍入(Ryan-Joiner和卡方)。

我们来考察一个极端的例子，数据如何在完美服从正态分布的情况下得到拒绝的结论，比如从一个均值为10和标准差为0.14的正态分布中抽一个样本量为5000的样本。

下面的图展示了一部分舍入到小数点后两位的数据及其一个直方图和概率图。直方图和概率图看起来非常好。Ryan-Joiner通过了正态检验，其p值大于0.10(左边的概率图)。然而Anderson-Darling检验的p值小于0.005(右边的概率图)。很明显，在这个例子中拒绝正态是不合适的。

再模拟一个最常见的情况，n=30。模拟数据来自均值=0，标准差=1的正态分布，然后取整。下面就是这种模拟的一个例子。

在这种模拟的迭代过程中，Anderson-Darling的p值小于0.005，而Ryan-Joiner的p值大于0.10。

这种模拟的结果惊人地一致，Anderson-Darling检验几乎总是拒绝正态，Ryan-Joiner检验总是无法拒绝正态。模拟中也做了Kolmogorov-Smirnov和Chi-square检验。在避免因舍入而拒绝正态上，CS检验几乎与RJ检验一样的好。

第二个模拟考虑不那么极端的舍入(舍入的程度取决于测量分辨力/标准差，比例越大，舍入越极端)。模拟数据来自均值=0和标准差=2的正态分布，然后舍入到最近的整数。其中的一个例子见下图，在这种模拟的迭代中，Anderson-Darling的p值小于0.05，而Ryan-Joiner的p值大于0.10。

在第二个不太极端的舍入模拟中，AD和KS检验不那么经常拒绝了。

第三个模拟与第二个模拟的舍入程度相同，但样本量增大到n=100。由于样本量较大，AD和KS检验又回到了几乎总是拒绝的情况，RJ和CS检验也总是不因舍入而拒绝正态。

至此，我们只讨论了因舍入而拒绝正态的情况，但RJ和CS能检测到实际上是非正态的情况吗？最后一个模拟与第一个模拟的舍入程度相同，但取自实际上非正态分布。模拟数据来自标准差为1的指数分布，然后舍入到最近的整数。AD和KS检验正确地拒绝正态，但可能是因为舍入，也可能是因为非正态。RJ和CS也能检验到非正态，但不像AD和KS那样频繁。