2.5 总体分布正态性检验

进行参数估计和假设检验时，通常总是假定总体服从正态分布，虽然在许多情况下这个假定是合理的，但是当要以此为前提进行重要的参数估计或假设检验，或者人们对它有较大怀疑的时候，就确有必要对这个假设进行检验，

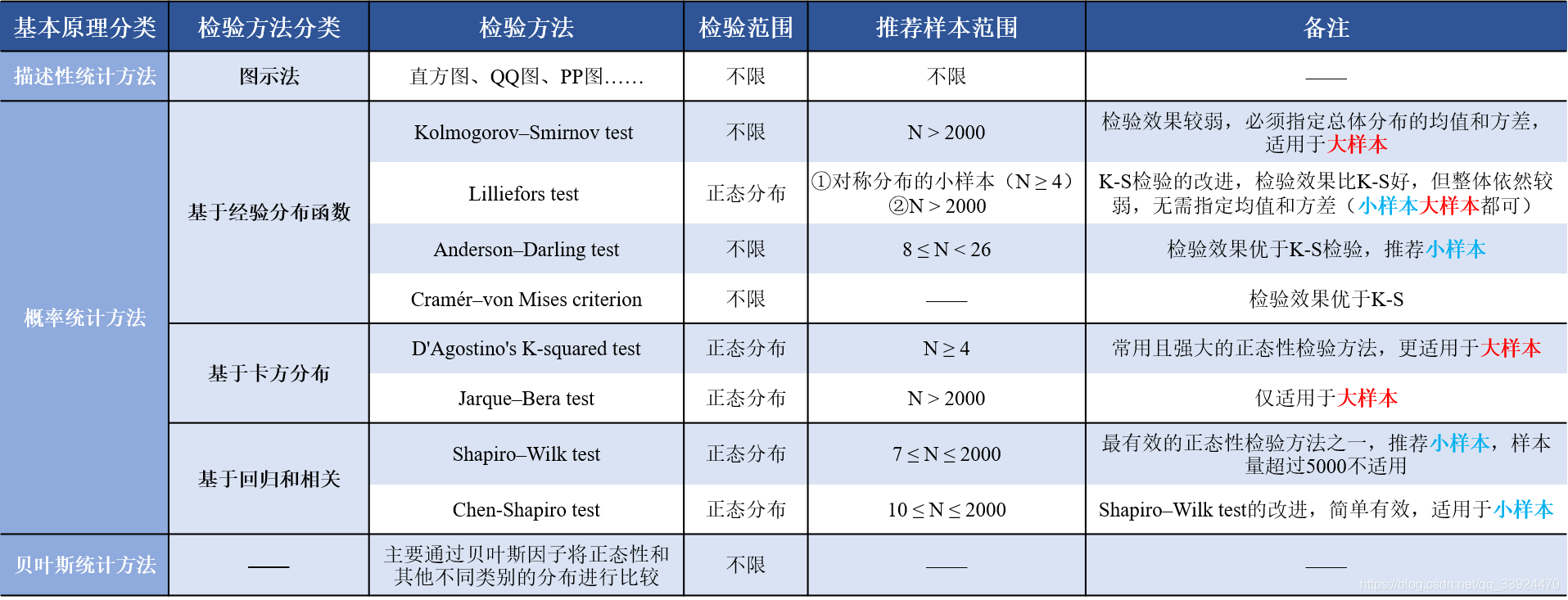
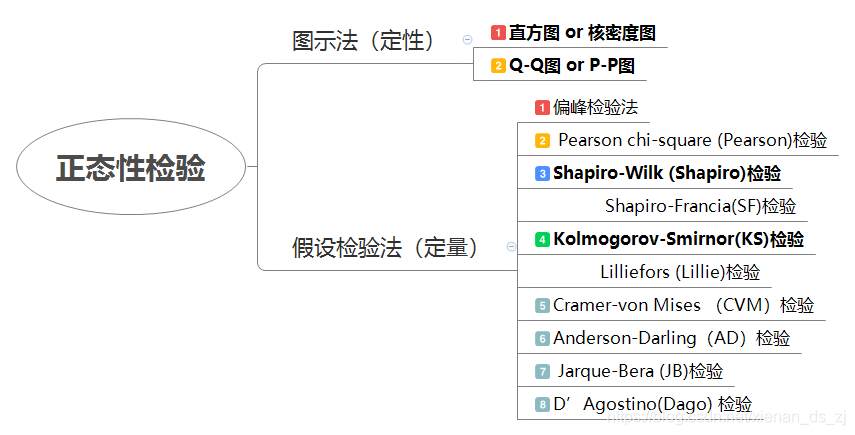
进行总体正态性检验的方法有很多种，以下针对MATLAB统计工具箱中提供的程序，简单介绍几种方法。

1)Jarque-Bera检验

利用正态分布的偏度g1和峰度g2，构造一个包含g1，g2的分布统计量(自由度n=2)，对于显著性水平，当分布统计量小于分布的分位数时，接受H0：总体服从正态分布；否则拒绝H0，即总体不服从正态分布。这个检验适用于大样本，当样本容量n较小时需慎用。Matlab命令：h

=jbtest(x)，[h,p,jbstat,cv] =jbtest(x,alpha)。

2)Kolmogorov-Smirnov检验

通过样本的经验分布函数与给定分布函数的比较，推断该样本是否来自给定分布函数的总体。容量n的样本的经验分布函数记为Fn(x)，可由样本中小于x的数据所占的比例得到，给定分布函数记为G(x)，构造的统计量为，即两个分布函数之差的最大值，对于假设H0：总体服从给定的分布G(x)，及给定的，根据Dn的极限分布(n®¥时的分布)确定统计量关于是否接受H0的数量界限。

因为这个检验需要给定G(x)，所以当用于正态性检验时只能做标准正态检验，即H0：总体服从标准正态分布。Matlab命令：h =kstest(x)。

3)Lilliefors检验

它将Kolmogorov-Smirnov检验改进用于一般的正态性检验，即H0：总体服从正态分布，其中由样本均值和方差估计。Matlab命令：

h

=lillietest(x)，[h,p,lstat,cv]=lillietest(x,alpha)。

4)另外还有一种方法：首先对于数据进行标准化：Z =

ZSCORE(X)，然后在进行2)的Kolmogorov-Smirnov检验，检验是否为标准正态分布，类似于对于方法2)的改进

=================================================================

SPSS中做正态分布检验的方法比较简单，利用具体操作过程如下，

Analyze==>Nonparametic

test==>1-sample K-S

可以检验正态分布，均匀分布，泊松分布和指数分布

结果如下

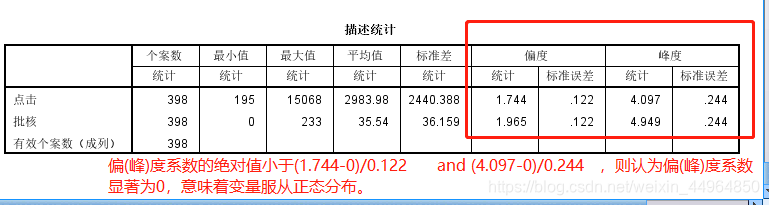
零假设为：样本来自得总体服从正态分布，如果检验显著性水平大于0.05，则不能拒绝零假设，即服从正态分布，反之，如果检验显著性水平小于0.05，那么拒绝零假设，即不服从正态分布。

======================================================================================

还有别的方法，可以参考：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

附带四种检验的解释：

lillietest

函数检验正态性，其实质就是先用样本估计正态分布的参数，然后做 K-S 检验

ttest函数是用来做方差未知时单个正态总体均值的检验，前提是总体服从正态分布，而不是检验数据是否服从正态分布。