前言

在科学研究中，往往需要对数据进行差异性检验，而常用的参数检验需要数据服从正态分布，因此在决定是否采用参数检验之前需要先对数据进行正态性检验。这一步在任何统计学软件中（如SPSS、SAS、Origion、GraghPad等）都能够轻易实现，但每个软件都会同时包括多种正态检验方法，此时该选哪个方法来对自己的数据进行正态性检验呢？这就是本文要解决的主要问题。在查阅相关资料后，本文将对多种常见的正态检验方法进行简单地归纳总结，尽可能写清楚每个检验方法的适用范围，但对于每个检验方法的数学统计学原理不作深入解析，仅简略描述其大致的基本原理。

在统计学中，正态检验主要用于检验一个数据集是否服从正态分布。常用的t检验、方差分析（ANOVA）等参数检验都有一个共同的前提条件：样本数据必须服从正态分布，即样本数据必须来源于一个正态分布的总体，若样本数据不服从正态分布，就不能用以上参数检验对数据进行分析，而应该使用非参数检验（如卡方检验、置换检验等）。因此在对数据进行统计分析之前，第一步就需要对数据进行正态性检验，以检验该数据来自正态分布总体的概率有多大，再选择对应的参数或非参数检验方法进行分析。

一、正态检验基本原理概述

正态检验属于非参数检验，其检验方法有很多种，且每一种检验方法的基本原理和适用条件都有所不同。在所有正态性检验方法中，其基本原理主要可以从以下三个方面进行解释：

（1）从描述性统计方法的角度来说，要检验数据是否服从正态分布，可以计算“数据分布”和“标准正态分布模型”之间的拟合优度，若拟合性较差，即认为数据不服从正态分布；

（2）从概率统计方面，即假设检验的角度来说，数据是否服从正态分布可以通过与“数据服从正态分布”这样一个零假设进行假设检验计算，构建相关统计量来计算出检验结果；

（3）从贝叶斯统计的角度来说，该方法本身并不检验其正态性，而是计算这批数据来自于服从μ、σ正态分布总体的可能性更大，还是来自于其他分布总体的可能性更大。

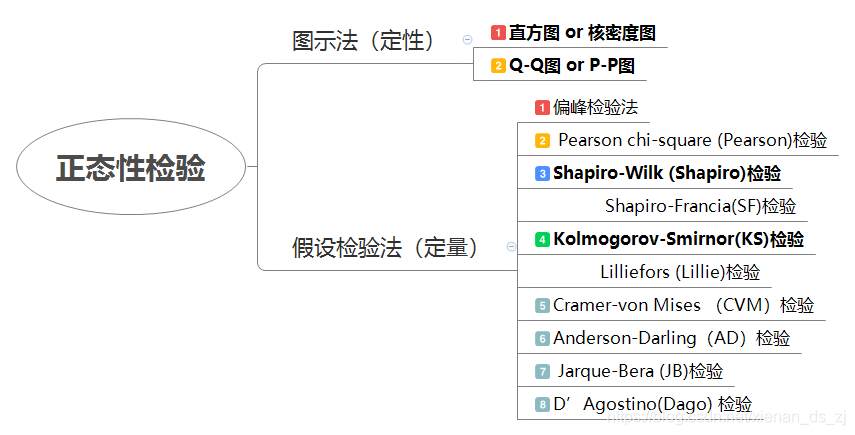
二、正态检验方法汇总与简述

根据以上三个不同角度的基本原理，可以把正态检验方法分为以下三部分：

1、描述性统计方法

描述性统计方法实际上就是图示法。该方法直接通过绘制数据的直方图，与标准正态分布曲线进行比较。但该方法在数据量少的时候比较难看出两者之间的差异，因此更多地会通过对数据直方图曲线与对应μ、σ的标准正态分布曲线之间进行回归，计算出拟合优度来说明两条曲线之间的拟合程度。这种用于评估数据正态性的图形工具有很多，其中“分位数-分位数图”（quantile-quantile plot，QQ plot），即QQ图是正态检验中最常见的图示方法。这种图正是样本数据直方图和正态分布图之间一种拟合优度的直观度量方式，当QQ图上的点都大致落在一条直线上时，表示高度正相关，即这些数据是正态分布的。

除此以外，不同的统计软件还会提供一些其他的正态检验图示方法，如直方图、PP图等。（PP图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图，用于直观地检测样本数据是否符合某一概率分布。如果被检验的数据符合所指定的分布，则代表样本数据的点应当基本在代表理论分布的对角线上。）

图示法相关链接：

正态QQ图原理

PP图和QQ图

2、概率统计方法

概率统计方法是最常用也是种类最多的正态检验方法，主要包括以下三类。（仅列举常用的部分方法，还有许多其他较新的检验方法及现有检验方法的改进方法等均未列出。）

（1）基于经验分布函数（empirical distribution function,EDF）

①Kolmogorov–Smirnov test

简称为K-S检验, 是最为常用的正态性检验方法之一，其方法主要是计算出经验分布和理论分布之间的距离，并将其中最大的距离（差异）作为检验统计量。因此K-S检验的优点是不仅可检验正态分布，还可用于检验其他任何分布。但K-S检验需要我们已经事先知道分布总体的均值和方差，即需要指定总体的均值和方差才能进行计算，但在实际情况下很少会事先知道总体的均值和方差，所以难以进行K-S检验。同时也因为仅仅把分布间的最大差异作为统计量，因此相比于其他检验方法其敏感性相对弱一些，因此在GraphPad软件中不推荐使用该方法来进行正态性检验，但实际上在大样本情况下K-S检验还是非常实用的（SAS推荐样本量>2000）。

②Lilliefors test

该检验实际上是K-S检验的一种改进方法（可简写成K-S-L检验），计算方法比K-S更复杂一些，主要通过计算经验分布函数与累积分布函数之间的最大差异来进行检验，还包括对K-S检验的P值进行了调整等等，另外K-S-L检验直接利用样本的均值和方差进行计算，因此不需要事先指定总体分布的均值和方差。因此相比于K-S检验，K-S-L的检验效果更好一些，但与其他检验方法相比其敏感性依然较弱。在GraphPad中的K-S检验为了不需要用户指定总体分布的均值和方差，实际上采用的是K-S-L检验。另外，K-S-L检验最适用于对称分布的小样本（origion、matlab），同时也适用于大样本（origion中提到大样本分布曲线间的最大差异更具有统计显著性，因此一些分析人士建议K-S-L的样本量最好大于2000），但只适用于正态性检验。

③Anderson–Darling test

简称为A-D检验，该检验主要通过计算数据的累积分布曲线与理想正态分布的累积分布曲线之间的差异来进行检验，与K-S检验不同，该方法考虑了两条累积分布曲线之间的所有差异，因此它比K-S检验效果更好，也是检验正态性最好的方法之一。但该方法的缺点是仅适用于小样本，Origion中推荐样本量为26个以下，但有些超过200的工业数据也有可能通过A-D检验，另外该方法还可用于检验其他分布。

④Cramér–von Mises criterion

（较少用，不作详细说明。SAS软件有提供该检验。）

（2）基于卡方分布（Chi-squared distribution）

①D'Agostino's K-squared test （Skewness-Kurtosis test）

该方法主要通过计算偏度（Skewness）和峰度（Kurtosis）来量化数据分布曲线与标准正态分布曲线之间的差异与不对称性，然后计算这些值与正态分布期望值的之间的不同程度。D'Agostino's K-squared test是一种常用且强大的正态性检验方法，是GraphPad中推荐的正态检验方法。由于分布曲线的偏度和峰度容易受到数据量的影响，因此该方法适用于大样本，且仅能用于正态性检验。

②Jarque–Bera test

该方法通过计算样本数据和正态分布两者偏度与峰度的拟合优度，来检验样本是否来自均值和方差均未知的正态分布（即零假设中的正态分布参数是未知的，是一种双侧拟合优度检验）。Jarque–Bera test通常使用卡方分布来估计大样本的临界值，该临界值是通过蒙特卡洛模拟（Monte Carlo）计算出来的，因此该方法必须用于大样本（matlab提到样本量小于2000时，显著性水平会从0.001跌到0.5），且只能用于正态性检验。

（3）基于回归和相关（regression- and correlation-based）

①Shapiro–Wilk test

Shapiro–Wilk test是正态性检验最为有效的方法之一，是一种在频率统计中检验正态性的方法，但其测试基础较难理解（不多加叙述）。该方法在每一个样本值都是唯一时的检验效果最好，但若样本中存在几个值重复的情况下该方法便会大打折扣。因此该方法只适用于小样本，推荐样本量为7~2000，Origion中允许样本大小为3~5000，当样本量超过5000时不再适用。该方法仅适用于正态性检验。

②Chen-Shapiro test

Chen-Shapiro test是在不损失功率的情况下，Shapiro-Wilk test的拓展，是一个相对简单又有效的正态检验方法，和Shapiro-Wilk test一样只适用于小样本（<2000），同时仅适用于正态性检验。

③Ryan-Joiner test

（较少用，不作详细说明。）

④Shapiro-Francia test

（较少用，不作详细说明。）

在不同的统计软件（如SPSS、R、SAS、origion、GrapgPad等）中，会包括其中几个不同的正态检验方法，具体请查看相关软件的说明书。

3、贝叶斯统计方法

主要通过贝叶斯因子将正态性和其他不同类别的分布进行比较。

三、正态检验方法总结（太长不看版）

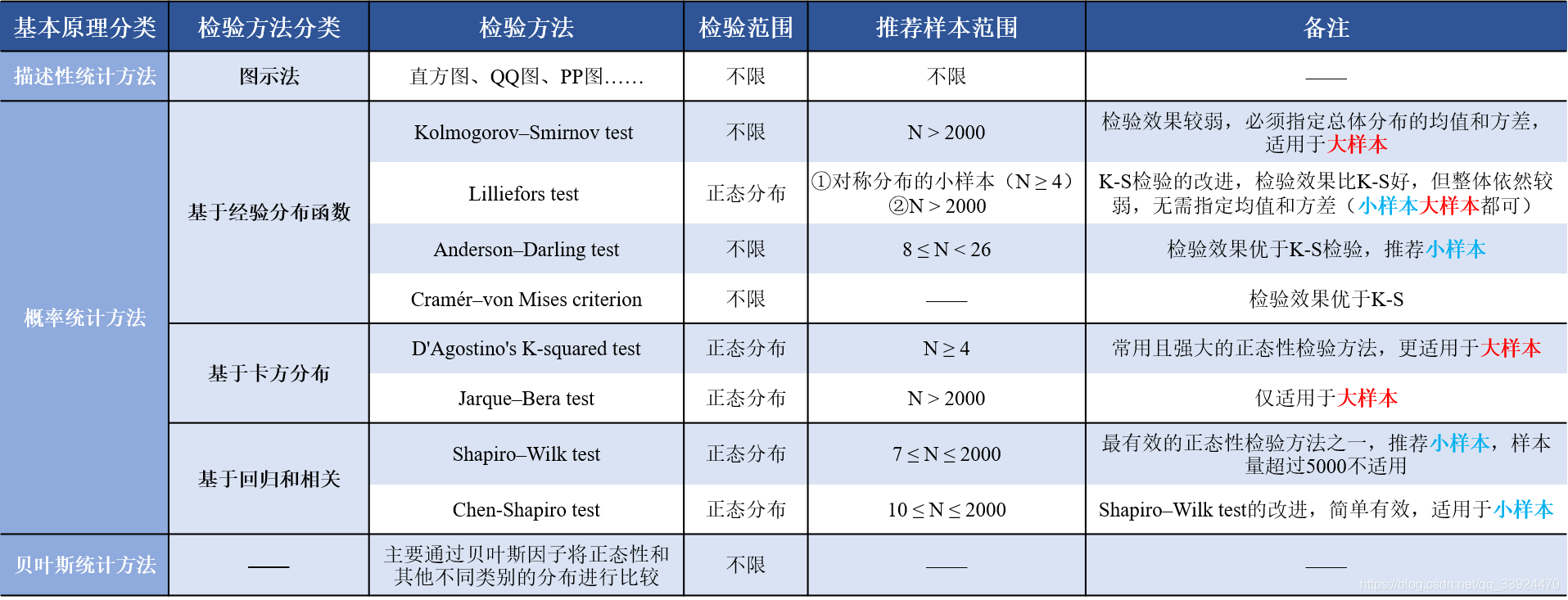
根据查阅相关资料和软件说明书，以下为正态性检验的常用选择方法：

（1）当样本量较大时通常会选择 K-S-L test 或 D'Agostino's K-squared test

（2）当样本量较小时通常选用 Anderson-Darling test 或 Shapiro-Wilk test

当然具体还是要根据数据本身以及相关文献的处理方法进行选择！！！

四、关于正态检验的其他问题

（1）由于每个正态性检验方法的检验角度不同，因此同一批数据用不同的检验方法可能得到的结果会不尽相同，所以在实际操作中可以根据样本量大小选择多种检验方法进行正态性检验，同时通过QQ图等图示法辅助判断；

（2）正态性检验只是检验样本数据来自正态分布总体的可能性有多大，或者说只是检验样本数据的总体是否近似正态分布，因此样本的总体并不是一定服从标准正态分布，但已有大量实验表明，即使总体仅为近似的正态分布，也能很好地进行 t -test、方差分析等参数检验。

（3）有些样本的总体可能仅为近似的正态分布，但没有一种直接的方法可以决定“偏离正态性的严重程度”是否足以改变“进行参数检验”的选择。正态性检验的意义本身并不全是为了决定什么时候使用非参数检验，还包括在确定一个样本的总体如果近似服从正态分布后，可以使用更加简单的方法来制定参考值范围、对数据进行质量控制等等。决定使用参数检验还是非参数检验是一个非常复杂且困难的问题，在实际研究中，不应该仅基于正态性检验的结果来自动断定是否使用非参数检验，还需要根据实际问题更深入地考虑其他影响因素（具体问题具体分析）。

（4）正态性检验在大多数情况下并不是十分有用。因为在样本量很少的情况下，正态检验对于检测“非正态分布”的作用不是很大；而当样本量足够大的时候，数据是否需要严格通过正态性检验、是否需要严格服从正态分布就显得不那么重要了，因为t 检验和方差分析等对于近似正态分布数据的检测结果是非常稳定的（根据大数定律和中心极限定理，当样本量足够大时，所有分布都近似于正态分布）。因此正态性检验只是一个测试方法，用于告诉我们自己的数据偏离理想正态分布的情况是否严重到足以使以正态分布为前提条件的统计方法失效，正态性检验的结果只是一个参考。