ec java sm2证书_国密算法SM2证书制作

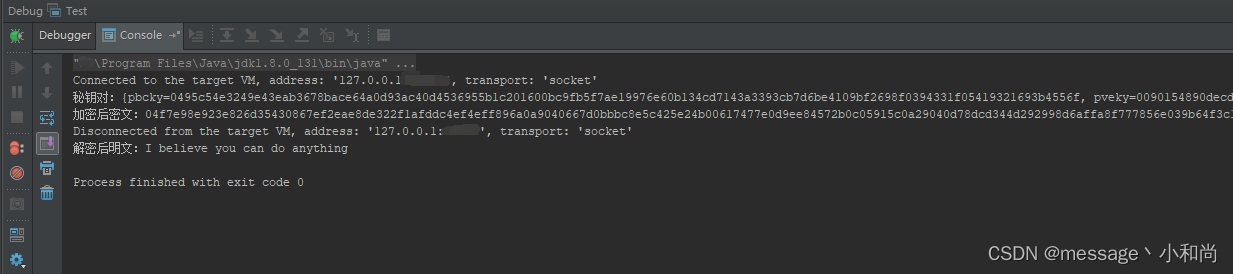
前段时间将系统的RSA算法全部升级为SM2国密算法，密码机和UKey硬件设备大都同时支持RSA和SM2算法，只是应用系统的加解密签名验证需要修改，这个更改底层调用的加密动态库来，原来RSA用的对称加密算法DES(AES)和摘要MD5(SHA1)也相应改变，分别对应SM1、SM3算法，SM1算法基于硬件实现，SM2、SM3算法已公开。

SM2签名验证算法

SM2签名同样也是需要先摘要原文数据，即先使用SM3密码杂凑算法计算出32byte摘要。SM3需要摘要签名方ID(默认1234567812345678)、曲线参数a,b,Gx,Gy、共钥坐标(x,y)计算出Z值，然后再杂凑原文得出摘要数据。这个地方要注意曲线参数和坐标点都是32byte，在转换为BigInteger大数计算转成字节流时要去掉空补位，否则可能会出现摘要计算不正确的问题。SM2签名实现如下：

public static BigInteger[] Sm2Sign(byte[] md, AsymmetricCipherKeyPair keypair)

{

SM3Digest sm3 = new SM3Digest();

ECPublicKeyParameters ecpub = (ECPublicKeyParameters)keypair.Public;

byte[] z = SM2CryptoServiceProvider.Sm2GetZ(Encoding.Default.GetBytes(SM2CryptoServiceProvider.userId), ecpub.Q);

sm3.BlockUpdate(z, 0, z.Length);

byte[] p = md;

sm3.BlockUpdate(p, 0, p.Length);

byte[] hashData = new byte[32];

sm3.DoFinal(hashData, 0);

// e

BigInteger e = new BigInteger(1, hashData);

// k

BigInteger k = null;

ECPoint kp = null;

BigInteger r = null;

BigInteger s = null;

BigInteger userD = null;

{

ECPrivateKeyParameters ecpriv = (ECPrivateKeyParameters)keypair.Private;

k = ecpriv.D;

kp = ecpub.Q;

userD = ecpriv.D;

// r

r = e.Add(kp.X.ToBigInteger());

r = r.Mod(ecc_n);

}

while (r.Equals(BigInteger.Zero) || r.Add(k).Equals(ecc_n));

// (1 + dA)~-1

BigInteger da_1 = userD.Add(BigInteger.One);

da_1 = da_1.ModInverse(ecc_n);

// s

s = r.Multiply(userD);

s = k.Subtract(s).Mod(ecc_n);

s = da_1.Multiply(s).Mod(ecc_n);

}

while (s.Equals(BigInteger.Zero));

byte[] btRS = new byte[64];

byte[] btR = r.ToByteArray();

byte[] btS = s.ToByteArray();

Array.Copy(btR, btR.Length - 32, btRS, 0, 32);

Array.Copy(btS, btS.Length - 32, btRS, 32, 32);

return new BigInteger[] { r, s };

}

SM2算法是基于ECC算法的，签名同样返回2个大数，共64byte。由于原来RSA算法已很普遍支持，要实现RSA的签名验签都有标准库的实现，而SM2是国密算法在国际上还没有标准通用，算法Oid标识在X509标准中是没定义的。在.Net或Java中可以基于使用BouncyCastle加密库实现，开源的也比较好学习扩展。SM2算法验签可以使用软验签，即可以不需要使用硬件设备，同样使用原始数据、签名、证书(公钥)来实现对签名方验证，保证数据完整性未被篡改。验证过程同样需先摘要原文数据，公钥在证书中是以一个66byte的BitString，去掉前面标记位即64byte为共钥坐标(x,y)，中间分割截取再以Hex方式转成BigInteger大数计算，验签代码如下：

public static bool Verify(byte[] msg, byte[] signData, byte[] certData)

{

X509Certificate2 x5092 = new X509Certificate2(certData);

byte[] certPK = x5092.GetPublicKey();

certPK = SubByte(certPK, 1, 64);

byte[] certPKX = SubByte(certPK, certPK.Length - 32 - 32, 32);

byte[] certPKY = SubByte(certPK, certPK.Length - 32, 32);

System.String strcertPKX = ByteToHexStr(certPKX);

System.String strcertPKY = ByteToHexStr(certPKY);

BigInteger biX = new BigInteger(strcertPKX, 16);

BigInteger biY = new BigInteger(strcertPKY, 16);

ECFieldElement x = new FpFieldElement(ecc_p, biX);

ECFieldElement y = new FpFieldElement(ecc_p, biY);

ECPoint userKey = new FpPoint(ecc_curve, x, y);

SM3Digest sm3 = new SM3Digest();

byte[] z = Sm2GetZ(Encoding.Default.GetBytes(userId), userKey);

sm3.BlockUpdate(z, 0, z.Length);

byte[] p = msg;

sm3.BlockUpdate(p, 0, p.Length);

byte[] md = new byte[32];

sm3.DoFinal(md, 0);

byte[] btR = SubByte(signData, 0, 32);

byte[] btS = SubByte(signData, 32, 32);

System.String strR = ByteToHexStr(btR);

System.String strS = ByteToHexStr(btS);

BigInteger r = new BigInteger(strR, 16);

BigInteger s = new BigInteger(strS, 16);

// e_

BigInteger e = new BigInteger(1, md);

// t

BigInteger t = r.Add(s).Mod(ecc_n);

if (t.Equals(BigInteger.Zero))

return false;

// x1y1

ECPoint x1y1 = ecc_point_g.Multiply(s);

x1y1 = x1y1.Add(userKey.Multiply(t));

// R

BigInteger R = e.Add(x1y1.X.ToBigInteger()).Mod(ecc_n);

return r.Equals(R);

}

制作SM2证书

基于BouncyCastle开源库，可以轻松制作X509证书、CRL、pkcs10、pkcs12，支持国际通用的RSA、ECC算法。制作SM2证书可以通过扩展BouncyCastle库来实现，需加入SM2签名算法DerObjectIdentifier标识1.2.156.10197.1.501(基于SM3的SM2算法签名)，密钥对的生成使用国密推荐曲线参数，然后如上所示自行实现SM2签名验证算法。X509证书由证书主体、证书签名算法标识、签名组成，和RSA证书主要不同的是SM2证书的签名算法标识和签名，及证书公钥使用ECKeyParameters。生成自签名SM2证书代码如下：

SM2证书生成

public static Org.BouncyCastle.X509.X509Certificate MakeRootCert(string filePath, IDictionary subjectNames)

{

AsymmetricCipherKeyPair keypair = SM2CryptoServiceProvider.SM2KeyPairGenerator.GenerateKeyPair();

ECPublicKeyParameters pubKey = (ECPublicKeyParameters)keypair.Public; //CA公钥

ECPrivateKeyParameters priKey = (ECPrivateKeyParameters)keypair.Private; //CA私钥

X509Name issuerDN = new X509Name(GetDictionaryKeys(subjectNames), subjectNames);

X509Name subjectDN = issuerDN; //自签证书，两者一样

SM2X509V3CertificateGenerator sm2CertGen = new SM2X509V3CertificateGenerator();

//X509V3CertificateGenerator sm2CertGen = new X509V3CertificateGenerator();

sm2CertGen.SetSerialNumber(new BigInteger(128, new Random())); //128位

sm2CertGen.SetIssuerDN(issuerDN);

sm2CertGen.SetNotBefore(DateTime.UtcNow.AddDays(-1));

sm2CertGen.SetNotAfter(DateTime.UtcNow.AddDays(365 * 10));

sm2CertGen.SetSubjectDN(subjectDN);

sm2CertGen.SetPublicKey(pubKey); //公钥

sm2CertGen.SetSignatureAlgorithm("SM3WITHSM2");

sm2CertGen.AddExtension(X509Extensions.BasicConstraints, true, new BasicConstraints(true));

sm2CertGen.AddExtension(X509Extensions.SubjectKeyIdentifier, false, new SubjectKeyIdentifierStructure(pubKey));

sm2CertGen.AddExtension(X509Extensions.AuthorityKeyIdentifier, false, new AuthorityKeyIdentifierStructure(pubKey));

sm2CertGen.AddExtension(X509Extensions.KeyUsage, true, new KeyUsage(6));

Org.BouncyCastle.X509.X509Certificate sm2Cert = sm2CertGen.Generate(keypair);

sm2Cert.CheckValidity();

sm2Cert.Verify(pubKey);

return sm2Cert;

}

X509证书使用ASN1语法进行编码，是用类型标识、长度和值序列来描述数据结构的。SM2证书在制作设置公钥时，默认会带ECKeyParameters参数，并没有SM2的公钥参数1.2.156.10197.1.301，因此需要自己写个SM2椭圆曲线密码算法标识对象，这样在生成的证书中就可以看到公钥参数字段，如下所示：

SM2证书公钥标识

using System;

using Org.BouncyCastle.Asn1.X509;

using Org.BouncyCastle.Asn1;

namespace Common.Security

{

public class SM2AlgorithmIdentifier

: AlgorithmIdentifier

{

private readonly bool parametersDefined;

public SM2AlgorithmIdentifier(

DerObjectIdentifier objectID):base(objectID)