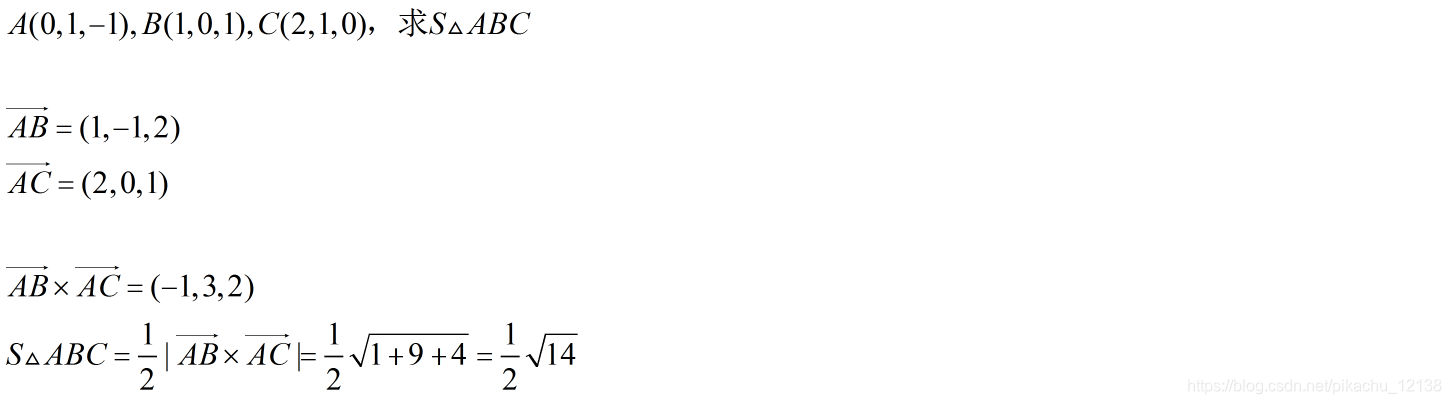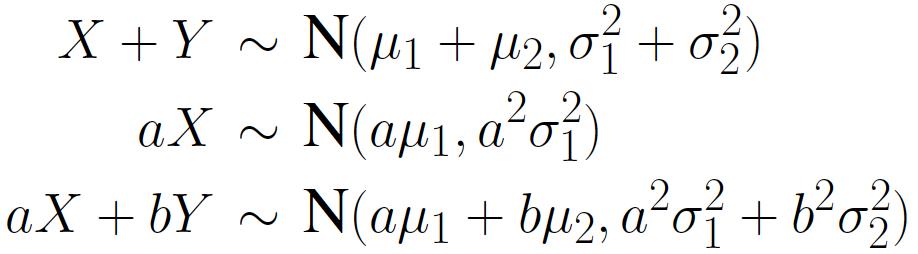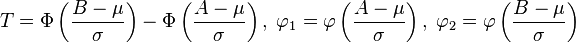两向量的向量积
两向量 a 与 b 的向量积(外积)是一个向量,记做 a × b \mathbf{a}\times \mathbf{b} a×b 或 [ a b ] [\mathbf{a}\mathbf{b}] [ab],它的模是
∣ a × b ∣ = ∣ a ∣ ∣ b ∣ sin ∠ ( a , b ) |\mathbf{a}\times \mathbf{b}| = |\mathbf{a}||\mathbf{b}|\sin\angle(\mathbf{a},\mathbf{b}) ∣a×b∣=∣a∣∣b∣sin∠(a,b)
它的方向与 a 和 b 都垂直,并且按 a, b, a × b \mathbf{a}\times\mathbf{b} a×b 这个顺序构成右手标架 { O ; a , b , a × b } \{O;\mathbf{a},\mathbf{b},\mathbf{a}\times\mathbf{b}\} {O;a,b,a×b}
-
两个不共线向量 a 与 b 的向量积的模,等于以 a 与 b 为边所构成的平行四边形的面积
-
两向量 a 与 b 共线的充分必要条件是 a × b = 0 \mathbf{a}\times\mathbf{b} = \mathbf{0} a×b=0
当 a 和 b 共线时, sin ∠ ( a , b ) = 0 \sin\angle(\mathbf{a},\mathbf{b}) = 0 sin∠(a,b)=0或者至少一个为零向量; 当 sin ∠ ( a , b ) = 0 \sin\angle(\mathbf{a},\mathbf{b}) = 0 sin∠(a,b)=0时或者其至少一个为零向量,a 和 b 共线 -
向量积是 反交换 的: a × b = − ( b × a ) \mathbf{a}\times\mathbf{b} = - (\mathbf{b}\times\mathbf{a}) a×b=−(b×a)
-
向量积满足关于数因子的结合律: λ ( a b ) = ( λ a ) × b = a × ( λ b ) \lambda(\mathbf{a}\mathbf{b}) = (\lambda\mathbf{a})\times\mathbf{b} = \mathbf{a}\times(\lambda\mathbf{b}) λ(ab)=(λa)×b=a×(λb)
-
向量积满足分配律: ( a + b ) × c = a × c + b × c (\mathbf{a}+\mathbf{b})\times\mathbf{c} = \mathbf{a}\times\mathbf{c}+\mathbf{b}\times\mathbf{c} (a+b)×c=a×c+b×c
c × ( a + b ) = a × c + b × c \mathbf{c}\times(\mathbf{a}+\mathbf{b}) = \mathbf{a}\times\mathbf{c}+\mathbf{b}\times\mathbf{c} c×(a+b)=a×c+b×c同样成立
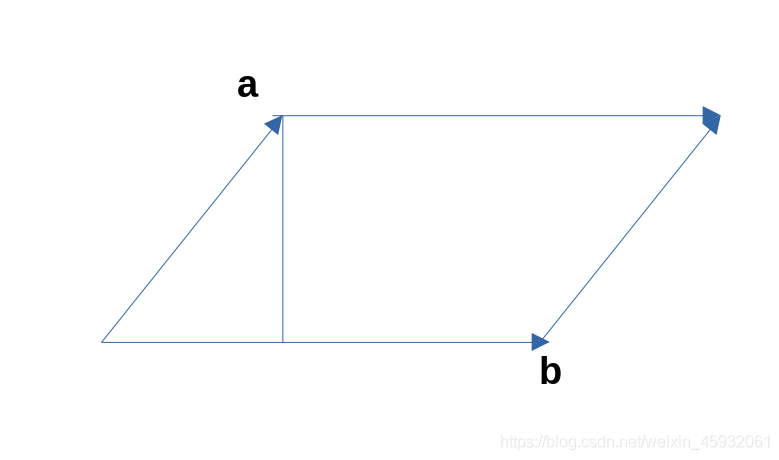
先证明 ( a + b ) × c 0 = a × c 0 + b × c 0 (\mathbf{a}+\mathbf{b})\times\mathbf{c}^{\mathbf{0}} = \mathbf{a}\times\mathbf{c}^{\mathbf{0}}+\mathbf{b}\times\mathbf{c}^{\mathbf{0}} (a+b)×c0=a×c0+b×c0
利用作图将 c 0 \mathbf{c}^{\mathbf{0}} c0, a, b, a × c 0 \mathbf{a}\times\mathbf{c}^{\mathbf{0}} a×c0, b × c 0 \mathbf{b}\times\mathbf{c}^{\mathbf{0}} b×c0, a + b \mathbf{a}+\mathbf{b} a+b, ( a + b ) × c 0 (\mathbf{a}+\mathbf{b})\times\mathbf{c}^{\mathbf{0}} (a+b)×c0的图像画出容易得出 ( a + b ) × c 0 = a × c 0 + b × c 0 (\mathbf{a}+\mathbf{b})\times\mathbf{c}^{\mathbf{0}} = \mathbf{a}\times\mathbf{c}^{\mathbf{0}}+\mathbf{b}\times\mathbf{c}^{\mathbf{0}} (a+b)×c0=a×c0+b×c0
再两边乘以 ∣ c ∣ |\mathbf{c}| ∣c∣即可得出 -
如果 a = X 1 i + Y 1 j + Z 1 k b = X 2 i + Y 2 j + Z 2 k \mathbf{a} = X_{1}\mathbf{i} + Y_{1}\mathbf{j}+Z_{1}\mathbf{k}\quad\mathbf{b} = X_{2}\mathbf{i} + Y_{2}\mathbf{j}+Z_{2}\mathbf{k} a=X1i+Y1j+Z1kb=X2i+Y2j+Z2k,那么
a × b = ∣ Y 1 Z 1 Y 2 Z 2 ∣ i + ∣ Z 1 X 1 Z 2 X 2 ∣ j + ∣ X 1 Y 1 X 2 Y 2 ∣ k \mathbf{a}\times\mathbf{b} = \left| \begin{array}{cc} Y_{1} & Z_{1} \\ Y_{2} & Z_{2} \end{array} \right|\mathbf{i} + \left| \begin{array}{cc} Z_{1} & X_{1} \\ Z_{2} & X_{2} \end{array} \right|\mathbf{j} + \left| \begin{array}{cc} X_{1} & Y_{1} \\ X_{2} & Y_{2} \end{array} \right|\mathbf{k} a×b=∣∣∣∣Y1Y2Z1Z2∣∣∣∣i+∣∣∣∣Z1Z2X1X2∣∣∣∣j+∣∣∣∣X1X2Y1Y2∣∣∣∣k
或则写成
a × b = ∣ i j k X 1 Y 1 Z 1 X 2 Y 2 Z 2 ∣ \mathbf{a}\times\mathbf{b} = \left| \begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ X_{1} & Y_{1}& Z_{1}\\ X_{2} & Y_{2}& Z_{2} \end{array} \right| a×b=∣∣∣∣∣∣iX1X2jY1Y2kZ1Z2∣∣∣∣∣∣