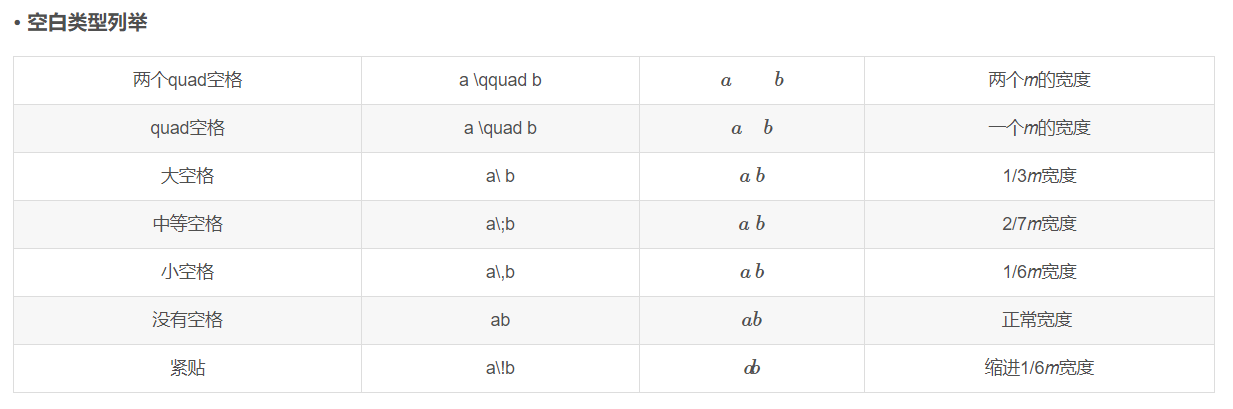
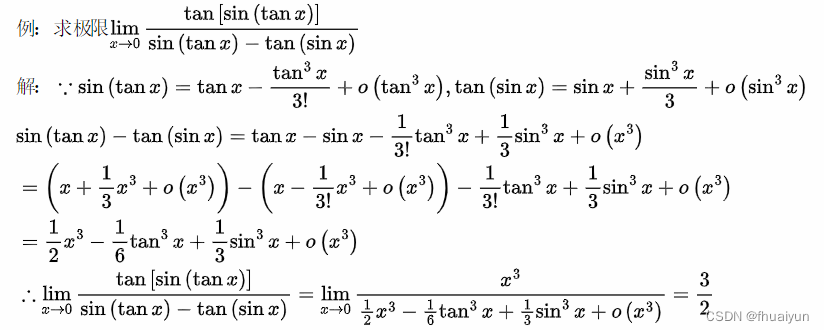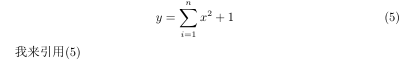有些复杂的极限题，里面会涵盖着各种各样的函数，这些群魔乱舞的函数加大了我们计算极限的难度，此时想：如果可以将这些函数统一成一样的形式该多好?此时，就有我们的泰勒公式了。

1.泰勒公式怎么用：

指数函数，三角函数，反三角函数，对数函数等函数，同时若干个在极限中出现时，使用泰勒公式将它们一致化，从而容易计算。我和另一位学长做的笔记例题如下：

本题利用泰勒公式，将多种类型的函数转化为统一的多项式函数，原极限进而转变为有理函数的极限，而这种函数极限是非常容易求的。这就是泰勒公式求极限的核心。
另外，对于泰勒展开而言，展开到几阶(精度为多少)也是非常关键的。本题的技巧总结提供了一个方法，更加详细的见下面内容。

2.精度如何确定(泰勒展开到几阶)：

泰勒展开有两大令人头疼的：1.这个函数的展开公式是啥？2.展开到第几项（精度为多少）？
针对第一点，直接背就行了，背不会可以自己求导推几遍。还记不住的可以看别人总结的记忆技巧，如下图是我和另一位学长做的知识点笔记，下图左边是一些常见的泰勒公式和一些记忆技巧：

同时，右边强调了精度的重要性，如果不了解精度盲目展开的话，非常容易出错，上面导图中即有错例。所以我们接下来看最关键和最有难度第二点：精度如何确定？

主要采用先整体后局部的方法：

1.确定整体精度：

极限 ${\lim }_{x\to x_0}\frac{A}{B}$ （其中$A，B$表示一个式子），首先确定谁更容易确定精度，如果$B$更容易确定精度，则$A$暂时不变，先判断$B$的精度，再根据B的精度来确定$A$的精度。
比如$B$直接为 $a{x}^m$ 或可以通过等价转变为 $a{x}^m$，那么直接可以确定B的精度为$m$，进而确定A的精度为$m$。
例： ${\lim }_{x\to x_0}\frac{A}{sin{x}^{2}ln(1+x)}={\lim }_{x\to x_0}\frac{A}{x^3}$ ，所以进而确定$A$的精度为3，需要完全展开到 $x_{}^3$

2.再确定局部：

上述通过更容易确定精度的$B$得出$A$的精度为$m$。因此，接下来需要对A进行展开，展开到 $x^m$ ，并且不漏项，这有一定的难度。针对这个，我总结了下面3个技巧：
1.若A为"$函数f-函数g$"型：
比较简单，直接通过泰勒公式将函数f和函数g展开到所需精度即可（若某一个函数为多项式函数，则不用考虑展开）。如图1中题1.1所示：分子确定精度为4，需要展开到 $x^4$ 。因此将 $\sqrt{1+x^2}$ 展开至$x^4$，$p.s.$前面是多项式函数，不用管。
2.若A含有"$函数f\times 函数g$"型：
有公式：左低+右高=精度；左高+右低=精度。
左低代表为左边函数展开最低项为 x 的多少次方（不考虑系数），右高代表为右边函数展开最高项为 $x$ 的多少次方（不考虑系数），以此类推。根据公式，我们可以先展开左边函数和右边函数的第一项，得左低和右低，再根据公式，得到左边函数和右边函数应展开到x的多少次方（左高和右高），具体操作如下：
以图2右侧的易错点为例：展开 $ln(1+x)ln(1-x)$ ，由于左边函数 $ln(1+x)$ 和右边函数 $ln(1-x)$ 展开的第一项都为 $x$ （不考虑系数），所以左低和右低为1，根据公式，左高和右高都为3。因此 $ln(1+x)$ 和 $ln(1-x)$ 都要展开到含 $x^3$ ，即有正确解法。
3.若A含有"复合函数展开"型：
有公式：内低×外高=精度；内高×外低=精度。
内低表示内层函数展开最低为$x$ 的多少次方（不考虑系数），外高代表为外层函数展开最高项为 $x$ 的多少次方（不考虑系数），以此类推。根据公式，我们可以先展开内层函数和外层函数的第一项，得内低和外低，再根据公式，得到内层函数和外层函数应展开到x的多少次方（内高和外高），具体操作如下：
例：将 $ln(1+sinx)$ 展开到精度为4。外层函数 $ln(1+x)$ 最低为$x$的一次方，根据公式，内高为4，即 $sinx$ 展开到 $x$ 的四次方。故有： $x\to 0，sinx\sim x-\frac{x^3}{3!}+0\cdot \frac{x^4}{4!}$ ，同时反过来，内层函数最低也为x的一次方，根据公式，外层函数也需要展开到 $x$ 的四次方。有： $x\to 0，ln(1+x)\sim x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}$ ，此时带入复合，并将高于4次方的去除即有： $x\to 0，ln(1+sinx)\sim x-\frac{x^2}{2}+\frac{x^3}{6}-\frac{x^4}{4}$ 。
这或许还不足以发挥公式的威力，试着用公式解决下面这道难题。

到此为止！
我是煜神学长，考研我们一起加油！！！

关注GZH：鱼跃考研，了解考研数学提分利器思维导图