题目

实现SM2椭圆曲线公钥密码算法，对给出的英文消息进行加密得到密文，并能通过密文解密出明文。

环境

Windows10，MinGW-W64-builds-4.3.5，miracl 7.0.1

方案设计

背景

SM2椭圆曲线公钥密码算法，SM3密码杂凑算法

原理

椭圆曲线公钥密码所基于的曲线性质如下：
──有限域上椭圆曲线在点加运算下构成有限交换群，且其阶与基域规模相近；
──类似于有限域乘法群中的乘幂运算，椭圆曲线多倍点运算构成一个单向函数。
解密的正确性：
因为PB=dBG，C1=kG=(x1,y1),由解密算法的第三步可得dBC1=dBkG=k(dBG)=kPB=(x2,y2)，所以解密算法第四步得到的t与加密算法第五步得到的t相等，由C2⊕t，便得到明文M。

算法步骤

加密算法
设需要发送的消息为比特串?， klen 为?的比特长度。为了对明文?进行加密，作为加密者的用户A应实现以下运算步骤：
A1：用随机数发生器产生随机数? ∈ [?,?−?]；
A2：计算椭圆曲线点??=[?]? = (??,??)，将??的数据类型转换为比特串；
A3：计算椭圆曲线点? = [?]??，若?是无穷远点，则报错并退出；
A4：计算椭圆曲线点[?]??=(??,??)，将坐标??,??的数据类型转换为比特串；
A5：计算? = ???(??||??,????)，若?为全0比特串，则返回A1；
A6：计算?? = ?⊕?;
A7：计算?? = ????(??||?||??);
A8：输出密文? = ??||??||??。
解密算法
设klen为密文中??的比特长度。为了对密文? = ??||??||??进行解密，作为解密者的用户B应实现以下运算步骤：
B1：从?中取出比特串??，将??的数据类型转换为椭圆曲线上的点，验证??是否满足椭圆曲线方程，若不满足则报错并退出;
B2：计算椭圆曲线点?=[?]??，若?是无穷远点，则报错并退出;
B3：计算[??]??=(??,??)，将坐标??,??的数据类型转换为比特串;
B4：计算? = ???(??||??,????)，若?为全0比特串，则报错并退出;
B5：从?中取出比特串??，计算?’= ??⊕?;
B6：计算? = ????(?? ||?’||??)，从?中取出比特串??，若? ≠ ??，则报错并退出;
B7：输出明文 M’。

方案实现

流程图

加密

解密

主要函数

epoint* epoint_init();初始化一个点
void ecurve_init(A,B,p,type);初始化椭圆曲线 y2 =x3 + Ax + B mod p
BOOL epoint_set(x,y,lsb,p);设置点p的（x,y）坐标，（x,y）在曲线上则返回true
void ecurve_mult(k,p,pa);倍点运算
int epoint_get(p,x,y);取出p点的x,y坐标
int big_to_bytes(max,x,ptr,justify);将大数转换成比特串
void bytes_to_big(len,ptr,x); 将比特串转换成大数
BOOL point_at_infinity§;判断p点是否无穷远点

C代码

/*********************************************************** 推荐使用素数域256位椭圆曲线。 * 椭圆曲线方程：y2 = x3 + ax + b。*********************************************************/
#include <stdio.h>
#include <miracl.h>
#include <time.h>
#include <string.h> 
#define MSG_MAX 1000
#define N  3
#define NUM_W  132mr_small GG(int j, mr_small x, mr_small y, mr_small z);
mr_small FF(int j, mr_small x, mr_small y, mr_small z);
void BtoW(int i, mr_small b[][16], mr_small *W);
void CF(int i, mr_small V[][8], mr_small *W);
mr_small move(mr_small x, int n);
mr_small P0(mr_small x);
mr_small P1(mr_small x);
mr_small Tj(int j);
int hex2d(char a, char b);
void sm3(int mlen, unsigned char *msg,unsigned char *hash);
void str2hex(char *str, char *hex);
void hex2str(char *hex, char *str);
int KDF(unsigned char x2y2[], unsigned int klen, unsigned char t[]);int main(void)
{miracl *mip = mirsys(1000,16);mip->IOBASE = 16; FILE    *fp;big     p, a, b, n, Gx, Gy,     x, y, k, v, dB, h;epoint  *G, *S, *PB, *C1, *C2;unsigned int    klen;unsigned char    hex[MSG_MAX], msg[MSG_MAX]="encryption standard";unsigned char    crp[MSG_MAX+96], tmp[MSG_MAX+64], t[MSG_MAX];char ch;int     i=0;fp = fopen("9.txt", "r");printf("msg :");while((ch = fgetc(fp)) != EOF){msg[i++] = ch;putchar(ch);} msg[i]='\0'; puts("\n");p = mirvar(0); a = mirvar(0); b = mirvar(0); n = mirvar(0); Gx = mirvar(0); Gy = mirvar(0); k = mirvar(0); v = mirvar(0); dB = mirvar(0); x = mirvar(0); y = mirvar(0); h = mirvar(1);str2hex(msg, hex);  cinstr(v, hex); klen = big_to_bytes(0, v, msg, FALSE);fp = fopen("parameter2.txt", "r");cinnum(p, fp); cinnum(a, fp); cinnum(b, fp);cinnum(n, fp); cinnum(Gx, fp); cinnum(Gy, fp);fclose(fp);printf("p= ");cotnum(p, stdout); printf("a= ");cotnum(a, stdout); printf("b= ");cotnum(b, stdout); printf("n= ");cotnum(n, stdout); printf("x= ");cotnum(Gx, stdout); printf("y= ");cotnum(Gy, stdout);putchar('\n');G = epoint_init(); S = epoint_init(); PB = epoint_init();C1 = epoint_init(); C2 = epoint_init();ecurve_init(a, b, p, MR_PROJECTIVE); epoint_set(Gx, Gy, 0, G);char *str="1649AB77A00637BD5E2EFE283FBF353534AA7F7CB89463F208DDBC2920BB0DA0";printf("dB= ");instr(dB, str);cotnum(dB, stdout);ecurve_mult(dB, G, PB);// str="4C62EEFD6ECFC2B95B92FD6C3D9575148AFA17425546D49018E5388D49DD7B4F";//// printf("k = ");instr(k, str);cotnum(k, stdout);
//encryptionwhile(1){irand(time(NULL)); decr(n, 2, v); bigrand(v, k); incr(k, 1, k);//cotnum(k, stdout);ecurve_mult(k, G, C1); epoint_get(C1, x, y);big_to_bytes(0 , x, crp, FALSE); big_to_bytes(0 , y, crp+32, FALSE);ecurve_mult(h, G, S); if(point_at_infinity(S)){ printf("S at infinity\n");return -1;}ecurve_mult(k, PB, C2); epoint_get(C2, x, y);big_to_bytes(0 , x, tmp, FALSE); big_to_bytes(0 , y, tmp+32,FALSE);if(KDF(tmp, klen, t))break;}// printf("\nt =");for (i=0;i<klen;i++) {crp[i+64] = msg[i] ^ t[i];// printf("%c",t[i]);} putchar('\n');big_to_bytes(0, x, tmp, FALSE); memcpy(tmp+32, msg, klen);big_to_bytes(0, y, tmp+32+klen, FALSE); sm3(64+klen, tmp, crp+64+klen);printf("\nciphertext:\n");for(i = 0; i < 64+32+klen; i++){printf("%02x",crp[i]);}putchar('\n');//decryptionbytes_to_big(32,crp,x); bytes_to_big(32,crp+32,y);ecurve_init(a, b, p, MR_PROJECTIVE);if(!epoint_set(x, y, 0, C1)){ printf("C1 not on curve\n");return -1;}ecurve_mult(h, C1, S); if(point_at_infinity(S)){ printf("S at infinity\n");return -1;}ecurve_mult(dB, C1, C2); epoint_get(C2, x, y);big_to_bytes(0, x, tmp, FALSE); big_to_bytes(0, y, tmp+32, FALSE);if(!KDF(tmp, klen, t)) {printf("t is 0\n");return -1;}// printf("\nt'=");for(i = 0; i < klen; i++){msg[i] = crp[i+64] ^ t[i];// printf("%02x",t[i]);}putchar('\n');big_to_bytes(0, x, tmp, FALSE); memcpy(tmp+32, msg, klen);big_to_bytes(0, y, tmp+32+klen, FALSE); sm3(64+klen, tmp, t);if(strcmp(t, crp+64+klen)){printf("u != C3\n");return -1;}else {printf("\nrecover message correctly.\n");}bytes_to_big(klen, msg, v); otstr(v, tmp); hex2str(tmp, t);printf("\nmsg':%s\n",t);return 0;
}int KDF(unsigned char x2y2[], unsigned int klen, unsigned char t[])
{unsigned int ct = 1;unsigned char buf[68] = {0}, *p=t, tmp[MSG_MAX];int i, n;n = klen%32;memcpy(buf, x2y2, 64);for (i=0; i < klen/32; i++) {buf[64] = (ct >> 24) & 0xff;buf[65] = (ct >> 16) & 0xff;buf[66] = (ct >> 8 ) & 0xff;buf[67] =  ct        & 0xff;sm3(68, buf, p);p+=32;ct++;}if (n) {buf[64] = (ct >> 24) & 0xff;buf[65] = (ct >> 16) & 0xff;buf[66] = (ct >> 8 ) & 0xff;buf[67] =  ct        & 0xff;sm3(68, buf, tmp);}memcpy(p, tmp, n);t[klen] = '\0';for (i=0; i < klen; i++) {if (t[i]) {break;}}if(i < klen)return 1;elsereturn 0;// t is 0}void sm3(int mlen, unsigned char *msg, unsigned char *hash)
{miracl *mip = mirsys(1000,16);mip->IOBASE = 16;int     i, j, n; unsigned long long     len;mr_small W[NUM_W]={0}, b[N][16]={0}, v[N+1][8], *p;unsigned char *ph=hash;big     m;v[0][0] = 0x7380166f; v[0][1] = 0x4914b2b9; v[0][2] = 0x172442d7; v[0][3] = 0xda8a0600;v[0][4] = 0xa96f30bc; v[0][5] = 0x163138aa; v[0][6] = 0xe38dee4d; v[0][7] = 0xb0fb0e4e;m = mirvar(0);bytes_to_big(mlen, msg, m);// printf("m = ");cotnum(m, stdout);len = numdig(m)*4; sftbit(m, 1, m);incr(m, 1, m);if (len % 512 < 448){n = len/512 + 1;                                           sftbit(m, 511-(len%512), m);             }else {n = len/512 + 2;  sftbit(m, 1023-(len%512), m);}                  incr(m, len, m);p = m->w;for (i = n-1; i >=0; i--){for (j = 15; j >= 0; j--){b[i][j] = *p++;}  }for (i = 0; i < n; i++) {BtoW(i, b, W);  // 将消息分组??扩展生成132个字CF(i, v, W);    // 迭代压缩}for (j = 0; j < 8; j++) {sprintf(ph,"%08x", v[n][j]);ph+=8;}*ph='\0';mirkill(m);
}void str2hex(char *str, char *hex)
{char *p = hex;int i;for(i=0;str[i];i++){sprintf(p, "%02x",str[i]);p+=2;}*p='\0';// puts(hex);
}
void hex2str(char *hex, char *str)
{char *p = str,c;int i;for(i=0;hex[i];i+=2){c=hex2d(hex[i],hex[i+1]);*p++=c;}*p='\0';// puts(str);
}
int hex2d(char a, char b)
{//convert hex to 10int s=0;if('a'<=a && a<='f'){s+=(a-87)*16;}else if('A'<=a && a<='F'){s+=(a-55)*16;}else{s+=(a-48)*16;}if('a'<=b && b<='f'){s+=(b-87);}else if('A'<=b && b<='F'){s+=(b-55);}else{s+=(b-48);}return s;
}
void BtoW(int i, mr_small b[][16], mr_small *W)
{int j;for (j = 0; j < 16; j++) {W[j] = b[i][j];}for (j = 16; j < 68; j++) {W[j] = P1(W[j-16]^W[j-9]^move(W[j-3], 15))^move(W[j-13], 7)^W[j-6];}for (j = 0; j < 64; j++) {W[j+68] = W[j]^W[j+4];}
}
void CF(int i, mr_small V[][8], mr_small *W)
{mr_small R[8], ST[4];int j; int t;    for (j = 0; j < 8; j++) {R[j] = V[i][j];}for (j = 0; j < 64; j++) { ST[0] = move(move(R[0], 12)+R[4]+move(Tj(j), j), 7);ST[1] = ST[0] ^ move(R[0], 12); ST[2] = FF(j, R[0], R[1], R[2]) + R[3] + ST[1] + W[j+68];ST[3] = GG(j, R[4], R[5], R[6]) + R[7] + ST[0] + W[j];R[3] = R[2];                    R[2] = move(R[1], 9);R[1] = R[0];R[0] = ST[2];R[7] = R[6];R[6] = move(R[5], 19);R[5] = R[4];R[4] = P0(ST[3]);   }for (j = 0; j < 8; j++) {V[i+1][j] = V[i][j] ^ R[j];}}mr_small FF(int j, mr_small x, mr_small y, mr_small z)
{if (j < 16 && j >= 0) {return x^y^z;} if(j >=16 && j < 64) {return (x&y)|(x&z)|(y&z);}return -1;
}
mr_small GG(int j, mr_small x, mr_small y, mr_small z)
{if (j < 16 && j >= 0) {return x^y^z;} if(j >=16 && j < 64) {return (x&y)|(~x&z);}return -1;
}
mr_small move(mr_small x, int n)
{mr_small y , z;                               y = x << n;z = x >> (sizeof(x)*8-n);z = y | z;return z;
}
mr_small P0(mr_small x)
{return x^move(x, 9)^move(x, 17);
}
mr_small P1(mr_small x)
{return x^move(x, 15)^move(x, 23);
}
mr_small Tj(int j)
{if (j >=0 && j <16){return 0x79cc4519;}if (j >=16 && j <64){return 0x7a879d8a;}return -1;
}

测试

数据

FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0

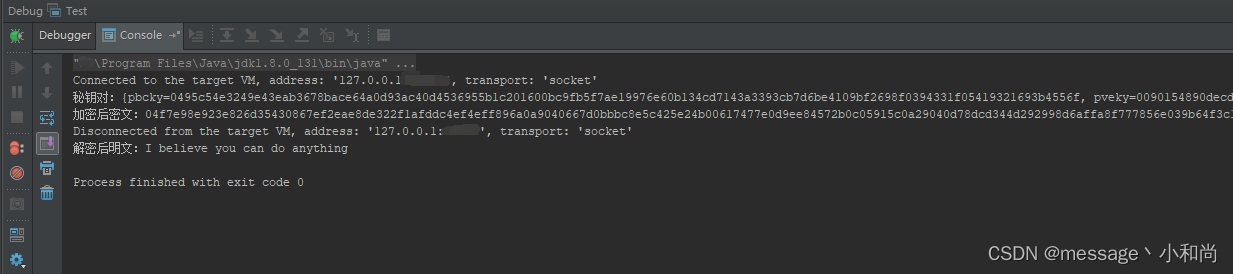
结果

注意问题

对于连接运算可以利用big_to_bytes函数把大数直接转换成比特串存入字符型数组，一个unsigned char有8比特，256位长的数可以用unsigned char s[32]来存储，连接的时候只需要依次存入数组。然后根据算法调用相应的函数对数组进行操作即可。用bytes_to_big函数可以把比特串还原成大数。