导论
SM2是国家密码管理局于2010年12月17日发布的椭圆曲线公钥密码算法,在我们国家商用密码体系中被用来替换RSA算法。
国产SM2算法,是基于ECC的,但二者在签名验签、加密解密过程中或许有些许区别,目前鄙人还不太清楚,后期有机会的话会回来补充。
普通的软密钥,在签名验签、加密解密时,使用的0009规范;
如果是硬密钥,例如密码钥匙是0016规范(SKF),密码设备是0018规范(SDF);
在涉及一方签,另一方验时,需注意规范问题!!!
SM2基于椭圆曲线,公钥是曲线上的一点(x,y),即公钥由x和y分量组成。
ps:1024位的RSA算法,已经不安全了。
涉及标准文件
《GM_T 0003.1-2012SM2 椭圆曲线公钥密码算法第1部分:总则》
《GM_T 0003.2-2012SM2 椭圆曲线公钥密码算法第2部分:数字签名算法》
《GM_T 0003.3-2012SM2 椭圆曲线公钥密码算法第3部分:密钥交换协议》
《GM_T 0003.4-2012SM2 椭圆曲线公钥密码算法第4部分:公钥加密算法》
《GM_T 0003.5-2012SM2 椭圆曲线公钥密码算法第5部分:参数定义》
《GMT 0009-SM2 密码算法使用规范-报批稿》
《GMT 0016-智能密码钥匙密码应用接口规范》
《GMT 0018-密码设备应用接口规范》
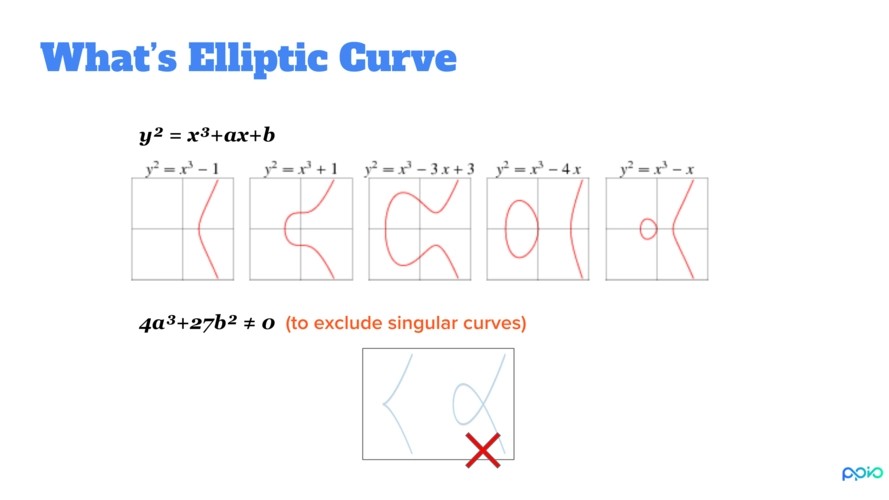
ECC椭圆曲线
BC库实现了一种C1||C2||C3的ECC加密方式,密文格式:C1||C2||C3,C1是带有04的公钥格式
对于这种,明确一下每一段的长度就很有必要了:
- C1: 公钥长度65字节,格式:04||x||y
- C3: hash长度32字节
- C2: 密文长度与明文长度一致
SM2
推荐的椭圆曲线、参数
椭圆曲线方程:y2 = x3 + ax + b
p= FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFF
a= FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFC
b= 28E9FA9E 9D9F5E34 4D5A9E4B CF6509A7 F39789F5 15AB8F92 DDBCBD41 4D940E93
n= FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF 7203DF6B 21C6052B 53BBF409 39D54123
Gx= 32C4AE2C 1F198119 5F990446 6A39C994 8FE30BBF F2660BE1 715A4589 334C74C7
Gy= BC3736A2 F4F6779C 59BDCEE3 6B692153 D0A9877C C62A4740 02DF32E5 2139F0A0
加密解密
参照SM2算法的第4部分:《GM_T 0003.4-2012SM2 椭圆曲线公钥密码算法第4部分:公钥加密算法》
涉及:《GM-T 0009》 9.2、9.3、7.2、7.4部分
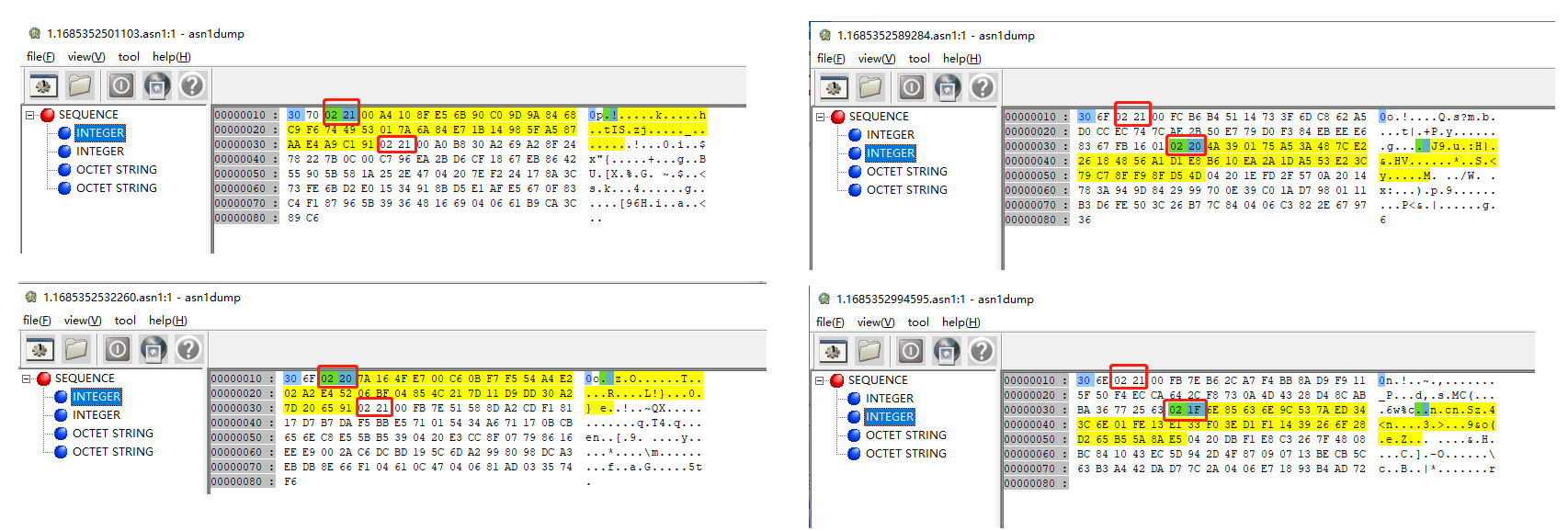
截取了几份同一公钥加密的结果,发现x/y分量不一定是正好32字节(0x20),可能多一个补位,或者少一位。
补位原因:以x分量值举例,因为x的第一字节值大于128(0x80),所以需要在前面加上0x00。
如果有朋友要把asn1编码的加密值转为C1C3C2时,注意一下补位问题哈。
签名验签
SM2签名
涉及:《GM-T 0009》 9.4、9.5、7.3部分
按照国密的规范,SM2签名结果r||s长度应该是(r:32字节)+(s:32字节)64字节,就算加个04头字节,也是65个字节。
r:随机数
s:签名值
但是,我参考网上有限的资料发现sign1签名MEQCIC24h6tnaKcOnxNZe93rtLFrKEqM9R3yG8/Ba2+tyE+3AiBTG46yfxJziYDlaH1WZjrCfRloIuMnfx5oyEVuwgbV0A==长度为96字节,这一看就是base64加密数据,源签名长度96/4*3=72字节。
SM2签名结果长度为64字节,为什么出来的是72字节?我咨询过好几个过35114的博客主,回复都是,我们是硬加密。/(ㄒoㄒ)/~~
其实,SM2签名结果数据是要经过asn.1(der格式)编码的,编码结果长度在70-72变化。
ASN1将签名产生的 r 和 s 看作两个整数,若其第一个字节最高位为 1,则在整数前插入0x00。
ECC签名
密钥长度:
公钥0x41(65字节) 私钥0x20(32字节)
签名格式:TLV嵌套格式。
签名的主体分为R和S两部分。R(或S)的长度等于ECC私钥长度。R(或S)前的T为0x02,签名T为0x30。总体格式如下:
30 + LEN1 + 02 + LEN2 + 00 (optional) + r + 02 + LEN3 + 00(optional) + s
*当r或s的第1字节大于0x80时,需要在r或s前加1字节0x00。
LEN3为,0x00(optional) + s 的字节长度。
LEN2为,0x00(optional) + r 的字节长度。
LEN1为,LEN2+LEN3+4字节长度。

参考链接:https://blog.csdn.net/m0_71405746/article/details/128253831
ASN1编码后,格式如下:
00 30 44 02 20 … 02 20 …
附:一个经三未加密机ECC签名的印章结构,详看签名值,硬件签名签名值可能不够64字节,为凑长度首为补0,此时我们系统的软验签就过不了。解决方式:如果首位是0,就让硬件再签一次吧。
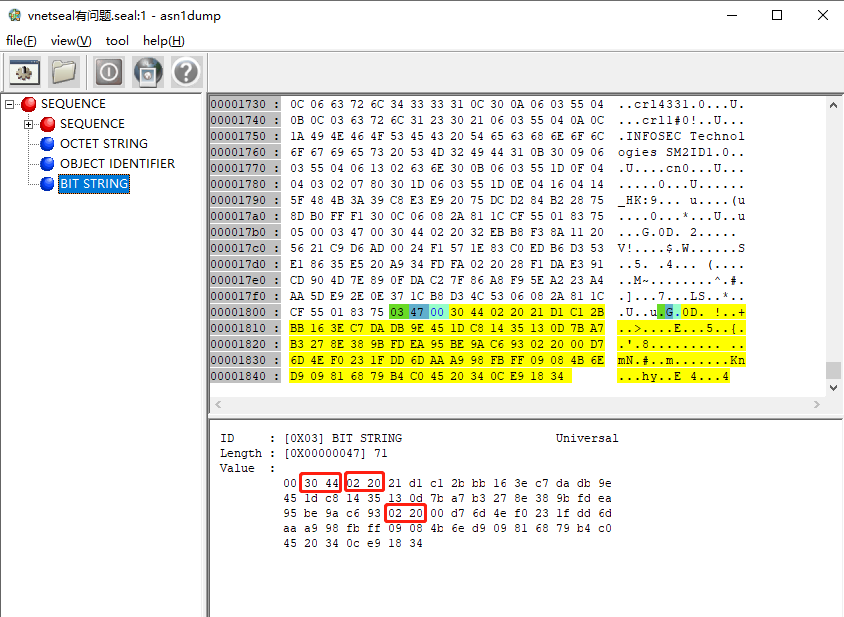
其中:
第1字节:若第一个字节最高位为 1,则在整数前插入0x00(有待验证)
第2字节:0x30表示一种通用的格式
第3字节:0x44表示后面跟了68个字节的数据
第4字节:0x02表示后面是一个整数
第5字节:0x20表示整数长度是32个字节
第38字节:0x02表示后面是个整数
第39字节:0x20表示整数长度是32个字节
第40字节:0x00表示签名值不足32位,首位补0了。
第40字节的0x00,即s的首位,就是软验证不过的问题所在吧。
SM2和ECC的区别
SM2基于ECC,却又不完全一样,有博主称:SM2与ecc的区别主要在于曲线参数的选择不同,另外在签名,验签的过程中也有一点区别,SM2的官方文档以及官方推荐参数可以参考
http://www.oscca.gov.cn/News/201012/News_1197.htm 。
《GM-T 0009》规范
相当于是《GM-T 0003》的补充用法。

密钥数据格式
私钥256位,公钥x/y分量各256位
注意:公钥内容为 04 || X || Y
公钥分量:x和y理论上是需要256位,即32字节。但实际上,也许是具体实现的误差,导致生成的公钥x、y分量不足32字节,发生补位情况,也会有33字节的情况。
公钥:理论是64字节(只含xy分量),也有可能是65字节(多个04、或者x多一字节、或y多一字节)

加解密

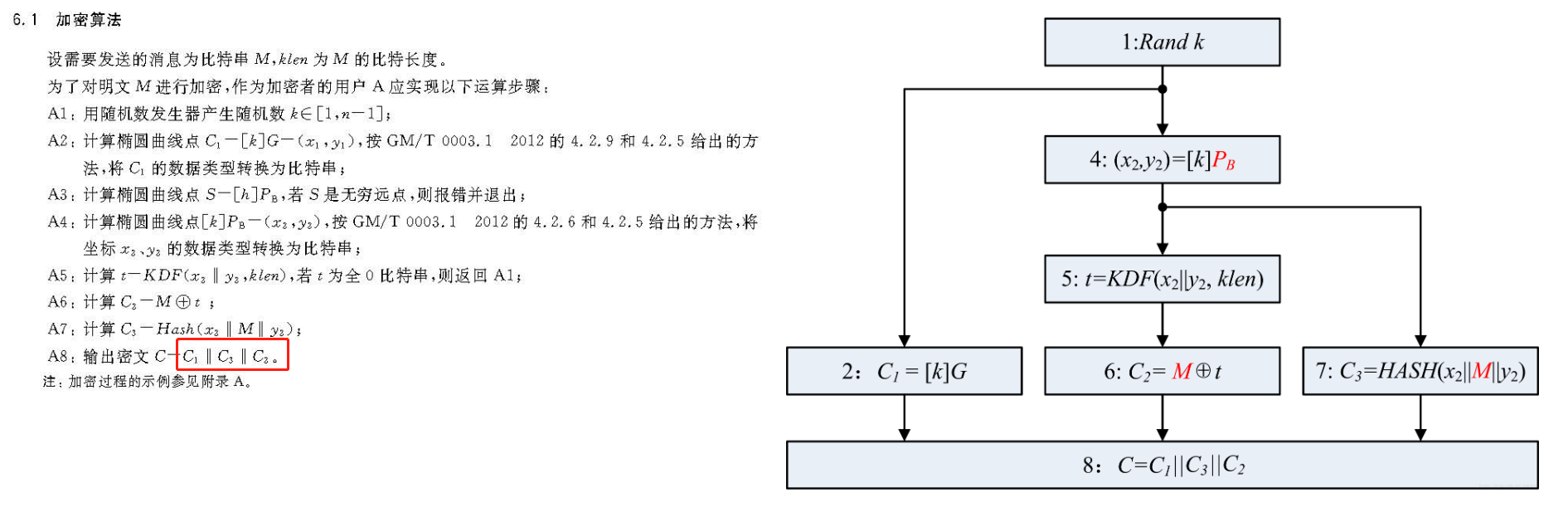
《GM-T 0009》 7.2部分的定义:加密数据格式
该规范要求输出的密文符合asn1标准,其中:
c1: x/y分量
c3: hash
c2:cipherText
c1/c2/c3这种叫法是《GMT 0003.4》定义的

注意:这里的xy分量是Integer类型,据说在ASN1编码规范中,对于Integer类型的数,有一个规则:如果数字的最高位是1,则需要再前面补充一个全0的八位组。

《GM-T 0009》 7.4部分的定义:密钥对保护数据格式(数字信封?)

签名验签

《GM-T 0009》 7.3部分的定义:签名数据格式

《GMT 0003.4》
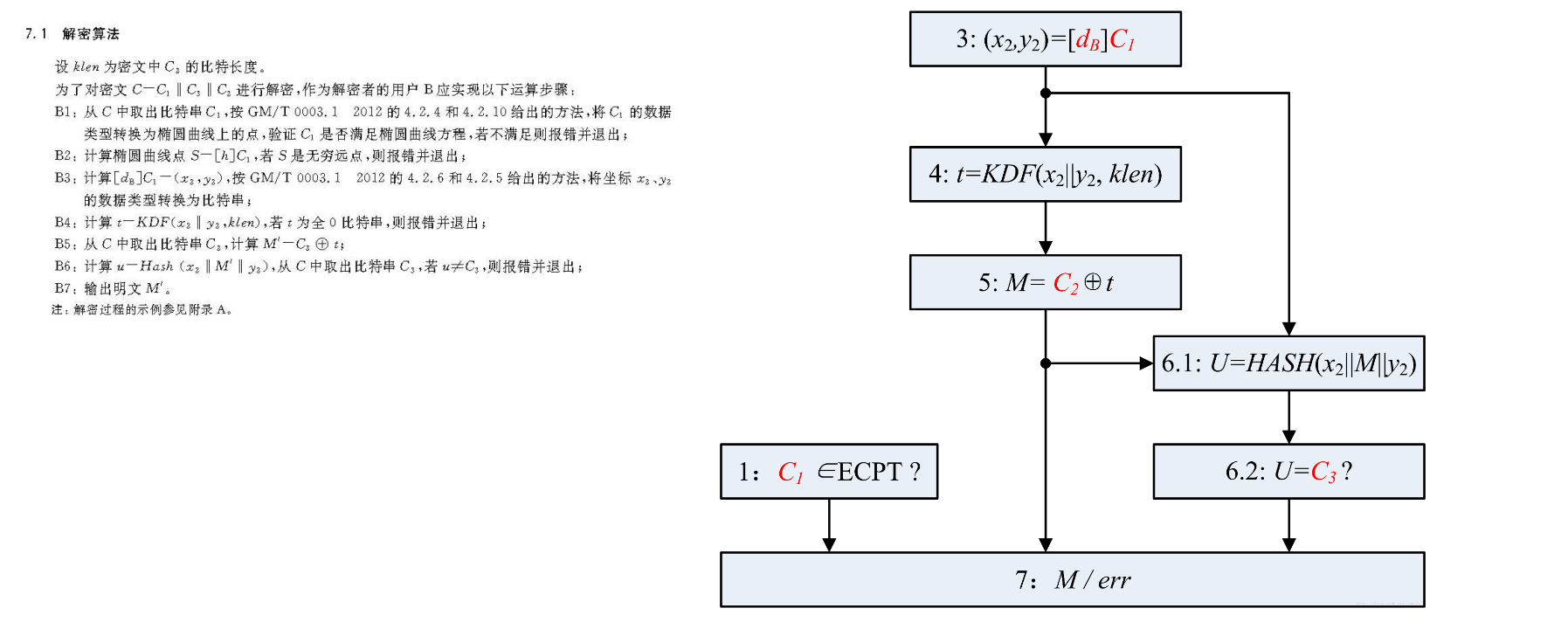
加解密


小剧场
java世界里,如何判断一个字节最高位是否是1?
十进制:128
二进制:1000 0000
十六进制:0x80
由于1000 0000值的特殊性,除了最高位是1,其余位全是0,任何值与其做【与】操作,低位都会被抵消为0。
举例:( x & 0x80)
- 结果等于0x80,则表示x最高位为1,即大于等于128;
- 不等于0x80,则x最高位为0,即小于128;