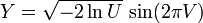泰勒公式记忆方法

$$\begin{gathered} \text{几个常见函数的泰勒公式} \\ f\left(x\right)=f\left(x_0\right)+f\prime \left(x_0\right)\left(x-x\right)+\frac{f^{{}^{\prime \prime }}\left(x_0\right)}{2!}{\left(x-x_0\right)}^2+\cdots +\frac{f^{\left(n\right)}\left(x_0\right)}{n!}{\left(x-x_0\right)}^n+R_n\left(x\right) \\ f\left(x\right)=f\left(0\right)+f\prime \left(0\right)x+\frac{f^{{}^{\prime \prime }}\left(0\right)}{2!}{x}^2+\cdots +\frac{f^{\left(n\right)}\left(0\right)}{n!}{x}^n+o\left(x^n\right) \\ {\mathrm{e}}^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+o\left(x^4\right)=\sum _{k=0}^n\frac{x^k}{k!}+o\left(x^n\right) \end{gathered}$$

$$\{\begin{array}{l}1.\text{写泰勒公式时，一些帮助记忆的方法：}\\ \left(1\right)\text{因为}\sin x,\cos x,\mathrm{a}\mathrm{r}\mathrm{c}\tan x,\frac{1}{1+x},\frac{1}{1+x^2}\text{求导会出现负号，所以这些函数展开会正负交替};\\ \left(2\right)\text{而}\tan x,\frac{1}{1-x}\text{求导符号保持不变，所以不会正负交替};\\ \left(3\right)\text{记住规律记不得第一项时，可以根据定义写出第一项，比如}\cos x\text{展开的第一项为}{\cos }^{\left(0\right)}0=1\\ \left(4\right)\mathrm{a}\mathrm{r}\mathrm{c}\sin x\text{的}\frac{A}{B}\frac{x^C}{C}\text{中，}A⟶B⟶C\text{分别加}1\text{，前面双阶乘，}C\text{无阶乘}\\ 2.{\text{具体使用时展开到几阶的原则：}}^{\prime \prime }{\text{分式同阶，相减互异}}^{\prime \prime }\end{array}$$