简介

AQS的全称为（AbstractQueuedSynchronizer），这个类在java.util.concurrent.locks包下面。

AQS是一个用来构建锁和同步器的框架，使用AQS能简单且高效地构造出应用广泛的大量的同步器，比如ReentrantLock，Semaphore，其他的诸如ReentrantReadWriteLock，SynchronousQueue，FutureTask等等皆是基于AQS的。当然，我们自己也能利用AQS非常轻松容易地构造出符合我们自己需求的同步器。

AQS原理分析

AQS原理概览

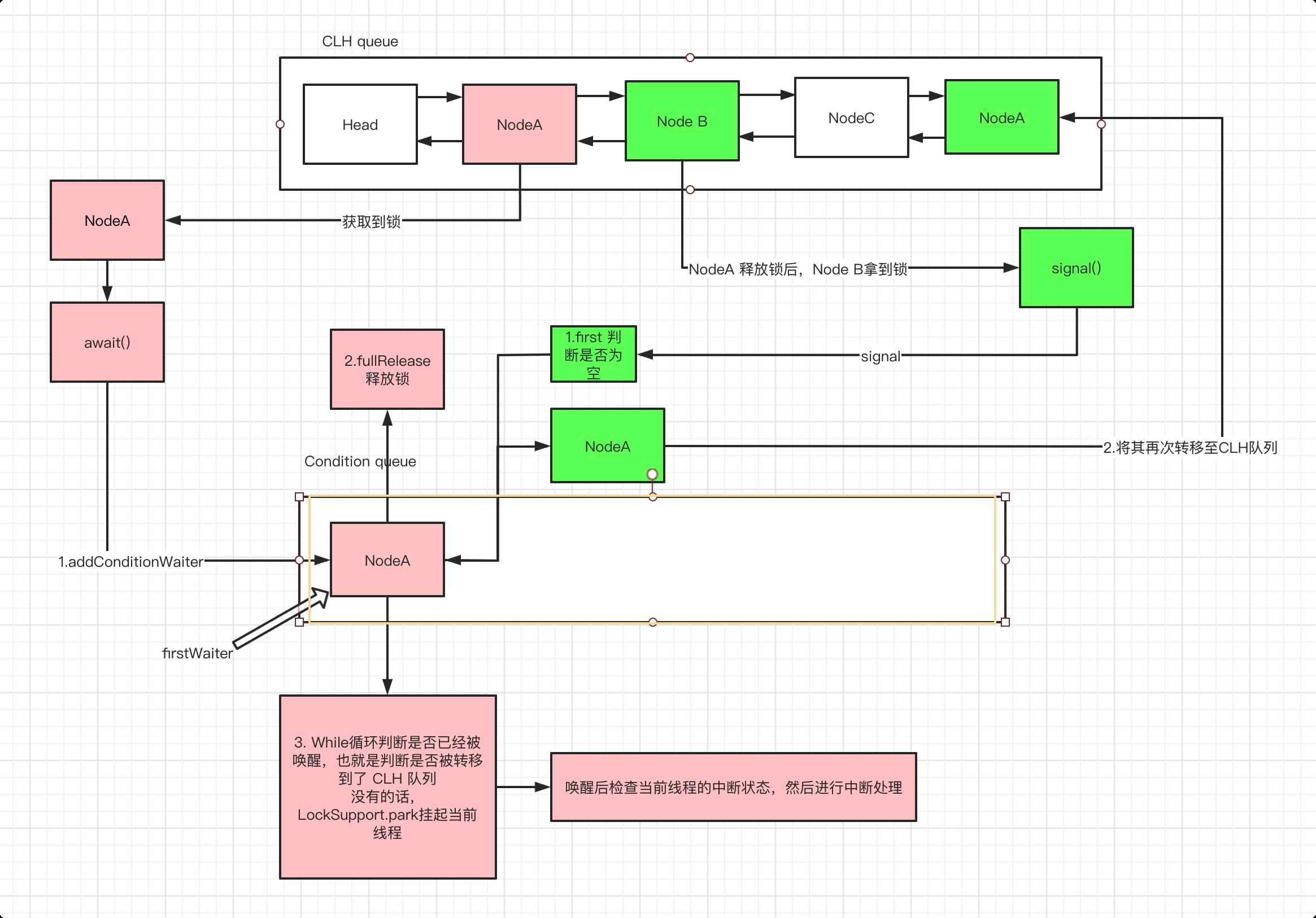
AQS核心思想是：如果被请求的共享资源空闲，则将当前请求资源的线程设置为有效的工作线程，并且将共享资源设置为锁定状态。如果被请求的共享资源被占用，那么就需要一套线程阻塞等待以及被唤醒时锁分配的机制，这个机制AQS是用CLH队列锁实现的，即将暂时获取不到锁的线程加入到队列中。

CLH(Craig,Landin,and Hagersten)队列是一个虚拟的双向队列（虚拟的双向队列即不存在队列实例，仅存在结点之间的关联关系）。
AQS是将每条请求共享资源的线程封装成一个CLH锁队列的一个结点（Node）来实现锁的分配。

AQS(AbstractQueuedSynchronizer)原理图：

AQS使用一个int成员变量来表示同步状态，通过内置的FIFO队列来完成获取资源线程的排队工作。AQS使用CAS对该同步状态进行原子操作实现对其值的修改。

private volatile int state;//共享变量，使用volatile修饰保证线程可见性

状态信息通过protected类型的getState，setState，compareAndSetState进行操作

//返回同步状态的当前值
protected final int getState() {  return state;
}// 设置同步状态的值
protected final void setState(int newState) { state = newState;
}//原子地（CAS操作）将同步状态值设置为给定值update如果当前同步状态的值等于expect（期望值）
protected final boolean compareAndSetState(int expect, int update) {return unsafe.compareAndSwapInt(this, stateOffset, expect, update);
}

AQS对资源的共享方式

AQS定义两种资源共享方式

Exclusive（独占）：只有一个线程能执行，如ReentrantLock。又可分为公平锁和非公平锁：
公平锁：按照线程在队列中的排队顺序，先到者先拿到锁
非公平锁：当线程要获取锁时，无视队列顺序直接去抢锁，谁抢到就是谁的

Share（共享）：多个线程可同时执行，如Semaphore/CountDownLatch。Semaphore、CountDownLatch、 CyclicBarrier、ReadWriteLock 我们都会在后面讲到。
ReentrantReadWriteLock 可以看成是组合式，因为ReentrantReadWriteLock也就是读写锁允许多个线程同时对某一资源进行读。

不同的自定义同步器争用共享资源的方式也不同。自定义同步器在实现时只需要实现共享资源 state 的获取与释放方式即可，至于具体线程等待队列的维护（如获取资源失败入队/唤醒出队等），AQS已经在顶层实现好了。

AQS低层使用了模板方法模式

同步器的设计是基于模板方法模式的，如果需要自定义同步器一般的方式是这样（模板方法模式很经典的一个应用）：

使用者继承AbstractQueuedSynchronizer并重写指定的方法。（这些重写方法很简单，无非是对于共享资源state的获取和释放）
将AQS组合在自定义同步组件的实现中，并调用其模板方法，而这些模板方法会调用使用者重写的方法。
这和我们以往通过实现接口的方式有很大区别，这是模板方法模式很经典的一个运用。

AQS使用了模板方法模式，自定义同步器时需要重写下面几个AQS提供的模板方法：

isHeldExclusively()//该线程是否正在独占资源。只有用到condition才需要去实现它。
tryAcquire(int)//独占方式。尝试获取资源，成功则返回true，失败则返回false。
tryRelease(int)//独占方式。尝试释放资源，成功则返回true，失败则返回false。
tryAcquireShared(int)//共享方式。尝试获取资源。负数表示失败；0表示成功，但没有剩余可用资源；正数表示成功，且有剩余资源。
tryReleaseShared(int)//共享方式。尝试释放资源，成功则返回true，失败则返回false。

默认情况下，每个方法都抛出 UnsupportedOperationException。 这些方法的实现必须是内部线程安全的，并且通常应该简短而不是阻塞。AQS类中的其他方法都是final ，所以无法被其他类使用，只有这几个方法可以被其他类使用。

以ReentrantLock为例，state初始化为0，表示未锁定状态。A线程lock()时，会调用tryAcquire()独占该锁并将state+1。此后，其他线程再tryAcquire()时就会失败，直到A线程unlock()到state=0（即释放锁）为止，其它线程才有机会获取该锁。当然，释放锁之前，A线程自己是可以重复获取此锁的（state会累加），这就是可重入的概念。但要注意，获取多少次就要释放多么次，这样才能保证state是能回到零态的。

再以CountDownLatch以例，任务分为N个子线程去执行，state也初始化为N（注意N要与线程个数一致）。这N个子线程是并行执行的，每个子线程执行完后countDown()一次，state会CAS(Compare and Swap)减1。等到所有子线程都执行完后(即state=0)，会unpark()主调用线程，然后主调用线程就会从await()函数返回，继续后余动作。

一般来说，自定义同步器要么是独占方法，要么是共享方式，他们也只需实现tryAcquire-tryRelease、tryAcquireShared-tryReleaseShared中的一种即可。但AQS也支持自定义同步器同时实现独占和共享两种方式，如ReentrantReadWriteLock。

AQS组件总结

• Semaphore(信号量)-允许多个线程同时访问： synchronized 和 ReentrantLock 都是一次只允许一个线程访问某个资源，Semaphore(信号量)可以指定多个线程同时访问某个资源。
• CountDownLatch （倒计时器）： CountDownLatch是一个同步工具类，用来协调多个线程之间的同步。这个工具通常用来控制线程等待，它可以让某一个线程等待直到倒计时结束，再开始执行。
• CyclicBarrier(循环栅栏)： CyclicBarrier 和 CountDownLatch 非常类似，它也可以实现线程间的技术等待，但是它的功能比 CountDownLatch 更加复杂和强大。主要应用场景和 CountDownLatch 类似。CyclicBarrier 的字面意思是可循环使用（Cyclic）的屏障（Barrier）。它要做的事情是，让一组线程到达一个屏障（也可以叫同步点）时被阻塞，直到最后一个线程到达屏障时，屏障才会开门，所有被屏障拦截的线程才会继续干活。CyclicBarrier默认的构造方法是 CyclicBarrier(int parties)，其参数表示屏障拦截的线程数量，每个线程调用await()方法告诉 CyclicBarrier 我已经到达了屏障，然后当前线程被阻塞。