蒙特卡洛方法简史

基本概念

相对频率

使用相对概率去估计概率

蒙特卡洛估计器的性质

满足无偏性（即在平均意义下可以得到正确的结果）
满足一致性（样本数目越大，统计值越接近真实值，不允许在真实值附近振荡，即使平均值在趋近真实值）

蒙特卡洛估计

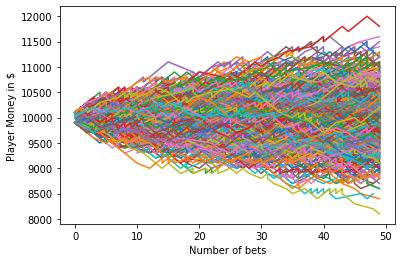
下面展示一个 估计pi的代码。

%
m=input('Enter M, the number of experiments > ');
n=input('Enter N, the number of trials per experiment > ');
z=zeros(1,m);
data = zeros(n,m);
for j=1:mx=rand(1,n);y=rand(1,n);k=0;for i=1:nif x(i)^2+y(i)^2 <= 1		% Fall inside pie slice?k=k+1;enddata(i,j) = 4*(k/i);		% jth estimate of piendz(j) = data(n,j);				% Store data
end
plot(data,'k')						% Plot curves
xlabel('Number of Trials')
ylabel('Estimate of pi')
% End of script file.

3 在通信系统中的应用-AWGN信道

3.1二项式分布

方法：让N个符号通过系统（系统的计算机仿真模型），并计算发送差错的个数Ne。如果在N 次的符号发送中有Ne次差错，则符号差错概率为Ne/N.
例：在差错事件相互独立的情况下，可以用投掷硬币事件来模拟二进制发送.
N个符号的发送可建模为对一枚不均匀硬币进行N次投掷。可以假设第i次投掷结果为“反面”相当于对第i次发送作出正确的判断，而第i次投掷结果为“正面”相当于对此次发送作出错误的判决
因为投掷是相互独立的，所以这个实验模拟了AWGN信道中的二进制数据传输

%
M = 2000;				    % number of experiments
N = 500;					% Number of tosses / experiment
H = zeros(1,M);             % Initialize array
H_theor = zeros(1,M);	    % Initialize array
for j=1:MA = rand(1,N);heads = 0;for k=1:Nif A(k)<=0.2%20%的概率产生正面，正面为错误heads = heads+1;endendH(j) = heads;
end
H_max = max(H); H_min = min(H);
r = H_min:H_max;
[Nb] = hist(H,r);
%
for k=H_min:H_maxH_theor(k) = M*nchoosekN,k)*((0.2)^k)*((0.8)^(N-k));
end
subplot(2,1,1)
hist(H,r)
xlabel('Number of heads')
ylabel('Number of occurences')
subplot(2,1,2)
plot(r,Nb,'ok',r,H_theor(1,H_min:H_max),'k')
xlabel('Number of heads')
ylabel('Number of occurences')
% End of script file.