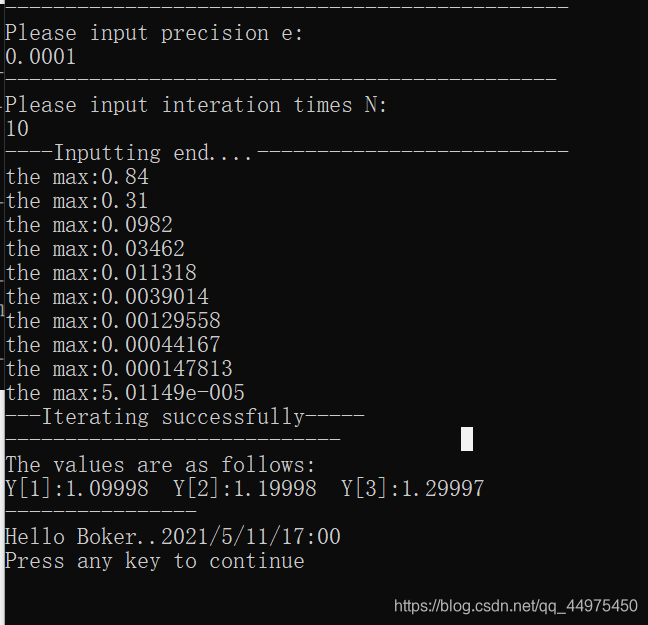
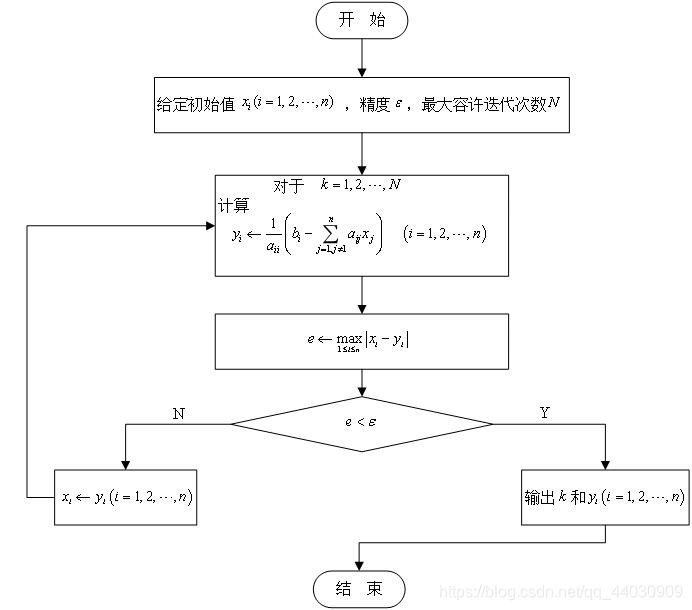
雅可比迭代法解线性方程组。

article/2025/4/22 2:57:03

watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAYW1lbl95YW53YW5n,size_15,color_FFFFFF,t_70,g_se,x_16

L U分解在我之前写的文章里。

定义的变量有点多，但挺容易看的。

#include<stdio.h>
#include<math.h>
#define N 3 
int main (void)
{double A[N][N] = {0};double D[N][N] = {0};double L[N][N] = {0};double U[N][N] = {0};double C[N][N] = {0};double H[N][N] = {0};double B[N][N] = {0};double F[N][N] = {0};double F1[N][N] = {0};double X[N][N] = {0};double X1[N][N] = {0};double X2[N][N] = {0};double X3[N][N] = {0};double X4[N][N] = {0};double sum1 = 0;int i,j,k;printf("请输入你的矩阵A：\n");for(i = 0;i<N;i++){printf("第%d行：",i+1);for(j=0;j<N;j++){scanf("%lf",&A[i][j]);}}printf("\n");printf("请输入你的常数矩阵：\n");for(i = 0;i<N;i++){printf("第%d行：",i+1);for(j=0;j<N;j++){scanf("%lf",&B[i][j]);}}printf("\n");printf("请输入你的矩阵U：\n");for(i = 0;i<N;i++){printf("第%d行：",i+1);for(j=0;j<N;j++){scanf("%lf",&U[i][j]);}}printf("\n");printf("请输入你的矩阵L：\n");for(i = 0;i<N;i++){printf("第%d行：",i+1);for(j=0;j<N;j++){scanf("%lf",&L[i][j]);}}printf("\n");/*以迹组成的矩阵D的逆矩阵*/for(i = 0;i<N;i++){D[i][i] = 1/A[i][i];}/*矩阵L+U = H*/for(i = 0;i<N;i++){for(j=0;j<N;j++){H[i][j] = L[i][j] + U[i][j];}}/*以迹组成的矩阵D的逆矩阵与矩阵L+U = H的乘积矩阵C*/for(i = 0;i<N;i++){for(j = 0;j<N;j++){for(k=0;k<N;k++){C[i][j] += D[i][k]*H[k][j];}}}/*以迹组成的矩阵D的逆矩阵与系数矩阵的乘积新的系数矩阵F*/for(i = 0;i<N;i++){for(j = 0;j<N;j++){for(k=0;k<N;k++){F[i][j] += D[i][k]*B[k][j];}}}for(i = 0;i<N;i++){F1[i][0] = F[i][0];}sum1 = 1;while(sum1 > 0.0001){for(i = 0;i<N;i++){for(j=0;j<N;j++){X1[i][j] = 0;X2[i][j] = 0;X3[i][j] = 0;X4[i][j] = 0;}}sum1 = 0;/*乘积矩阵C与初值矩阵X的新乘积矩阵X1*/for(i = 0;i<N;i++){for(j = 0;j<N;j++){for(k=0;k<N;k++){X1[i][j] += C[i][k]*X[k][j];}}}/*新乘积矩阵X1的第一列矩阵X2*/for(i = 0;i<N;i++){X2[i][0] = X1[i][0];}/*核心雅可比迭代公式*/for(i = 0;i<N;i++){for(j = 0;j<N;j++){X3[i][j] = X2[i][j] + F1[i][j];}}/*判断是否需要继续迭代*//*新初值矩阵X3与原始初值矩阵X的差矩阵X4，X3与X仅有第一列元素被赋值为非0*/for(i = 0;i<N;i++){for(j = 0;j<N;j++){X4[i][j] = X3[i][j] - X[i][j];}}/*差矩阵X4的二范数*/for(i = 0;i<N;i++){sum1 += X4[i][0]*X4[i][0];}sum1 = sqrt(sum1);/*把新初值矩阵赋给原始初值矩阵，代替其位置。*/for(i = 0;i<N;i++){for(j = 0;j<N;j++){X[i][j] = X3[i][j];}}}printf("最终利用雅可比迭代法求得的线性方程组的解是：\n");for(i = 0;i<N;i++){printf("%lf\t",X3[i][0]);}printf("\n");return 0;}That's all！？

watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAYW1lbl95YW53YW5n,size_11,color_FFFFFF,t_70,g_se,x_16