雅可比迭代法、高斯-赛德尔迭代法、超松弛迭代法 matlab 实现

一、雅可比迭代法

程序代码：

function y = Jacobi(A,b,e,M)
% input: A 的对角线元素均不为 0	e: 精度	M: 最大计算次数
% output: y: 方程的解n = length(A);
x0 = zeros(n,1);
y = zeros(n,1);[l,w] = size(A);
if (l ~= w) && (l ~= length(b))disp('输入错误');
end% ---------------------------
% 矩阵形式
% D = diag(diag(A),0);
% U = triu(-A,1); %上三角矩阵
% L = tril(-A,-1); %下三角矩阵
% B = inv(D)*(L+U);
% f = inv(D)*b;
% for i = 1:M
%     y = B*x0+f;
%     d = abs(x0-y);
%     if(max(d)<e)
%         break;
%     end
%     x0 = y;
% end
% ---------------------------% ---------------------------
% 多项式形式
D = diag(A);
for i = 1:Mfor j = 1:ny(j) = 1/D(j)*(b(j)-A(j,1:j-1)*x0(1:j-1)-A(j,j+1:n)*x0(j+1:n));endd = abs(x0-y);if(max(d)<e)break;endx0 = y;
end
% ---------------------------
end

矩阵形式和多项式形式分别是算法的两种实现，且两种方法等价，选择一种运行即可！
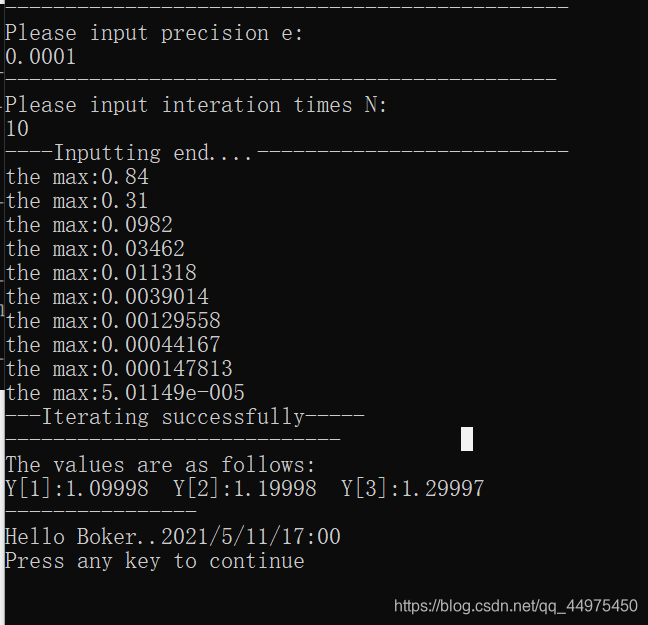
测试：

在这里插入图片描述

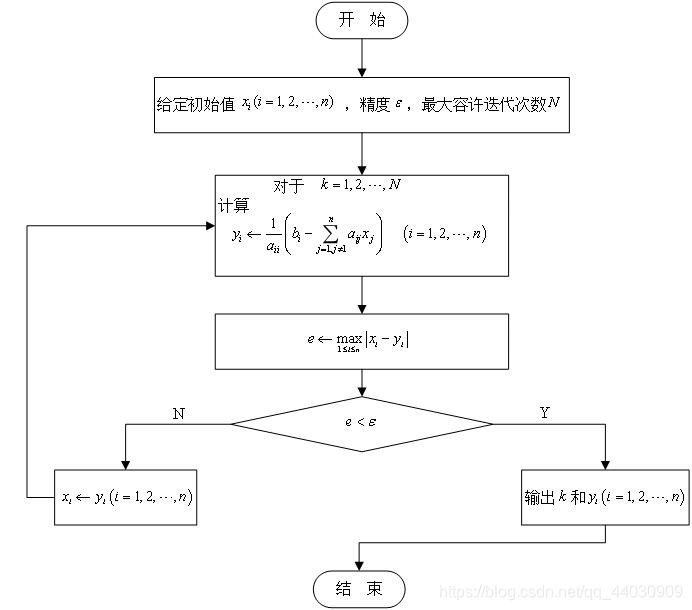
二、高斯-塞德尔迭代法

程序代码：

function y = G_S(A,b,e,M)
% input: A 的对角线元素均不为 0	e: 精度	M: 最大计算次数
% output: y: 方程的解n = length(A);
x0 = zeros(n,1);
y = zeros(n,1);[l,w] = size(A);
if (l ~= w) && (l ~= length(b))disp('输入错误');
end% ---------------------------
% 矩阵形式
% D = diag(diag(A),0);
% U = triu(-A,1); %上三角矩阵
% L = tril(-A,-1); %下三角矩阵
% B = inv(D-L)*U;
% f = inv(D-L)*b;
% for i = 1:M
%     y = B*x0+f;
%     d = abs(x0-y);
%     if(max(d)<e)
%         break;
%     end
%     x0 = y;
% end
% ---------------------------% ---------------------------
% 多项式形式
D = diag(A);
for i = 1:Mfor j = 1:ny(j) = 1/D(j)*(b(j)-A(j,1:j-1)*y(1:j-1)-A(j,j+1:n)*x0(j+1:n));endd = abs(x0-y);if(max(d)<e)break;endx0 = y;
end
% ---------------------------
end

矩阵形式和多项式形式分别是算法的两种实现，且两种方法等价，选择一种运行即可！
测试：

在这里插入图片描述

三、超松弛迭代法

程序代码：

function y = SOR(A,b,r,e,M)
% input: A 的对角线元素均不为 0	r: 松弛因子	e: 精度	M: 最大计算次数
% output: y: 方程的解n = length(A);
x0 = zeros(n,1);
y = zeros(n,1);
y_bar = zeros(n,1);[l,w] = size(A);
if (l ~= w) && (l ~= length(b))disp('输入错误');
end% ---------------------------
% 矩阵形式
% D = diag(diag(A),0);
% U = triu(-A,1); %上三角矩阵
% L = tril(-A,-1); %下三角矩阵
% B = inv(D-r*L)*((1-r)*D+r*U);
% f = r*inv(D-L)*b;
% for i = 1:M
%     y = B*x0+f;
%     d = abs(x0-y);
%     if(max(d)<e)
%         break;
%     end
%     x0 = y;
% end
% ---------------------------% ---------------------------
% 多项式形式
D = diag(A);
for i = 1:Mfor j = 1:ny_bar(j) = 1/D(j)*(b(j)-A(j,1:j-1)*y(1:j-1)-A(j,j+1:n)*x0(j+1:n));y(j) = (1-r)*x0(j)+r*y_bar(j);endd = abs(x0-y);if(max(d)<e)break;endx0 = y;
end
% ---------------------------
end

矩阵形式和多项式形式分别是算法的两种实现，且两种方法等价，选择一种运行即可！
测试：

在这里插入图片描述