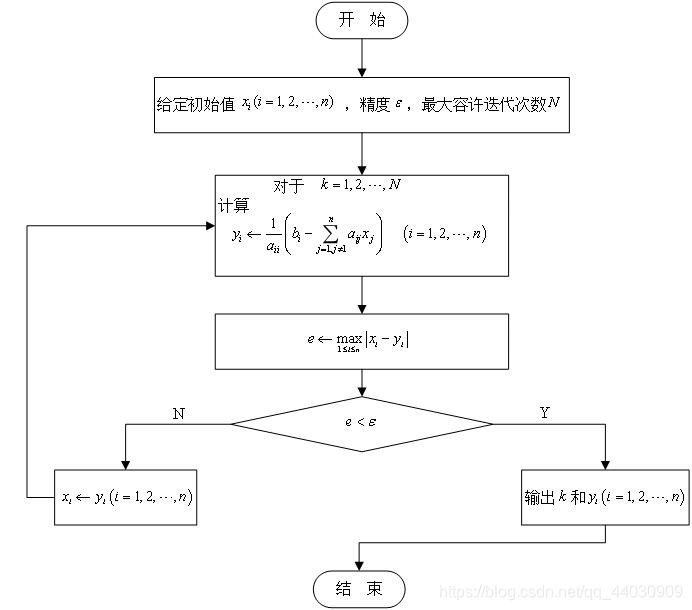
计算方法实验，在已给matlab的程序基础上进行修改得到的python程序，原理不再赘述。实际使用时，只需修改以下程序中的A,b矩阵（注意只适用与A为n*n的情况）

1.雅克比迭代法

import numpy as npA = np.array([[10,-1,-2],[-1,10,-2],[-1,-1,5]],dtype = float)
b = np.array([[72],[83],[42]],dtype = float)
n = A.shape[0]err = 1
eps = 0.00001
N=100
iter = 0
solution =np.zeros(n)while err>eps and iter<N:iter=iter+1x0=solution.T.copy()for i in range(0,n):t= np.matmul(A[i,:],x0)solution[i]= np.matmul(A[i,:],x0)m =A[i,i]*x0[i]solution[i]=(b[i]-solution[i]+A[i,i]*x0[i])/A[i,i]err=max(abs(solution-x0))if iter==N:print('迭代次数达到允许上限')
else:print('雅可比迭代法迭代次数为：',iter)print('结果为：',solution)

2、高斯-赛德尔迭代法

import numpy as npA = np.array([[10, -1, -2], [-1, 10, -2], [-1, -1, 5]], dtype=float)
b = np.array([[72], [83], [42]], dtype=float)
n = A.shape[0]err = 1
eps = 0.00001
N = 100
iter = 0
solution = np.zeros(n)
while err > eps and iter < N:iter = iter + 1x0 = solution.T.copy()for i in range(n):solution[i] =np.matmul(A[i, 0:i],solution[0: i].copy()) +np.matmul(A[i, i + 1: n],x0[i + 1: n].copy())solution[i] = (b[i] - solution[i]) / A[i, i]err = max(abs(solution - x0))if iter == N:print('迭代次数达到允许上限')
else:print('高斯迭代法迭代次数为：',iter)print('结果为：',solution)

 

4、超松弛迭代法

import numpy as npA = np.array([[10, -1, -2], [-1, 10, -2], [-1, -1, 5]], dtype=float)
b = np.array([[72], [83], [42]], dtype=float)
n = A.shape[0]err = 1
eps = 0.00001
N = 100
iter = 0
solution = np.zeros(n)def chaosongchi(err,eps,iter,A, b, w):while err > eps and iter < N:iter = iter + 1x0 = solution.T.copy()for i in range(n):solution[i] = np.matmul(A[i, 0:i], solution[0: i].copy()) + np.matmul(A[i, i + 1: n],x0[i + 1: n].copy()) solution[i] = (b[i] - solution[i]) / A[i, i]solution[i] = (1 - w) * x0[i].copy() + w * solution[i].copy()err = max(abs(solution - x0))  if iter == N:print('迭代次数达到允许上限')else:print('当松弛因子为：',w)print('超松弛迭代法迭代次数为：', iter)print('结果为：', solution)chaosongchi(err,eps,iter,A,b,1)#最后一个参数为松弛因子