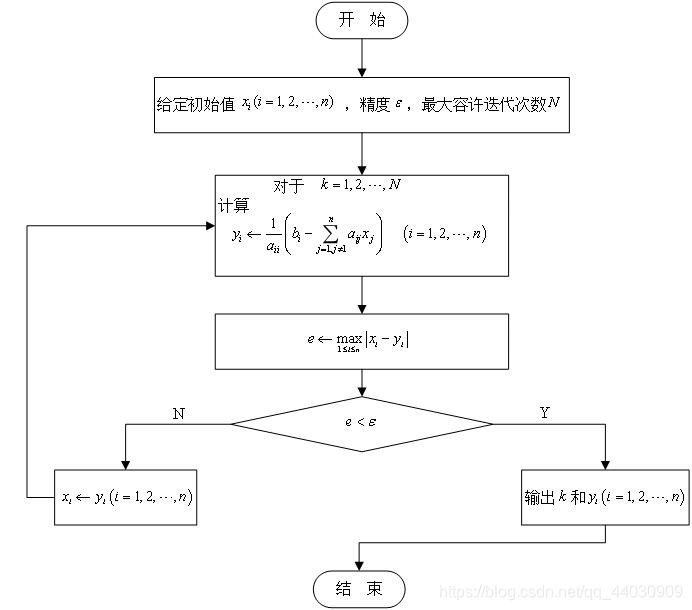
数值计算——雅可比迭代法解线性方程组

article/2025/4/22 3:18:56

1.雅克比迭代法的计算过程:

(1).取初始向量:

$x^{(0)}=(x_{1}^{(0)},x_{2}^{(0)},\cdots ,x_{n}^{(0)})^{T}$ （1）

(2).迭代过程

$\left\{\begin{matrix} x_{1}^{(k+1)}=\frac{1}{a_{11}}\left ( -a_{12}x_{2}^{(k)}-\cdots -a_{1n}x_{n}^{(k)}+b_{1}\right )\\ x_{2}^{(k+1)}=\frac{1}{a_{22}}\left ( -a_{21}x_{1}^{(k)}-\cdots -a_{2n}x_{n}^{(k)}+b_{2}\right ) \\ \vdots \\ x_{n}^{(k+1)}=\frac{1}{a_{nn}}\left ( -a_{n1}x_{1}^{(k)}-\cdots -a_{nn-1}x_{n-1}^{(k)}+b_{n}\right ) \end{matrix}\right.$ （2）

2.求解实例：

$\begin{bmatrix} 3 & -1 & & & \\ -1 & 3 & -1 & & \\ & \ddots & \ddots & \ddots & \\ & & -1 & 3 & -1 \\ & & & -1 & 3 \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ \vdots \\ x_{n-1}\\ x_{n} \end{bmatrix}=\begin{bmatrix} 2\\ 1\\ \vdots \\ 1\\ 2 \end{bmatrix}$ （3）

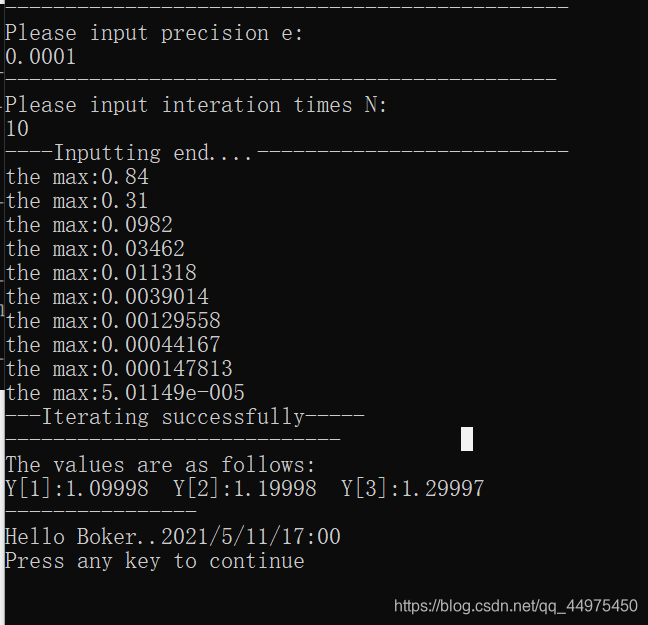
用 Jacobi 方法求解，精确到小数点后 6 位, 给出所需步数及残差 $\left \| b-Ax \right \|_{\infty }$ ;

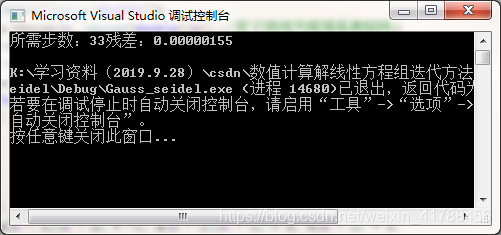
3.求解结果：

当n=100时，x1...xn=1,所需步数33，残差0.00000155

//雅克比迭代法，解线性方程组，高等数值计算
//#include "pch."
#include <iostream>
using namespace std;
#include <iomanip> //参数化输入/输出 
#include <vector>
#define  n  100    //矩阵大小
#define  epsilon  0.001   //精度
vector<double> jacobi(vector<vector<double>>a, vector<double>b, vector<double>x_new);//申明雅克比迭代方法求解函数
vector<double> jacobi(vector<vector<double>>a, vector<double>b, vector<double>x_new)
{int num = size(b), n_cishu = 0;double sum = 0, max_precision = 0;;vector<double>x_old(num);do{n_cishu++;for (int j = 0; j < num; j++){x_old[j] = x_new[j];}for (int j = 0; j < num; j++){sum = 0;for (int k = 0; k < num; k++){if (j != k){sum = sum - a[j][k] * x_old[k];}}x_new[j] = (sum + b[j]) / a[j][j];max_precision = 0;for (int i = 0; i < num; i++){sum = fabs(x_new[i] - x_old[i]);if (sum > max_precision){max_precision = sum;}}}} while (max_precision > epsilon);//残差计算double max_residual = 0;for (int i = 0; i < num; i++){sum = b[i];for (int j = 0; j < num; j++){sum = sum - a[i][j] * x_new[j];}if (sum > max_residual){max_residual = sum;}}//cout << "所需步数：" << n_cishu << "残差：" << fixed << setprecision(8) << setw(10) << max_residual << endl;return x_new;
}
int main()
{vector<vector<double>>a;a.resize(n, vector<double>(n));//定义线性方程组系数矩阵Avector<double>b(n);  //定义线性方程组右边列向量Bvector<double>x(n);  //初始化向量a[0][0] = 3, a[0][1] = -1, b[0] = 2;for (int i = 1; i < n - 1; i++){a[i][i - 1] = -1;a[i][i] = 3;a[i][i + 1] = -1;b[i] = 1;}a[n - 1][n - 2] = -1; a[n - 1][n - 1] = 3, b[n - 1] = 2;x = jacobi(a, b, x);for (int i = 0; i < n; i++)cout << x[i] << endl;
}