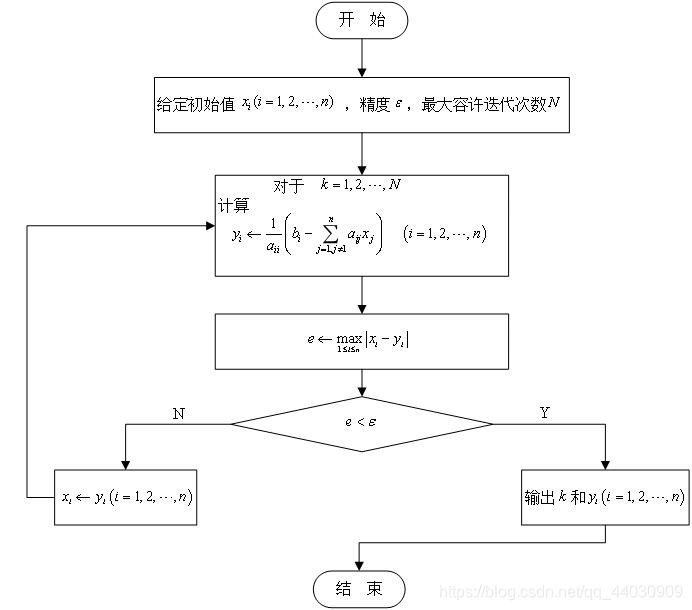
文章目录
- 一、基本迭代法的格式及收敛性
- 1.1 迭代法思想
- 1.2 向量序列收敛的定义
- 二、迭代法的收敛与发散
- 三、雅可比迭代法和高斯赛德尔迭代法
- 3.1 雅可比迭代法
- 3.2 高斯――赛得尔(Gauss-Seidel)迭代法
- 四、迭代法的收敛性
- 4.1 严格对角占优矩阵与对角占优矩阵
- 4.2 Jacobi迭代法和Gauss-Seidel迭代法的收敛性
一、基本迭代法的格式及收敛性
1.1 迭代法思想

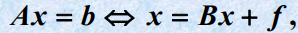
- 基本迭代法的迭代格式

- 例题


- 结论
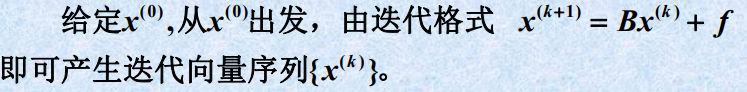

1.2 向量序列收敛的定义

- 例题
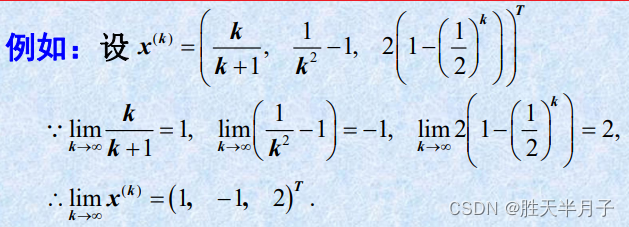
- 结论

二、迭代法的收敛与发散
- 引例



三、雅可比迭代法和高斯赛德尔迭代法
3.1 雅可比迭代法
以下原理性东西了解即可,通过例题明白如何计算怎么计算就可以
- 原理

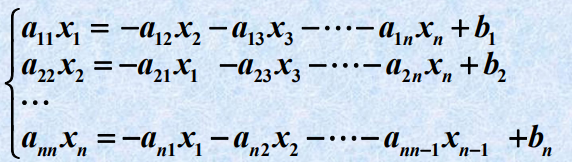
第 i 个 方 程 除 以 a i i ( i = 1 , 2 , … , n ) , 得 : 第i个方程除以a_{ii}(i =1,2,…,n),得: 第i个方程除以aii(i=1,2,…,n),得:
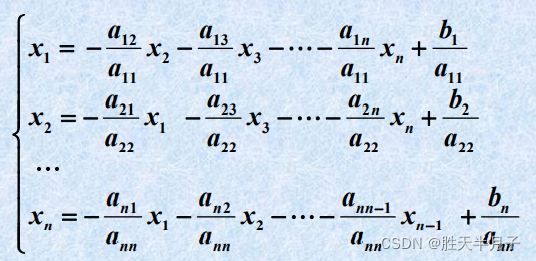
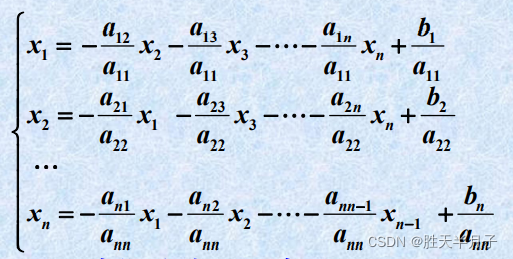
Jacobi迭代的分量形式
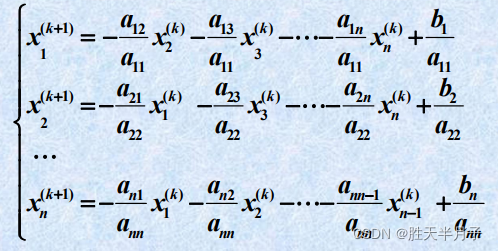
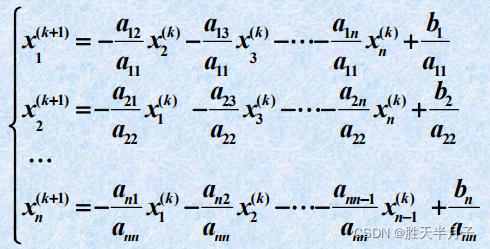
即得到计算公式(雅可比迭代法) :对 k = 0 , 1 , … k=0,1,… k=0,1,…
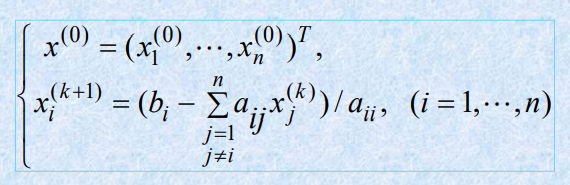
- 例题



Jacobi迭代用9次迭代,基本得到该题的精确解。 - 雅可比迭代法的收敛性
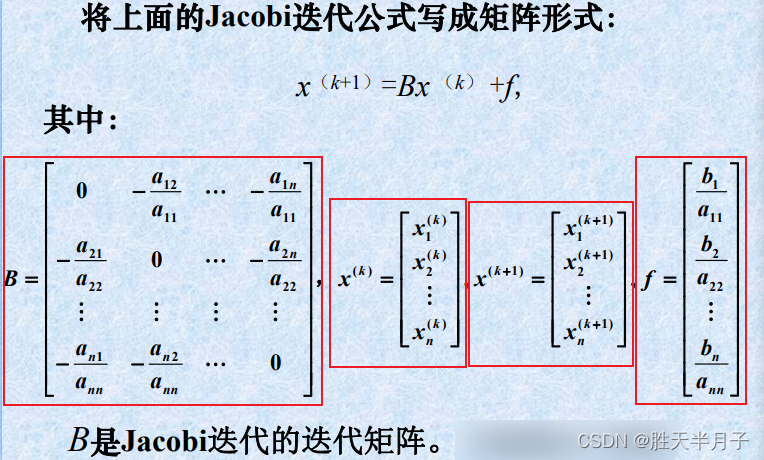
下面给出一种更方便的形式:

- 雅可比迭代的矩阵表示

3.2 高斯――赛得尔(Gauss-Seidel)迭代法
- 原理

- 对比⭐

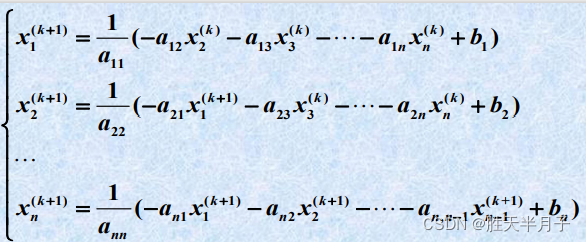
- 高斯—塞德尔迭代公式:
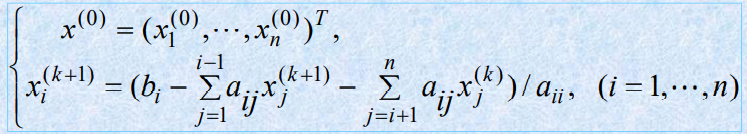
- 高斯—塞德尔迭代的矩阵表示


- 例题

雅可比:
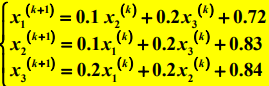
高斯—塞德尔迭代法得如下迭代公式:
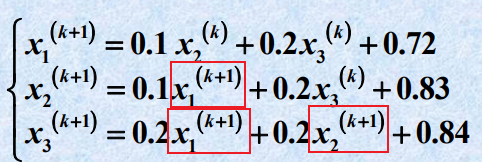
- 结论

四、迭代法的收敛性
4.1 严格对角占优矩阵与对角占优矩阵
- 概念

- 谱半径
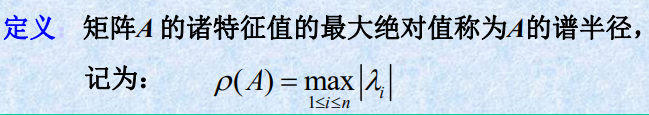
4.2 Jacobi迭代法和Gauss-Seidel迭代法的收敛性
- 定理1
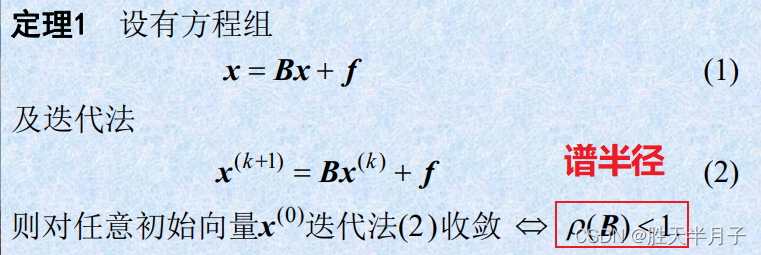

- 例题
-
定理2

正定矩阵:对于具体的实对称矩阵,常用矩阵的各阶顺序主子式是否大于零来判断其正定性;(求出A的所有特征值。若A的特征值均为正数,则A是正定的;) -
例题


-
定理3

-
定理4

-
例题

-
结论