一、 实验目的
使用matlab编程,利用蒙特卡洛方法,对一个简单的二元假设检验问题进行仿真,分析不同信噪比下检测器的性能,分析SNR、MSE对估计的影响。
二、 实验步骤
通过蒙特卡洛仿真实验,检测性能在不同信噪比下的表现,以验证信噪比对于检测性能的影响。
实验步骤:
- 根据给定的参数设置,生成信号 s 和噪声 w ,并将它们相加得到观测数据 x 。
- 对于每一个待估计频率 f ,计算对数似然函数 log L ( f )的值,并找到最大值对应的 f 值作为 MLE 的结果f 。
- 计算 MLE 的均方误差(MSE),即(f − f 0 )² 的平均值。
- 计算 CRB 的值,并与 MLE 的 MSE 进行比较。
- 重复上述步骤多次(本实验中重复 5000 次),并绘制 MLE 和 CRB 随 SNR 变化的曲线图。
三、 实验原理
假设观测到一个长度为 N 的信号 s ,其形式为:
![]() (3-1)
(3-1)
其中f0 是信号频率, n是时域采样点, w 是加性高斯白噪声,其方差为 σ² ,信噪比(SNR)定义为:
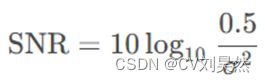 (3-2)
(3-2)
本实验中,信号长度 N = 20 ,信号频率 f0 =0.2565,信噪比 SNR 在 -6 到 8 dB 之间变化,待估计频率 f 在 0.001 到 0.499 之间变化。
3.1 MLE
对于给定的观测数据 s ,其对数似然函数为:
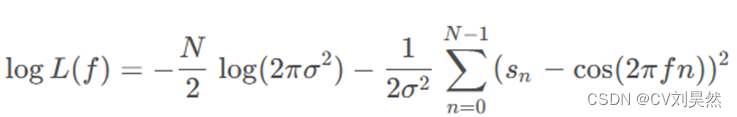 (3-3)
(3-3)
MLE 的思想是找到使得对数似然函数最大化的 f 值,即:
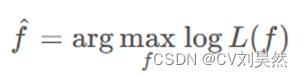 (3-4)
(3-4)
由于对数似然函数是关于 f 的非线性函数,无法直接求解出解析解,因此需要采用数值方法来求解。本实验中,使用了遍历搜索法,即在给定的 f 范围内,逐点计算对数似然函数的值,并找到最大值对应的 f 值作为 MLE 的结果。
3.2 CRB
CRB 是一种评价无偏估计器性能的指标,它给出了无偏估计器方差的下界,即:
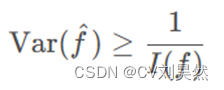 (2-5)
(2-5)
其中 I(f)是费舍尔信息量,定义为:
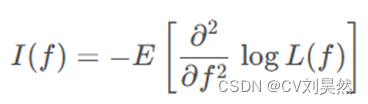 (2-6)
(2-6)
对于本实验中的信号模型,可以推导出:
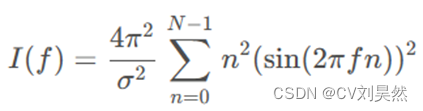 (2-6)
(2-6)
因此,CRB 可以表示为:
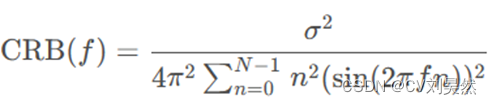 (2-7)
(2-7)
四、Matlab实现
Matlab代码实现如下:
| %%参数区 N =20; % 信号长度 f0 = 0.2565; % 信号频率 SNR0=-6:2:8; % 信噪比范围 sigma2=0.5./10.^(SNR0/10); % 噪声方差 f = 0.001:0.001:0.499; % 待估计频率范围 % CRB和IMLE for i = 1:length (sigma2) s = cos(2*pi*f0*[0:N-1]); % 生成信号 SNR(i)=10*log10(0.5/sigma2(i)); % 计算信噪比 CRB(i) = sigma2(i)/(4*pi^2*sum([0:N-1].^2.*(sin(2*pi*f0*[0:N-1])).^2)); % 计算CRB for mc = 1:5000 % 蒙特卡洛仿真次数 x = s + sqrt (sigma2 (i)) *randn(N,1).'; % 生成含噪声信号 for j=1:length(f) J1(i,j)=sum((x-cos(2*pi*f(j)*[0:N-1])).^2); % 计算似然函数 end u1 = find(J1(i,:) == min(J1(i,:))); % 找到似然函数最小值对应的频率 mle(mc,i) = (f(u1)-f0).^2; % 计算MLE end MLE(i)=sum(mle(:,i)/mc); % 计算MSE end %%plot figure(1) semilogy(SNR,(MLE),'r-s'); % 绘制MLE曲线 hold on semilogy(SNR,(CRB),'b-+'); % 绘制CRB曲线 xlabel('SNR'),ylabel('MSE') legend('MLE','CRB') % 添加图例 |
五、实验结果
通过蒙特卡洛仿真实验,可以发现:在频率估计中,CRB是一个理论上的下界,而MLE是一种常用的实际估计方法。在信噪比较低的情况下,MLE的MSE较高,估计结果不够准确;而在信噪比较高的情况下,MLE的MSE逐渐接近CRB,估计结果更加准确。因此,在实际应用中,需要根据具体情况选择合适的估计方法。。
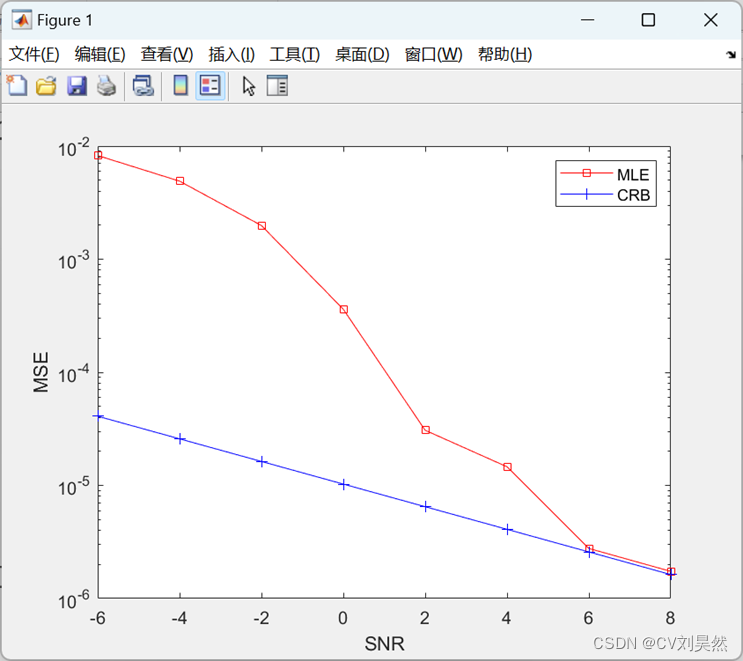
图 5-1 SNR-MSE曲线图