一、 实验目的
使用matlab编程,利用蒙特卡洛方法,对一个简单的二元假设检验问题进行仿真,分析不同信噪比下检测器的性能。
二、 实验步骤
通过蒙特卡洛仿真实验,检测性能在不同信噪比下的表现,以验证信噪比对于检测性能的影响。
实验步骤:
1. 设置随机数种子为0,定义参数N=20,M=5000,A=1,SNR = [-15,-10,-5,0,5]。
2. 根据信噪比计算噪声方差sig2,其中SNR = 101og10(A. 2/sig2)。
3. 对于每个信噪比SNR,进行M次实验。
4. 对于每次实验,生成随机噪声n,计算H0下的GLR值和H1下的GLR值。
5. 对于H0下的GLR值,按照升序排序,并计算出不同Pfa下的阈值T。
6. 对于每个阈值T,计算出Pd值,绘制Pfa-Pd曲线。
7. 重复以上步骤,绘制不同信噪比下的Pfa-Pd曲线。
三、 实验原理
3.1 假设检验
假设检验问题是指根据观测数据,判断某个未知参数或状态属于两个或多个可能的假设中的哪一个。本实验考虑一个二元假设检验问题,即只有两个假设:H0和H1。
假设观测数据为x,它是一个长度为N的向量,每个元素都是一个随机变量。
在H0假设下,x只包含高斯白噪声n;
在H1假设下,x包含一个恒定幅值为A的信号和高斯白噪声n。即:
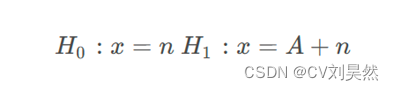
其中,n服从均值为0,方差为σ2的高斯白噪声。
我们观测到N个采样点x = ( x1 , x2 , . . . , xN ),并且假设A和σ 2都是未知参数。那么,在H0和H1下,x的概率密度函数分别为:

根据GLRT的原理,我们需要找到使似然函数最大化的参数A 和σ2 ,并计算两个假设下的最大似然函数值Λ0 和Λ1

那么,广义似然比(GLR)就是Λ0 和Λ1 之比,即
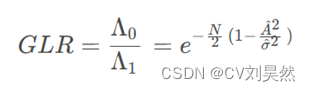
为了进行二元假设检验,我们需要设置一个阈值T,使得当GLR>T时判决为H0成立,否则判决为H1成立。这样,我们就可以计算在给定阈值T下,发生假警和漏警的概率。
虚警概率(Pfa)是指在H0成立时错误地判决为H1成立的概率;
漏警概率(Pmd)是指在H1成立时错误地判决为H0成立的概率;
检测概率(Pd)是指在H1成立时正确地判决为H1成立的概率,即Pd=1-Pmd。
由于x是随机变量,所以GLR也是随机变量。因此,在理论上很难求出Pfa和Pd与T之间的精确关系。这时候,我们就可以利用蒙特卡洛仿真方法来进行数值模拟。
四、matlab实现
| % 设定随机数种子为0,保证每次运行结果一致 randn ('seed', 0); % 信号长度 N=20; % 模拟次数 M=5000; % 信号幅值 A=1; % 信噪比(dB) SNR = [-15,-10,-5,0,5]; % 计算信噪比对应的方差 sig2 = A.^2./(10.^(SNR/10)); % 遍历不同信噪比 for k =1: length (SNR) % 模拟M次 for i=1:M % 生成高斯白噪声(H0) n = sig2(k)*randn(1, N); x0 = n; u0 = mean (x0); % 估计H0下的信号方差 Sig_H0 = 1/N*sum(x0.^2); % 估计H1下的信号方差(MLE方法) Sig_H1 = 1/N*sum((x0-u0).^2); % 计算GLR统计量(H0下) GLR0(i)=Sig_H0/Sig_H1;
% 生成有信号的高斯白噪声(H1) x1=A+n; u1=mean(x1); % 估计H0下的信号方差 Sig_H0 = 1/N*sum(x1.^2); % 估计H1下的信号方差(MLE方法) Sig_H1 = 1/N*sum((x1-u1).^2); % 计算GLR统计量(H1下) GLR1(i) =Sig_H0/Sig_H1; end % 生成Pfa的取值范围 Pfa=linspace (10^-3,1,300); % 对GLR0进行降序排序 GLR0=sort(GLR0,'descend'); % 计算阈值T T=GLR0(ceil (Pfa*M)); % 计算Pd for i=1:length(T) Pd(i) =length (find (GLR1>T(i)))/M; end % 绘制ROC曲线 semilogx(Pfa, Pd,'r*') hold on xlabel ('Pfa'); ylabel ('Pd'); end |
五、实验结果
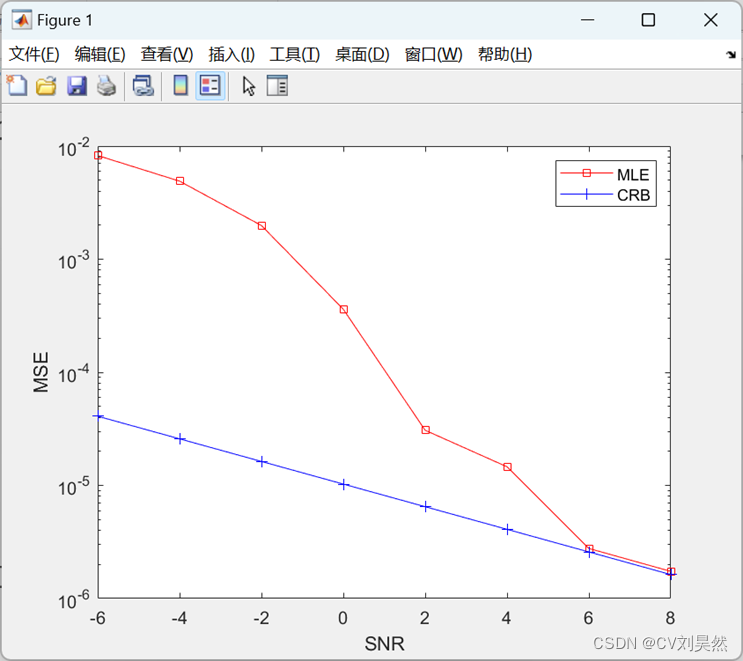
通过蒙特卡洛仿真实验,得到了不同信噪比下的Pfa-Pd曲线,如下图所示,从图中可以看出,随着信噪比的增加,Pd值逐渐增加,Pfa值逐渐减小,检测性能逐渐提高。

图 5-1 pfa-pd曲线图