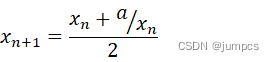1. 概述
牛顿迭代法 牛顿迭代法 牛顿迭代法 是非常高效的求解方程的根的方法。其求解原理可以参考各文献。大体的思路如下:
通过不断地做切线来逼近真实的根,直到误差小于精度。
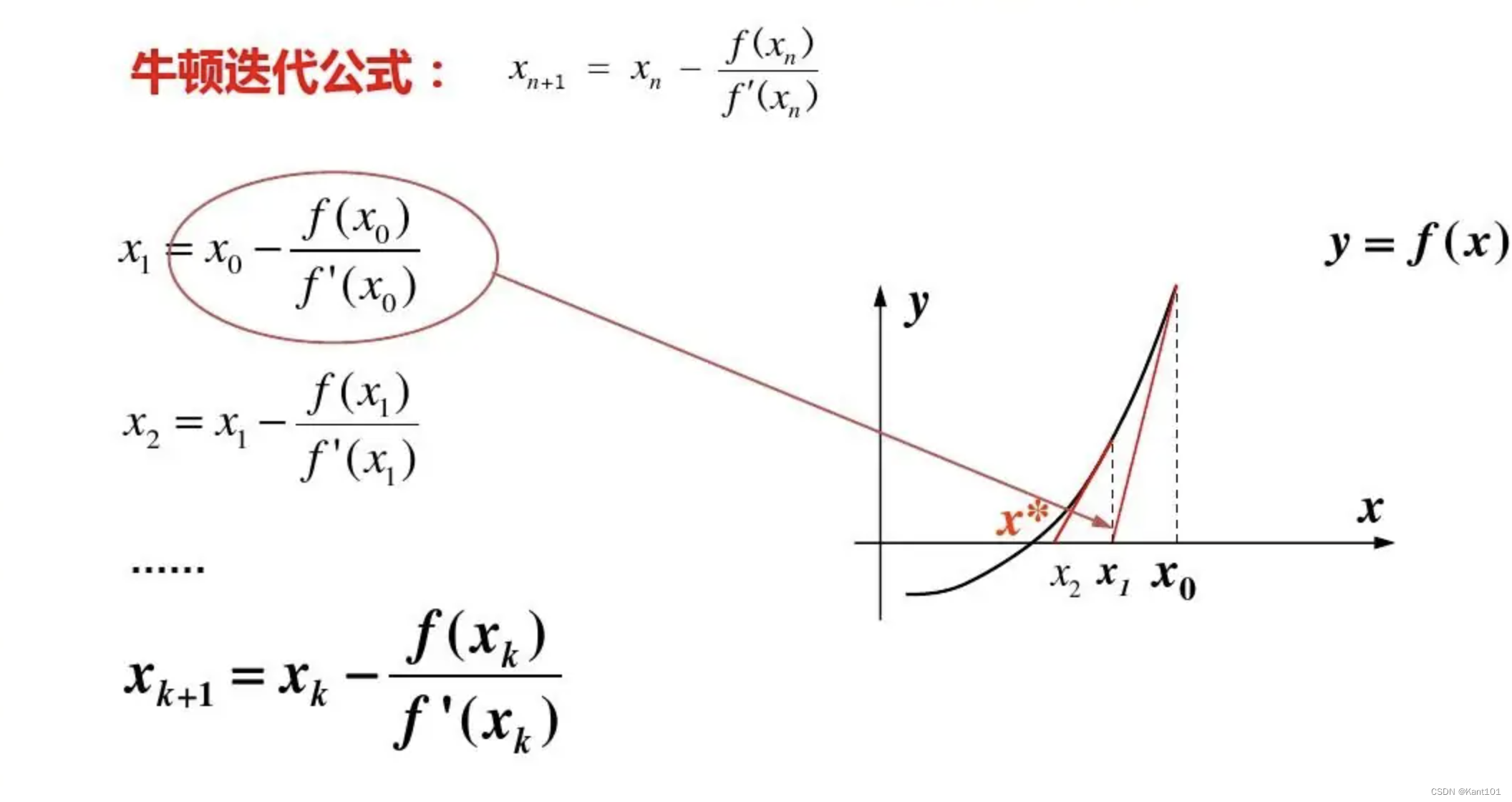
可得迭代公式:
x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} xn+1=xn−f′(xn)f(xn)
通过这种不断地做切线的方法,直到 ∣ x n − x ∗ ∣ < 给定的精度 |x_n - x_*| < 给定的精度 ∣xn−x∗∣<给定的精度,在误差范围内可以认为 x n x_n xn 就是方程的根了。
2. 牛顿法求平法根
假设我们要求解n的平方根,那么我们可以构建函数 f ( x ) = x 2 − n f(x)=x^2-n f(x)=x2−n。
那么方程 x 2 − n = 0 x^2-n=0 x2−n=0 的理论根为 x = n x=\sqrt{n} x=n ,即求解这个方程得到的根就是求的n的平方根。
例如求5的平方根,那么可以构建函数 f ( x ) = x 2 − 5 f(x)=x^2-5 f(x)=x2−5,方程 x 2 − 5 = 0 x^2-5=0 x2−5=0 的理论根即为 5 \sqrt{5} 5,在误差范围内,用牛顿法求解出方程 x 2 − 5 = 0 x^2-5=0 x2−5=0 的根即可认为是5的平方根。
迭代公式
构建函数
f ( x ) = x 2 − n f(x)=x^2-n f(x)=x2−n
那么有:
f ′ ( x ) = 2 x f'(x)=2x f′(x)=2x
根据牛顿法的迭代公式有:
x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} xn+1=xn−f′(xn)f(xn)
= x n − x n 2 − n 2 x n \quad \quad =x_n-\frac{x_n^2-n}{2x_n} =xn−2xnxn2−n
= x n + n / x n 2 \quad\quad =\frac{x_n+n/x_n}{2} =2xn+n/xn
代码
/*** @author allen* @date 2022/9/19*/
public class Main2 {public static void main(String[] args) {double n = 987654321;double x = 0.0000001;double res = sqrt(n, x);System.out.println(res);}public static double sqrt(double n, double x) {double k = n / 2;while (Math.abs(k * k - n) > x) {k = (k + n / k) / 2;}return k;}
}

Python3库函数求平方根验证

3. 牛顿法求多次方根
跟求平方根同理,只是构建的函数不同,例如求解m次方根,那么就需要构建函数
f ( x ) = x m − n f(x)=x^m-n f(x)=xm−n
那么就有:
f ′ ( x ) = m ∗ x m − 1 f'(x)=m*x^{m-1} f′(x)=m∗xm−1
根据牛顿法的迭代公式有:
x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} xn+1=xn−f′(xn)f(xn)
= x n − x n m − n m ∗ x n m − 1 \quad\quad =x_n-\frac{x_n^m-n}{m*x_n^{m-1}} =xn−m∗xnm−1xnm−n
例如求解n的3次方根,那么就有:
x n + 1 = x n − x n 3 − n 3 ∗ x n 2 x_{n+1}=x_n-\frac{x_n^3-n}{3*x_n^2} xn+1=xn−3∗xn2xn3−n
代码
package cn.pku.edu.algorithm;/*** @author allen* @date 2022/9/19*/
public class Main2 {public static void main(String[] args) {double n = 123456789;double x = 0.0000001;double res = sqrt3(n, x);System.out.println(res);}public static double sqrt3(double n, double x) {double k = n / 3;double k2, k3;do {k2 = k * k;k3 = k2 * k;k = k - (k3 - n) / (3 * k2);} while (Math.abs(k * k * k - n) > x);return k;}
}
Python3验证123456789开3次方的结果为

参考文献
[1] 牛顿迭代法.