UML的简单使用

（本文参考文献 《java多线程设计模式》--结城 浩 《java多线程编程实战指南》--黄文海）

一、综述

UML（Unified Modeling Language，统一建模语言）是软件工程领域一种标准化通用图形化建模语言，它被设计用于以可视化的方式来描述软件系统。它是站在可视化的观点来看待程序系统，将规格和重点写下来的表现形式。

UML定义的图形可以分为结构型（Structural UML Diagram）和行为型（Behavioral UML Diagram）

结构型UML包括：类图、组件图、复合结构图、部署图、对象图、包图、轮廓图。

行为型UML包括：活动图、通信图、交互概览图、序列图、状态图、时限图和用例图。

 

关于绘制UML图的方法：我只提供建议，白嫖党可以参考。1.免费的在线绘制网站（本人比较喜欢） firstblood - freedgo.com 2.亿图（体验了一下，还可） https://www.edrawsoft.cn/edrawmax/

二、常用部分UML使用说明

1.类图：用于描述类及类与类之间的关系。它是从静态的角度对系统进行描述。

1.1 基本类

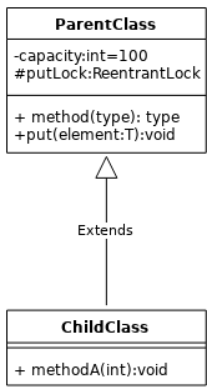
                             （图1）

UML使用矩形框来表示类，矩形框的第一个方框中的文字表示类名，类名上方用书名号括起来的文字为立体型（如图3），它是用来对相应的类做出说明。

矩形的第二个方格表示类的属性列表，这个方格往往只是列出相应的类关键属性，而非全部属性。属性格式为：【属性的可见性】属性名【：属性值类型】【=属性的初始值】。

第二个方格文字前的“+ - #”表示的意义如下表：

                                                   （图2）

类的第三个方格表示类的方法列表。这个方格往往只列出类的关键方法而非全部方法。格式： 【方法的可见性】方法名（【参数列表】）【：返回值类型】

图1中，put方法参数类型是element 具体参数 T 返回值类型void，+ 表示public任意位置可访问。

方法名使用斜体表示，说明相应的方法为抽象方法。方法的可见性及其表示符合如图3所示。

 

1.2类与类之间的关系，包括泛化、实现、关联、依赖、组合和聚集。

泛化关系 表示类（接口）与类（接口）之间的集成关系，即一个类是另外一个类的子类，相当于extends予以。泛化用实线空三角箭头表示。如图1 ChildClass继承ParentClass类

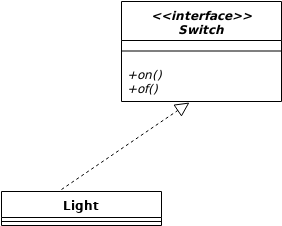
                              （图3）

实现关系 表示某个类继承自那些接口，用虚线空心箭头表示。如图3 Light类继承Switch接口，一个开关控制灯的多种状态，Light是Switch的一种实现。+代表public

说明：在UML图中，箭头是从子类指向父类。大家可以这么理解：定义子类时，要用extends指向父类，所以子类一定知道父类是谁，但是父类不一定知道子类在哪，所以从子类指向父类。

在UML图中：所有抽象类与方法以斜体表示，所有static字段名称加下划线表示。

 

关联关系 一个类拥有某一属性，该属性的类型为另一个类，那么这两个类之间的关系即为关联关系。关联关系从代码的层次理解为一个类拥有一个实例变量，该变量的类型为另一个类。UML中类与类之间的关联关系用实线连接表示。如下图：

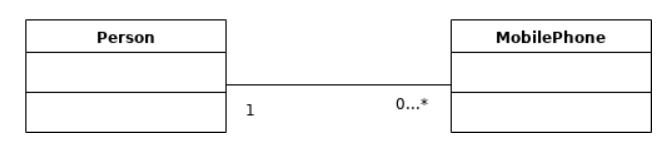
                                  （图4）

表示类与类之间的关联关系的连接线的两端可以带有数字，用于表示数量关系。连接线的两端还可以带有箭头。箭头表示可导航性，即通过一个类可以访问到另外一个类的可能性。存在关联的两个类之间的可导航性可以是双向的也可以是单向的。就上图而言，连接线两端都没有箭头可以理解为双向导航，这种课导航性意味着对于一个人我们可以知道他有多少部手机，对于一个手机我们可以知道它的主人是谁。

0..*表示任意个。

聚集关系它是一种更加具体的关系，表示“有一个（has a）”的关系。在UML中，聚集关系使用一段带宝石符号的连接线来表示。例如，大学里一个系拥有若干教师，这里系与教师之间的关联关系可以用下图表示：

 

组合关系 是一种特殊的聚集关系，有类似数据库的外键特性。在UML中，组合关系使用带实心宝石符号的箭头表示。它与聚集关系的区别具有这种关系的类的实例的生命周期的差别。聚集关系中，一个类的销毁不影响另一个类实例的存在。例如大学里一个系如果不存在了并不影响这个系拥有教师的存在情况（比如可以去其他系任教）。而组合关系定义，一个类的实例的消亡会导致与该类有组合关系的实例的消亡。例如，一个文件夹的删除意味着这个文件夹系下所有的文件也被删除了。如下图：

 

依赖关系 这是一种比较宽松的关系。通常用来表示类与类之间除上述（泛化、实现、关联）关系之外的关系。在UML中，依赖关系使用带箭头的虚线表示。如下图：

展示了木马生成器与密码之间的依赖关系。这里，类PasswordGenerator的newPassword方法会使用到类Password

 

 

2.顺序图

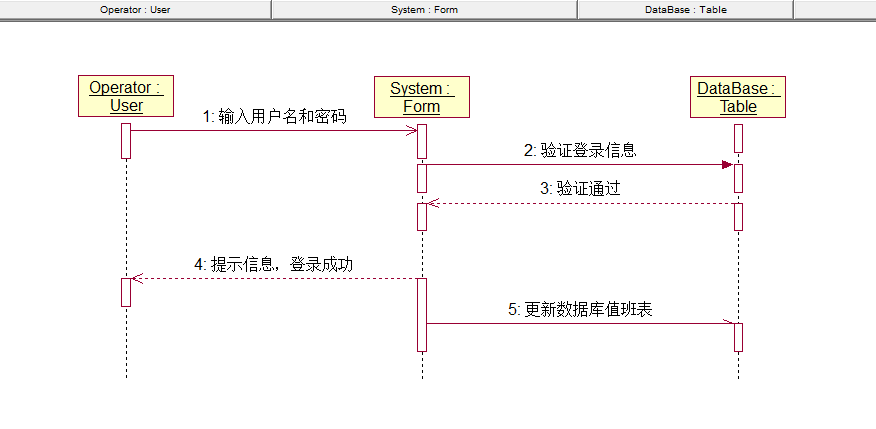
UML的顺序图是用来表示启动程序时，会按照怎样的顺序执行那些方法、那些现象会依什么顺序发生。类图表示“不因时间变化的部分（静态关系），二顺序图则表示”随时间变化的部分（动态行为）“。如下图：

 

上图出现了3个对象实例，分别对应为3个方框。在方框中，类名称写在冒号（：）后面，而且加上下划线，如：Client，意思是Client类的对象实例。如果需要命名，则必须写在冒号之前如server：Server。

所有对象实例都有一条往下延伸的虚线，称为lifeline，所有时间顺序为从上而下，上面是过去，下面是未来。

lifeline中间有一个长方形方框，表示该对象正在操作中。

我们关注到标识为open的箭头，若线段为实线且箭头全黑表示调用方法。因为依成功调用出open方法，所以server对象实例是操作中状态。

open箭头下方虚线箭头表示返回方法，为open的return，可以省略。

因为控制又回到client，所以server对象实例操作中的长方条方框就要结束。继续以同样的方式调用print方法。直接在配套方法内调用device对象实例的write方法。

顺序图自上而下解读，出现箭头时要去确认实例间的协调操作。

 

先写这些，自认为描述的很清楚，所以没写代码。