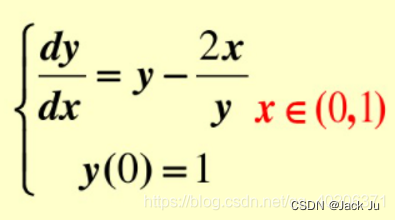一、前言

之前在博客发布了关于使用四阶龙格库塔方法求解一次常微分方程组的文章，由于代码缺少具体的验证，部分朋友可能存在疑问，因此这里打算再重新写一篇博客来验证一下程序的正确性，另外，这里是使用python语言来实现的。

二、RK4求解方程组的要点

使用RK4求解一元方程的过程是非常容易的，但是当转变成多变量的情况下，如何求解方程组，可能有部分朋友会出现问题，这里我总结出来主要有以下要点。

1. 将方程组转化为RK4求解要求的标准形式

RK4求解要求方程具有形如 $\dot{y}=f(y,t)$ 的形式，即是在方程的左边只有变量的一阶微分项，方程的右边包含变量项和自变量项，对于n元情况，我们需要有n个方程，每个方程对应一个自变量项，形式如下：
$\begin{cases} \dot{y_1}=f_1(y_1, \cdots, y_n, t)\\ \quad \quad \vdots \\ \dot{y_n}=f_n(y_1, \cdots, y_n, t)\\ \end{cases}$
转化为标准形式之后就可以进行求解了。

2. 注意区分每个方程的独立性

RK4求解是通过指定一个较小的步进距离，来逐步求解前进一步之后的函数值，每一步下的函数值求解都需要用到前一步的结果，属于递推过程。对于方程组的求解过程，独立性是指针对某个特定变量时，递推公式中只改变特定变量的递推关系，而其它变量不变，例如，方程组中 $y_i$ 的第m+1项的RK4递推关系可以写作：
$\begin{cases} h_m = t_{m+1}-t_m \\ k_{1i}^{m} = f_i(y_1^m, \cdots, y_i^m,\cdots, y_n^m, t_m)\\ k_{2i}^{m} = f_i(y_1^m, \cdots,y_i^m+\frac{h_m}{2}k_{1i}^m,\cdots,y_n^m, t_m+\frac{h_m}{2})\\ k_{3i}^{m} = f_i(y_1^m,\cdots,y_i^m+\frac{h_m}{2}k_{2i}^m,\cdots,y_n^m,t_m+\frac{h_m}{2})\\ k_{4i}^{m} = f_i(y_1^m,\cdots,y_i^m+h_mk_{3i}^m,\cdots,y_n^m,t_m+h_m)\\ y_i^{m+1} = y_i^m+\frac{h_m}{6}(k_{1i}^m+2k_{2i}^m+2k_{3i}^m+k_{4i}^m) \end{cases}$
可以看到在RK4关键变量 $k_1,k_2,k_3,k_4$ 的求解过程中，表达式右边只有第 $y_i$ 项对应的部分代入的值有变化，其它 $y_*$ 项代入的都是上一步（第m步）的计算结果。

三、python实现RK4求解一次常微分方程组

1. 使用的方程组

这里使用的方程组如下图所示：
equations
可以看到该问题存在解析解，解析解留作验证结果准确性。

2. python代码

实现过程中主要使用了numpy库和matplotlib库，以下为代码：

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inlinedef funcXt(x, y):return x + 2.0*ydef funcYt(x, y):return 3.0*x + 2.0*y### RK4求解
t_ini = 0                     # tmin
t_end = 10.0                  # tmax
t_h = 1e-5                    # 步进长度t = np.linspace(t_ini, t_end, int((t_end-t_ini)/t_h+1))
x = t.copy()
y = t.copy()
x[0] = 6.0
y[0] = 4.0
for i in range(t.shape[0]-1):h_i = t[i+1] - t[i]k1_x = funcXt(x[i], y[i])k1_y = funcYt(x[i], y[i])k2_x = funcXt(x[i]+h_i/2.0*k1_x, y[i])k2_y = funcYt(x[i], y[i]+h_i/2.0*k1_y)k3_x = funcXt(x[i]+h_i/2.0*k2_x, y[i])k3_y = funcYt(x[i], y[i]+h_i/2.0*k2_y)k4_x = funcXt(x[i]+h_i*k3_x, y[i])k4_y = funcYt(x[i], y[i]+h_i*k3_y)x[i+1] = x[i] + h_i/6.0*(k1_x+2.0*k2_x+2.0*k3_x+k4_x)y[i+1] = y[i] + h_i/6.0*(k1_y+2.0*k2_y+2.0*k3_y+k4_y)### 解析函数
x_anly = 4.0*np.exp(4.0*t) + 2.0*np.exp(-1.0*t)
y_anly = 6.0*np.exp(4.0*t) - 2.0*np.exp(-1.0*t)### 画图
plt.subplot(1, 2, 1)
plt.plot(t, x, 'b', label='RK4')
plt.plot(t, x_anly, 'r--', label='Analytic')
plt.legend()
plt.xlabel('t')
plt.ylabel('x')
plt.title('x-t')plt.subplot(1, 2, 2)
plt.plot(t, y, 'b', label='RK4')
plt.plot(t, y_anly, 'r--', label='Analytic')
plt.legend()
plt.xlabel('t')
plt.ylabel('y')
plt.title('y-t')# ### 相对误差
# plt.subplot(1, 2, 1)
# plt.scatter(t, (x-x_anly)/x_anly, s=3, label=r'$\frac{x-x_{anly}}{x_{anly}}$')
# plt.legend()
# plt.xlabel('t')
# plt.ylabel('error')
# plt.title('x error')# plt.subplot(1, 2, 2)
# plt.scatter(t, (y-y_anly)/y_anly, s=3, label=r'$\frac{y-y_{anly}}{y_{anly}}$')
# plt.legend()
# plt.xlabel('t')
# plt.ylabel('error')
# plt.title('y error')

3. 运行结果

运行结果为：
output
output1
以上分别是t在0-10和0-1区间上的运行结果，可以看到RK4的计算精度较高，与理论结果较为接近，另外可以看下在0-1区间上RK4的结果相较于理论结果的相对误差：
error
可以看到随着运行步数的增加，RK4计算结果的误差会出现累积，但总体保持在一个相对很低的水平，误差累积的速度较慢。