实验目的

(1) 理解时序图的基本概念；             (2) 理解协作图的基本概念；

(3) 掌握在Rational Rose中绘制交互图的操作方法。

实验内容

一、概要描述交互场景(存款用例)。(文件名命名为存取款交互概要.mdl)

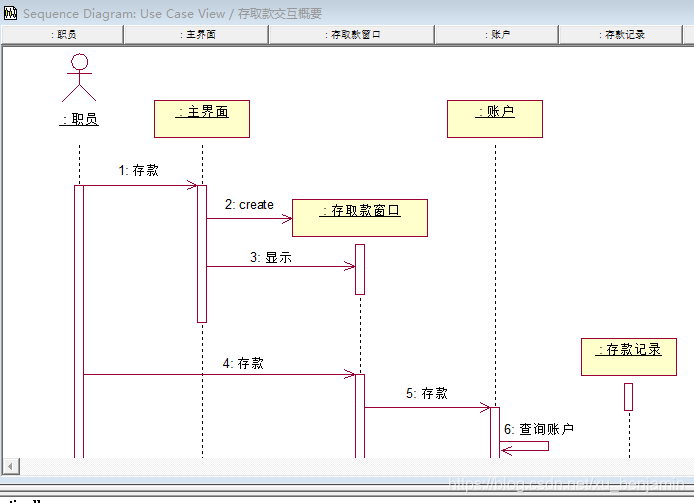
二、设计和绘制自动车锁系统类图；根据类图设计和绘制实现“锁车”用例的顺序图；在顺序图中按【F5】或选择【Browse】à【Creat Collaboration Diagram】自动生成协作图(文件名命名为CarKey.mdl)

三、饮料销售机主要功能如下：

前端(Front)主要功能：1.接受顾客的选购和现钞  2.从记录器接收找回的零钱并交给顾客  3.返还现钞  4.从分配器接收饮料   5.显示信息

记录器(Register)：1.从前端获取顾客输入  2.更新现钞存储  3.找零钱

分配器(Dispenser)：1.检查顾客选购的饮料是否有货  2. 分发饮料

1. 设计和绘制饮料销售机类图；2. 根据类图和最理想场景、sold-out场景、没有使用合适现金--找零钱场景、没有使用合适零钱--找不开场景顺序图设计和绘制饮料销售机完整顺序图；(文件名命名为SodaMachine.mdl)

    最理想场景--顺序图：

sold-out场景--顺序图：

    没有使用合适现金--找零钱场景--顺序图：

没有使用合适零钱--找不开场景--顺序图：