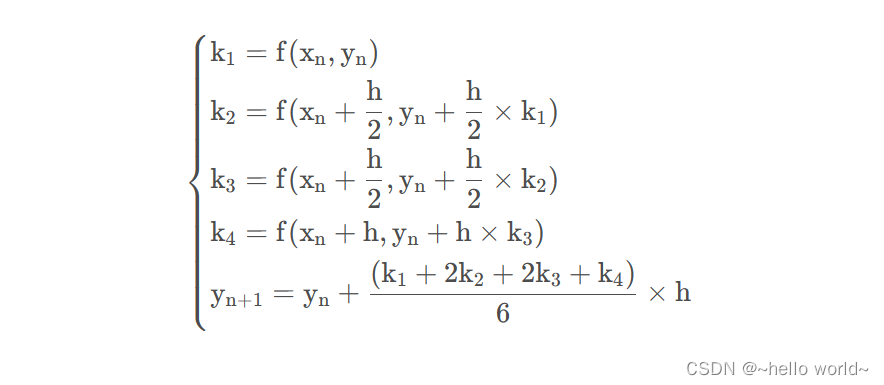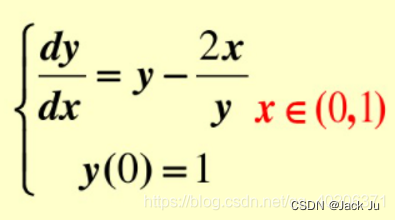隐式龙格-库塔法
- 题目
- 具体分析
- 前期准备
- 确定系数
- MATLAB求解
题目
用隐式中点公式求解常微分方程:
{ d y d x = y , y ( 0 ) = 1. \begin{cases} \dfrac{dy}{dx}=y,\\ y(0)=1. \end{cases} ⎩⎨⎧dxdy=y,y(0)=1.
具体分析
前期准备
首先对和在区间上进行离散化,然后构造递推公式,再进一步得到在这些位置的近似取值。
这些离散位置可以表示为:
x 1 , x 2 , ⋯ , x n , ⋯ x_{1},x_{2},\cdots,x_{n},\cdots x1,x2,⋯,xn,⋯
显然, y ( x ) y(x) y(x)在这些离散的点处精确取值为:
y ( x 1 ) , y ( x 2 ) , ⋯ , y ( x n ) , ⋯ y(x_1),y(x_2),\cdots,y(x_n),\cdots y(x1),y(x2),⋯,y(xn),⋯
令相邻两个离散点的间隔为一定值 h h h,则有 x n = x 1 + n h ( n = 1 , 2 , ⋯ ) x_n=x_1+nh(n=1,2,\cdots) xn=x1+nh(n=1,2,⋯),记 f ( x , y ) = y f(x,y)=y f(x,y)=y。
p级隐式R-K方法(类似于龙格-库塔法的思想)
{ y n + 1 = y n + h ∑ r = 1 p λ r K r , K r = f ( x n + α r h , y n + h ∑ i = 1 p λ r i K i ) , r = 1 , 2 , ⋯ , p . \begin{cases} y_{n+1}=y_{n}+h\sum\limits_{r=1}^{p}\lambda_{r}K_{r},\\ K_{r}=f(x_n+\alpha_{r}h,y_{n}+h\sum\limits_{i=1}^{p}\lambda_{ri}K_{i}),r=1,2,\cdots,p.\\ \end{cases} ⎩⎪⎪⎨⎪⎪⎧yn+1=yn+hr=1∑pλrKr,Kr=f(xn+αrh,yn+hi=1∑pλriKi),r=1,2,⋯,p.
我们可利用 T a y l o r Taylor Taylor展开确定系数。(下面以r=1为例)
确定系数
{ y n + 1 = y n + h λ K , ( 1 ) K = f ( x n + α h , y n + h λ ∗ K ) . ( 2 ) \begin{cases} y_{n+1}=y_{n}+h\lambda K,&(1)\\ K=f(x_n+\alpha h,y_{n}+h\lambda_{*}K).&(2)\\ \end{cases} {yn+1=yn+hλK,K=f(xn+αh,yn+hλ∗K).(1)(2)
首先,我们对二式中对 f f f在 x n x_n xn出 T a y l o r Taylor Taylor展开,得:
K = f ( x n , y n ) + f x ( x n , y n ) α h + f y ( x n , y n ) h λ ∗ K + o ( h 2 ) K=f(x_n,y_n)+f_x(x_n,y_n)\alpha h+f_y(x_n,y_n)h\lambda_{*}K+o(h^2) K=f(xn,yn)+fx(xn,yn)αh+fy(xn,yn)hλ∗K+o(h2)
解出 K = f ( x n , y n ) + f x ( x n , y n ) α h 1 − f y ( x n , y n ) h λ ∗ K=\frac{f(x_n,y_n)+f_x(x_n,y_n)\alpha h}{1-f_y(x_n,y_n)h\lambda_{*}} K=1−fy(xn,yn)hλ∗f(xn,yn)+fx(xn,yn)αh,
代入(1)式得:
y n + 1 = y n + h λ f ( x n , y n ) + f x ( x n , y n ) α h 1 − f y ( x n , y n ) h λ ∗ y_{n+1}=y_{n}+h\lambda\frac{f(x_n,y_n)+f_x(x_n,y_n)\alpha h}{1-f_y(x_n,y_n)h\lambda_{*}} yn+1=yn+hλ1−fy(xn,yn)hλ∗f(xn,yn)+fx(xn,yn)αh
与 y ( x n + 1 ) y(x_{n+1}) y(xn+1)在 x n x_n xn处 T a y l o r Taylor Taylor展开进行比较:
y ( x n + 1 ) = y ( x n ) + h 1 ! y ′ ( x n ) + h 2 2 ! y ′ ′ ( x n ) + ⋯ y(x_{n+1})=y(x_n)+\frac{h}{1!}y^{'}(x_n)+\frac{h^2}{2!}y^{''}(x_n)+\cdots y(xn+1)=y(xn)+1!hy′(xn)+2!h2y′′(xn)+⋯
得到:
h λ f ( x n , y n ) + f x ( x n , y n ) α h 1 − f y ( x n , y n ) h λ ∗ ≈ h 1 ! y ′ ( x n ) + h 2 2 ! y ′ ′ ( x n ) h\lambda\frac{f(x_n,y_n)+f_x(x_n,y_n)\alpha h}{1-f_y(x_n,y_n)h\lambda_{*}}\approx\frac{h}{1!}y^{'}(x_n)+\frac{h^2}{2!}y^{''}(x_n) hλ1−fy(xn,yn)hλ∗f(xn,yn)+fx(xn,yn)αh≈1!hy′(xn)+2!h2y′′(xn)
即:
λ f ( x n , y n ) + f x ( x n , y n ) α h 1 − f y ( x n , y n ) h λ ∗ ≈ f ( x n , y n ) + h 2 [ f x ( x n , y n ) + f y ( x n , y n ) f ( x n , y n ) ] \lambda\frac{f(x_n,y_n)+f_x(x_n,y_n)\alpha h}{1-f_y(x_n,y_n)h\lambda_{*}}\approx f(x_n,y_n)+\frac{h}{2}[f_x(x_n,y_n)+f_y(x_n,y_n)f(x_n,y_n)] λ1−fy(xn,yn)hλ∗f(xn,yn)+fx(xn,yn)αh≈f(xn,yn)+2h[fx(xn,yn)+fy(xn,yn)f(xn,yn)]
简记为:
λ f + f x α h 1 − f y h λ ∗ ≈ f + h 2 ( f x + f y f ) \lambda\frac{f+f_x\alpha h}{1-f_y h\lambda_{*}}\approx f+\frac{h}{2}(f_x+f_y f) λ1−fyhλ∗f+fxαh≈f+2h(fx+fyf)
化简得:
λ f + λ f x α h = f − f f y h λ ∗ + 1 2 h f x + 1 2 h f y f \lambda f+\lambda f_x\alpha h=f-ff_y h \lambda_{*}+\frac{1}{2}h f_x+\frac{1}{2}h f_y f λf+λfxαh=f−ffyhλ∗+21hfx+21hfyf
解得:
λ = 1 , λ ∗ = 1 2 , α = 1 2 . \lambda=1,\lambda_{*}=\frac{1}{2},\alpha=\frac{1}{2}. λ=1,λ∗=21,α=21.
从而得到隐式中点公式:
{ y n + 1 = y n + h K , ( 1 ) K = f ( x n + 1 2 h , y n + 1 2 h K ) . ( 2 ) \begin{cases} y_{n+1}=y_{n}+h K,&(1)\\ K=f(x_n+\frac{1}{2} h,y_{n}+\frac{1}{2}h K).&(2)\\ \end{cases} {yn+1=yn+hK,K=f(xn+21h,yn+21hK).(1)(2)
MATLAB求解
% Implicit kutta
clear all,close all,clc
f=@(x,y)y;
N=10;h=1/N;
x=linspace(0,1,N+1);
y=[1,zeros(1,N)];
K=randn(1);
for n=1:NK=f(x(n)+1/2*h,y(n)+1/2*h*K);y(n+1)=y(n)+h*K;
end
y_exact=@(x)exp(x);
plot(x,y_exact(x),'-b',x,y,'*r')
axis([0 1 0.9 3.5]),xlabel x,ylabel y
legend('Exact','ImKutta')
error=y_exact(x)-y;