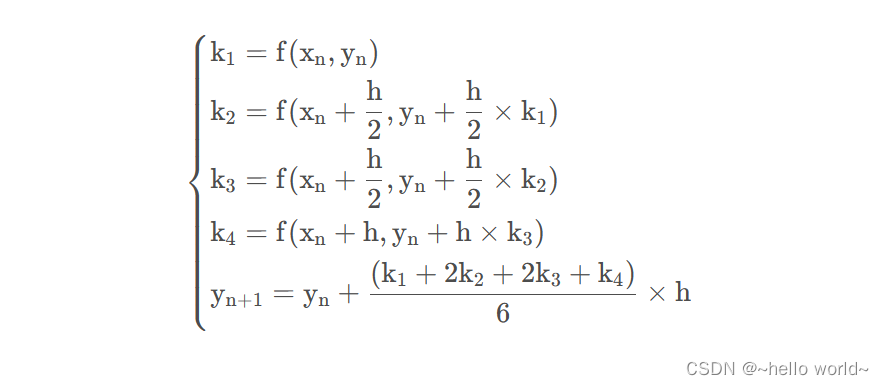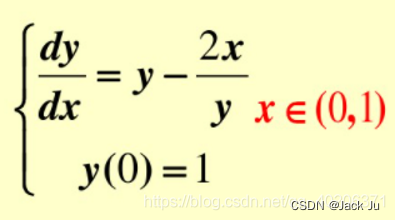简介

通过求解简单的初值问题：
$$\{\begin{array}{llccccc}\frac{du}{dx}=f(x,u)& & & & & & (1)\\ u(x_0)=u_0& & & & & & (2)\end{array}$$
引入欧拉法、改进的欧拉法、龙格-库塔法等。

前期准备

数值解法的基本思想就是先对$x$和$u(x)$在区间$[x_0,\infty )$上进行离散化，然后构造递推公式，再进一步得到$u(x)$在这些位置的近似取值。

• 取定步长$h$，令$x_n=x_0+nh(n=\pm 1,\pm 2,\cdots )$
• 得到离散的位置：$x_1,x_2,\cdots ,x_n,\cdots$
• $u(x)$在这些点精确取值为：$u(x_1),u(x_2),\cdots ,u(x_n),\cdots$
• 利用数值解法得到的这些点的近似取值，记为$u_1,u_2,\cdots ,u_n,\cdots$

欧拉法

欧拉法的核心就是将导数近似为差商。
将导数近似为向前差商，则有：
$${\frac{du}{dx}|}_{x=x_n}\approx \frac{u(x_{n+1})-u(x_n)}{h}$$
代入(1)式，有：
$$u(x_{n+1})=y(x_n)+hf(x_n,u(x_n))$$
用$u_{n+1}$和$u_n$代替$u(x_{n+1})$和$u(x_n)$，得：
$$u_{n+1}=u_n+hf(x_n,u_n)$$
因此，若知道$u_0$我们就可以递归出$u_1,u_2,\cdots$
如果将导数近似为向后差商:
$${\frac{du}{dx}|}_{x=x_n}\approx \frac{u(x_n)-u(x_{n-1})}{h}$$
类似的，就可以得到：
$$u_{n-1}=u_n-hf(x_n,u_n)$$
这样，若知道$u_0$我们就可以递归出$u_{-1},u_{-2},\cdots$

改进的欧拉法

对$(1)$式在$[x_n,x_{n+1}]$上积分，可得：
$$u(x_{n+1})=u(x_n)+{\int }_{x_n}^{x_{n+1}}f(x,u)dx$$
其中，$n=0,1,\cdots$。用不同方式来近似上式的积分运算，就会得到不同的递推公式。若使用左端点计算矩形面积并取近似：
$${\int }_{x_n}^{x_{n+1}}f(x,u)dx\approx hf(x_{n+1},u(x_{n+1}))$$
代入上式得：
$$u_{n+1}=u_n+hf(x_n,u_n)$$
若使用梯形的面积做近似：
$${\int }_{x_n}^{x_{n+1}}f(x,y)dx\approx \frac{h}{2}[f(x_n,u(x_n))+f(x_{n+1},u(x_{n+1}))]$$
得到：
$$u_{n+1}=u_n+\frac{h}{2}[f(x_n,u_n)+f(x_{n+1},u_{n+1})]$$
欧拉法虽然精度偏低，但它是显式的，可直接得到结果。而梯形公式是隐式的，虽然精度较高，却无法通过一步计算得到结果，若用迭代法计算，运算量较大。综合这两种方法，可以相得益彰：先用显式格式却低精度的欧拉法计算得到一个粗略的预测值${\bar{u}}_{n+1}$，再将这个预测值代入梯形公式进行修正，得到较高精度的结果$u_{n+1}$。
$$\{\begin{array}{l}{\bar{u}}_{n+1}=u_n+hf(x_n,u_n)\\ u_{n+1}=u_n+\frac{h}{2}[f(x_n,u_n)+f(x_{n+1},{\bar{u}}_{n+1})]\end{array}$$

龙格-库塔法

将以上两种方法分别写成如下形式：
$$\{\begin{array}{l}{u}_{n+1}=u_n+h{K}_1\\ K_1=f(x_n,u_n)\end{array}$$
$$\{\begin{array}{l}{u}_{n+1}=u_n+\frac{h}{2}(K_1+K_2)\\ K_1=f(x_n,u_n)\\ K_2=f(x_n+h,u_n+K_1)\end{array}$$
上述方法都是通过$f(x,u)$在不同位置的线性组合来计算$u_{n+1}$的值，所考虑的位置越多，精度也越高。类似的，就得到龙格-库塔法的思想：如果用$f(x,u)$在更多位置的线性组合来构造递推公式，将会得到更高的精度。
这样，递推公式将有如下形式：
$$\{\begin{array}{l}{u}_{n+1}=u_n+h\sum _{i=1}^r{R}_i{K}_i\\ K_1=f(x_n,u_n)\\ K_i=f(x_n+a_{i}h,u_n+\sum _{j=1}^{i-1}{b}_{ij}{K}_j),i=2,3,\cdots ,r\end{array}$$
其中，$R_i,a_i,b_{ij}$为待定常数。(利用$Taylor$展开就可以确定待定系数)

标准四阶显式Kutta公式

$$\{\begin{array}{l}{y}_{n+1}=y_n+\frac{h}{6}(K_1+4K_2+K_3),\\ K_1=f(x_n,y_n),\\ K_2=f(x_n+\frac{1}{2}h,y_n+\frac{1}{2}h{K}_1),\\ K_3=f(x_n+h,y_n-h{K}_1+2h{K}_2);\end{array}$$

三级三阶显式公式

$$\{\begin{array}{l}{y}_{n+1}=y_n+\frac{h}{4}(K_1+3K_3),\\ K_1=f(x_n,y_n),\\ K_2=f(x_n+\frac{1}{3}h,y_n+\frac{1}{3}h{K}_1),\\ K_3=f(x_n+\frac{2}{3}h,y_n+\frac{2}{3}h{K}_2);\end{array}$$

四级四阶显式Kutta公式

$$\{\begin{array}{l}{y}_{n+1}=y_n+\frac{h}{8}(K_1+3K_2+3K_3+K_4),\\ K_1=f(x_n,y_n),\\ K_2=f(x_n+\frac{1}{3}h,y_n+\frac{1}{3}h{K}_1),\\ K_3=f(x_n+\frac{2}{3}h,y_n-\frac{2}{3}h{K}_1+h{K}_2),\\ K_4=f(x_n+h,y_n+h{K}_1-h{K}_2+h{K}_3);\end{array}$$

四级四阶显式Gill公式

$$\{\begin{array}{l}{y}_{n+1}=y_n+\frac{h}{6}(K_1+(2-\sqrt{2})K_2+(2+\sqrt{2})K_3+K_4),\\ K_1=f(x_n,y_n),\\ K_2=f(x_n+\frac{1}{2}h,y_n+\frac{1}{2}h{K}_1),\\ K_3=f(x_n+\frac{1}{2}h,y_n+\frac{\sqrt{2}-1}{2}h{K}_1+(1-\frac{\sqrt{2}}{2})h{K}_2),\\ K_4=f(x_n+h,y_n-\frac{\sqrt{2}}{2}h{K}_2+(1+\frac{\sqrt{2}}{2})h{K}_3);\end{array}$$

示例

求解常微分方程:
$$\{\begin{array}{l}\frac{dy}{dx}=x^3-\frac{y}{x},\\ y(1)=\frac{2}{5}.\end{array}$$
要求步长为$h=0.1$，其中，精确解为
$$y=\frac{1}{5}{x}^4+\frac{1}{5x}.$$

MATLAB代码

clear all,close all,clc
f=@(x,y)x^3-y/x;
h=0.1;
%% Euler method
x=[1:h:2];
N=size(x,2)-1;
y1=[2/5,zeros(1,N)];
for n=1:Ny1(n+1)=y1(n)+h*f(x(n),y1(n));
end
%% Improved Euler method
y2=[2/5,zeros(1,N)];
for n=1:Ny2(n+1)=y2(n)+h*f(x(n),y2(n));y2(n+1)=y2(n)+h/2*(f(x(n),y2(n))+f(x(n+1),y2(n+1)));
end
%% Standard fourth-order explicit Kutta formula
y3=[2/5,zeros(1,N)];
for n=1:NK1=f(x(n),y3(n));K2=f(x(n)+1/2*h,y3(n)+1/2*h*K1);K3=f(x(n)+h,y3(n)-h*K1+2*h*K2);y3(n+1)=y3(n)+h/6*(K1+4*K2+K3);
end
%% Three-level three-order explicit formula
y4=[2/5,zeros(1,N)];
for n=1:NK1=f(x(n),y4(n));K2=f(x(n)+1/3*h,y4(n)+1/3*h*K1);K3=f(x(n)+2/3*h,y4(n)+2/3*h*K2);y4(n+1)=y4(n)+h/4*(K1+3*K3);
end
%% Fourth-level fourth-order explicit Kutta formula
y5=[2/5,zeros(1,N)];
for n=1:NK1=f(x(n),y5(n));K2=f(x(n)+1/3*h,y5(n)+1/3*h*K1);K3=f(x(n)+2/3*h,y5(n)-1/3*h*K1+h*K2);K4=f(x(n)+h,y5(n)+h*K1-h*K2+h*K3);y5(n+1)=y5(n)+h/8*(K1+3*K2+3*K3+K4);
end
%% Fourth-level fourth-order explicit Gill formula
y6=[2/5,zeros(1,N)];
for n=1:NK1=f(x(n),y6(n));K2=f(x(n)+1/2*h,y6(n)+1/2*h*K1);K3=f(x(n)+1/2*h,y6(n)+(sqrt(2)/2-0.5)*h*K1+(1-sqrt(2)/2)*h*K2);K4=f(x(n)+h,y6(n)-sqrt(2)/2*h*K2+(1+sqrt(2)/2)*h*K3);y6(n+1)=y6(n)+h/6*(K1+(2-sqrt(2))*K2+(2+sqrt(2))*K3+K4);
end
y=1/5*x.^4+1./(5*x);  %  Exact solutionplot(x,y,'k',x,y1,'xr',x,y2,'ob','Markersize',10,'LineWidth',1.5)
axis([1 2.1 0 4.5]),xlabel x,ylabel u
legend('Exact','Euler','Improved Euler')%plot(x,y,'k',x,y3,'*r',x,y4,'+b',x,y5,'-y',x,y6,'or','Markersize',10,'LineWidth',1.5)
%axis([1 2.1 0 6]),xlabel x,ylabel u,set(gca,'Fontsize',18)
%legend('Exact','34Kutta','33kutta','44Kutta','44Gill')

结果