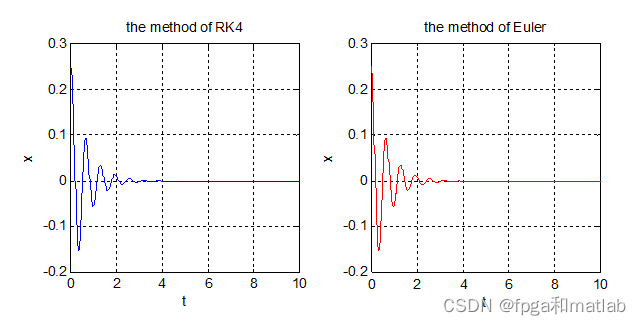
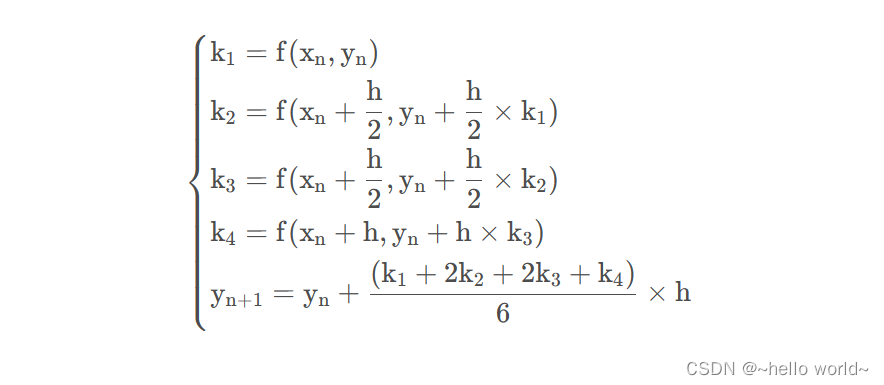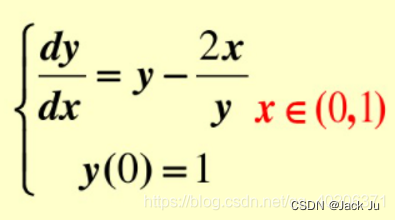相关文章
Matlab 四阶龙格库塔法求解二元常微分方程组
龙格库塔法是一种求解高阶常微分方程的常用方法,在工程当中应用广泛,例如求解物体的运动方程等。 这里我们通过matlab程序编写龙格库塔算法求解二元常微分方程组,假设有常微分方程组: { x − x ˙ 2 y y ˙ − 2 s i n t −…
四阶龙格库塔法求解微分方程【MATLAB||C】
四阶龙格库塔法求解微分方程 作者:PEZHANG 时间:2021.11.6 求解过程数学描述
四阶龙格库塔的求解过程可用如下数学公式描述: k 1 f ( t n , y n ) k_1f\left( t_n,y_n \right) k1f(tn,yn) k 2 f ( t n h 2 , y n h 2 k 1 ) k_2f\…
算法-----龙格-库塔法(转)
数值分析中,龙格-库塔法(Runge-Kutta)是用于模拟常微分方程的解的重要的一类隐式或显式迭代法。这些技术由数学家卡尔龙格和马丁威尔海姆库塔于1900年左右发明。 龙格库塔法的家族中的一个成员如此常用,以至于经常被称…
隐式龙格库塔法举例说明
隐式龙格-库塔法 题目具体分析前期准备确定系数MATLAB求解 题目
用隐式中点公式求解常微分方程: { d y d x y , y ( 0 ) 1. \begin{cases} \dfrac{dy}{dx}y,\\ y(0)1. \end{cases} ⎩⎨⎧dxdyy,y(0)1.
具体分析
前期准备
首先对和在区间上进行离散化,然…
龙格库塔法求解微分方程
在https://blog.csdn.net/weixin_42141390/article/details/110184743一文中,我们曾经讨论了欧拉法,龙格-库塔法也跟欧拉法一样,是用梯形的面积去替代积分的面积的一种方法。
欧拉法简介
设有微分方程: d x ( t ) d t f ( x )…
数值计算大作业:常微分初值问题数值解法(欧拉法、改进欧拉法、四阶龙格库塔法程序在Matlab中的实现)
作为研究生的入门课,数值计算的大作业算是所有研究生开学的重要编程作业。 我把矩常微分初值问题用欧拉法、改进欧拉法、与四阶龙格库塔法分别在MATLAB中编程实现。具体的程序详细标注后放在文章最后了,每道题我只展示运算结果与结论,需要的同…
Matlab之四阶龙格—库塔法方法:解常微分初值问题
目录
1. 题目
2. 算法原理
3. 代码
4. 结果
4.1 运行结果
4.2 结果分析 【若觉文章质量良好且有用,请别忘了点赞收藏加关注,这将是我继续分享的动力,万分感谢!】
直接通过解题的方式进行学习,代入感更强
1. 题…
龙格库塔方法的原理和案例及MTATLAB编程
文章目录 龙格库塔法的原理利用四阶龙格库塔法求解一个案例用MATLAB编程 龙格库塔法的原理 在百度百科中是这么解释的:在各种龙格-库塔法当中有一个方法十分常用,以至于经常被称为“RK4”或者就是“龙格-库塔法”。该方法主要是在…
欧拉法、改进的欧拉法、龙格-库塔法求解初值问题
求解初值问题 简介前期准备欧拉法改进的欧拉法龙格-库塔法标准四阶显式Kutta公式三级三阶显式公式四级四阶显式Kutta公式四级四阶显式Gill公式 示例MATLAB代码结果 简介
通过求解简单的初值问题: { d u d x f ( x , u ) ( 1 ) u ( x 0 ) u 0 ( 2 ) \begin{cases…
6.2 龙格—库塔法
学习目标:
学习龙格-库塔法的具体明确的学习目标可以有以下几点: 理解龙格-库塔法的基本思想和原理:我们应该了解龙格-库塔法的数值求解思想和数值误差的概念,包括截断误差和稳定性等基本概念,并且要熟悉龙格-库塔法的…
四阶龙格库塔法求解一次常微分方程组(python实现)
四阶龙格库塔法求解一次常微分方程组 一、前言二、RK4求解方程组的要点1. 将方程组转化为RK4求解要求的标准形式2. 注意区分每个方程的独立性 三、python实现RK4求解一次常微分方程组1. 使用的方程组2. python代码3. 运行结果 一、前言
之前在博客发布了关于使用四阶龙格库塔方…
四阶龙格库塔算法及matlab代码
常微分方程
Ordinary differential equation,简称ODE,自变量只有一个的微分方程。 例子1: d y d x f ( x , y ) \dfrac {dy} {dx}f(x,y) dxdyf(x,y) , f ( x , y ) f(x,y) f(x,y)是已知函数
偏微分方程
Partial differential equation…
四阶龙格库塔法(Runge-Kutta)求解常微分方程的 Matlab程序及案例
文章目录 1. 算法2. 程序3. 案例4. 联系作者 1. 算法
上一篇介绍了显式欧拉法、隐式欧拉法、两步欧拉法和改进欧拉法求解常微分方程初值问题;其中显式欧拉法和隐式欧拉法是一阶算法精度,截断误差为 O ( h 2 ) O\left( {{h^2}} \right) O(h2);…
【Runge-Kutta】龙格-库塔法求解微分方程matlab仿真
1.软件版本
MATLAB2013b
2.算法理论 龙格-库塔法(Runge-Kutta)是用于模拟常微分方程的解的重要的一类隐式或显式迭代法。龙格库塔法的家族中的一个成员如此常用,以至于经常被称为“RK4”或者就是“龙格库塔法”。令初值问题表述…
龙格-库塔方法学习笔记
1、龙格-库塔法简介 龙格—库塔法是一种在工程上应用广泛的高精度单步算法,其中包括著名的欧拉法,用于数值求解微分方程。 由于此算法精度高,采取措施对误差进行抑制,所以其实现原理也较复杂。 在各种龙格—库塔法当中有一个方法十…
四阶龙格库塔法的计算例子
序
没有对比就没有伤害,本文先给出很多时候直接采用的矩形法,然后与四阶龙格库塔法做比较,着重说明四阶龙格库塔法。 一、矩形法 1.1 原理
设微分方程 y ˙ f ( y ) (1.1) \dot yf(y) \tag{1.1} y˙f(y)(1.1)
求 y y y。
使用数值方法…
龙格-库塔法(Runge-Kutta methods)
非线性的常微分方程通常是难以求出解析解的,只能通过多次迭代求近似的数值解。
龙格-库塔法(Runge-Kutta methods)是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。简写做RK法。
对于任意的Yf(X),假设某点(Xi,Yi)的斜…
龙格-库塔(Runge-Kutta)方法C++实现
龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。由于此算法精度高,采取措施对误差进行抑制,所以其实现原理也较复杂。该算法是构建在数学支持的基础之上的。
1 中点法 2传统二阶龙格库塔法: 3 传统三阶龙格库塔法 4 传…