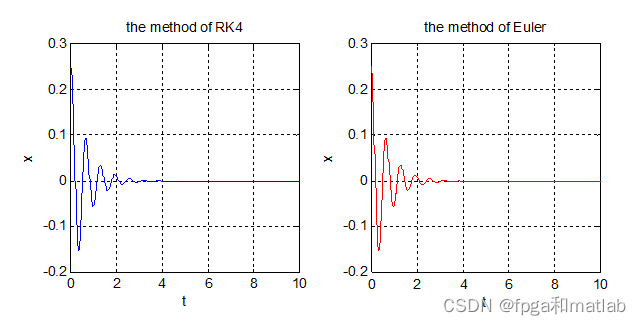
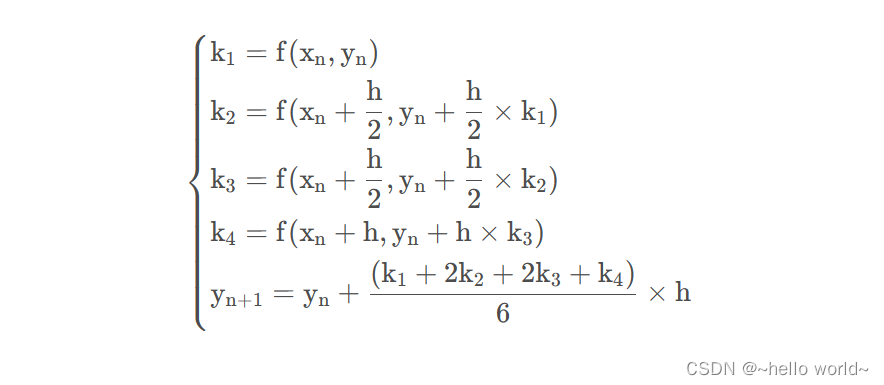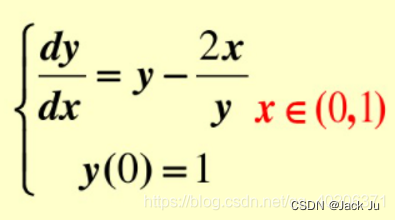在https://blog.csdn.net/weixin_42141390/article/details/110184743一文中，我们曾经讨论了欧拉法，龙格-库塔法也跟欧拉法一样，是用梯形的面积去替代积分的面积的一种方法。

欧拉法简介

设有微分方程：
$$\frac{dx(t)}{dt}=f(x)$$
$x(t_0)=x_0$已知。

我们对上述方程进行积分，积分区域为$[t_0,t_1],\Delta t=t_1-t_0$，可得：
$$x(t_1)=x(t_0)+{\int }_{t_0}^{t_1}f(t)dt$$
其中$x(t_1)$就是我们要求解的东西了。于是，就差积分怎么解决了。

对于欧拉法来说，积分是靠梯形面积来近似，如下所示：
$${\int }_{t_0}^{t_1}f(t)dt=f(x(t_0))(t_1-t_0)=f(x_0)\Delta t$$
带入上述方程即可得：
$$x(t_1)=x(t_0)+f(x_0)\Delta t$$
按照上式进行递推，即可得：
$$x_{k+1}=x_k+f(x_k)\Delta t$$
其中 $x_0$ 已知。问题就搞定了。

二阶龙格-库塔法

对于微分方程 $\frac{dx}{dt}=f(x)$
由于梯形的上底取得不合理，导致欧拉法存在一定的误差和不稳定性，于是需要对其进行改进。龙格库塔法的递推公式为：
$$x_k=x_{k-1}+\Delta t({\lambda }_1{m}_1+{\lambda }_1{m}_2)$$
其中：$m_1=f(x_{k-1})$、$m_2=f(x_{k-1}+m_1\cdot p\Delta t)$，且 $p\cdot {\lambda }_2=1/2,{\lambda }_1+{\lambda }_2=1$

若：$p=1,{\lambda }_1=1/2,{\lambda }_2=1/2$，则二阶龙格-库塔法等价于改进欧拉法。

高阶龙格-库塔法

我们可以对二阶龙格-库塔法进行推广，如三阶龙格-库塔法的递推公式为：
$$x_k=x_{k-1}+\frac{\Delta t}{6}(m_1+4m_2+m_3)$$
其中：$m_1=f(x_{k-1}),m_2=f(x_{k-1}+1/2\cdot m_1\Delta t),m_3=f(x_{k-1}+(2m_2-m1)\Delta t)$

也有四阶龙格库塔法（最常用）：
$$x_k=x_{k-1}+\frac{\Delta t}{6}(m_1+2m_2+2m_3+m_4)$$
其中：$m_1=f(x_{k-1}),m_2=f(x_{k-1}+1/2\cdot m_1\Delta t),m_3=f(x_{k-1}+1/2\cdot m_2\Delta t),m_4=f(x_{k-1}+m_3\Delta t)$

就如我们在欧拉法这篇文章讲的那样，我们可以用泰勒公式来确定龙格库塔法的精确度，可以证明的是，多少阶的龙格库塔法，就有多少阶的精确度。

案例与代码

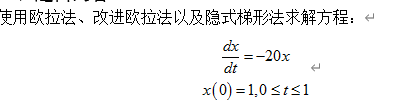
可见求解区域为 [0，1]，我们设置求解的步数为 100，也即 $\Delta t=0.01s$，代码如下：

import numpy as np
import matplotlib.pyplot as plt
def f(x):return -20*x
def lgkt3(n,x0,t0,tn,f):x = [x0]t = [t0]for i in range(n):dt = (tn-t0)/ntk = t[i]+dtt.append(tk)m1 = f(x[i])*dtm2 = f(x[i]+m1*dt/2)m3 = f(x[i]+(2*m2-m1)*dt)xk = x[i]+dt/6*(m1+4*m2+m3)x.append(xk)return x,tdef lgkt4(n,x0,t0,tn,f):x = [x0]t = [t0]for i in range(n):dt = (tn-t0)/ntk = t[i]+dtt.append(tk)m1 = f(x[i])*dtm2 = f(x[i]+m1*dt/2)m3 = f(x[i]+m2*dt/2)m4 = f(x[i]+m3*dt)xk = x[i]+dt/6*(m1+2*m2+2*m3+m4)x.append(xk)return x,t        
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = Falsefont1 = {'family' : 'SimHei',
'weight' : 'normal',
'size'   : 15,
}def myplot2(n,x0,t0,tn,f):x1,t = lgkt3(n,x0,t0,tn,f)x2,t = lgkt4(n,x0,t0,tn,f)plt.figure(figsize=(12,4))plt.subplot(1,2,1)plt.plot(t,x1,linewidth=3,color='r',label='3阶龙格库塔法')    plt.xlabel('t',fontsize=24)plt.ylabel('x',fontsize=24)plt.legend(prop=font1)plt.grid()plt.subplot(1,2,2)plt.plot(t,x2,linewidth=3,color='b',label='4阶龙格库塔法')plt.xlabel('t',fontsize=24)plt.ylabel('x',fontsize=24)plt.legend(prop=font1)plt.grid()if __name__ == '__main__':myplot2(10,1,0,1,f)