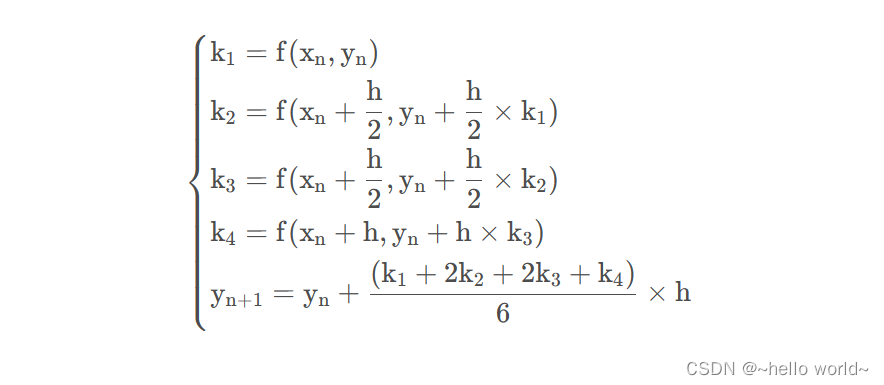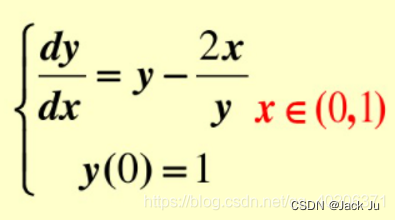经典四阶龙格库塔法

article/2025/8/29 22:17:29

关注微信公众号“二进制小站”获取更多分析（文末二维码~~）

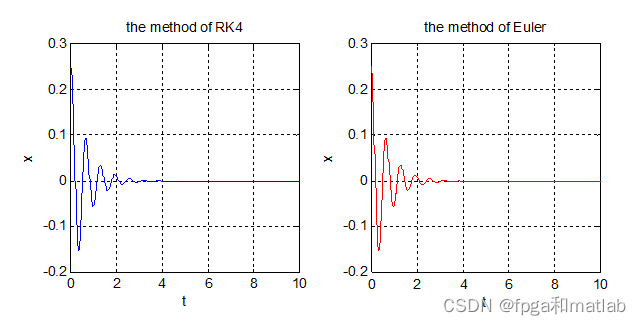
龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法,经常被称为“RK4”或者就是“龙格库塔法”。

令初值问题表述如下。

对于该问题的RK4由如下方程给出：

其中：

RK4法是四阶方法，也就是说每步的误差是h5阶，而总积累误差为h4阶。

RK4计算程序如下：

//visualsan@yahoo.cn
#include <iostream>
using namespace std;#include <vector>
#include <math.h>
using namespace std;
class RK  
{
public:class DiffFunc{public:double operator()(double x,double y){// y'=cos(x)return cos(x);// y'=x*y-1//    return x*y-1;}} m_df;RK(double xend,double x0,double y0,double h=1e-3){m_max_x = xend;m_x0 = x0;m_y0 = y0;m_h = h;m_half_h=h/2.0;}void Solve(){double yn=m_y0,xstart=m_x0;while( xstart<m_max_x){double y=yn+K(xstart,yn)*m_h;//y(n+1)=y(n)+h*y'm_x.push_back(xstart);m_y.push_back(yn);cout<<xstart<<""<<yn<<endl;yn=y;xstart+=m_h;}    }//求解后的点std::vector<double> m_x,m_y;//步长hdouble m_h;//初始点x0,y0double m_x0,m_y0;//x范围double m_max_x;private:double m_half_h;double m_ptx,m_pty;double  K1(double x,double y){double v=m_df(x,y);m_ptx=x;m_pty=y;return v;}double  K2(double _k1){double v=m_df(m_ptx+m_half_h,m_pty+m_half_h*_k1);return v;}double  K3(double _k2){double v=m_df(m_ptx+m_half_h,m_pty+m_half_h*_k2);return v;}double  K4(double _k3){double v=m_df(m_ptx+m_h,m_pty+m_h*_k3);return v;}double  K(double x,double y){double _k1=K1(x,y),_k2=K2(_k1),_k3=K3(_k2),_k4=K4(_k3);return  (_k1+2.0*_k2+2.0*_k3+_k4)/6.0;}};main()
{RK s1(1,0,0);s1.Solve();
}

计算实例：

y'=cos(x) y(0)=0, -> solution y=sin(x)