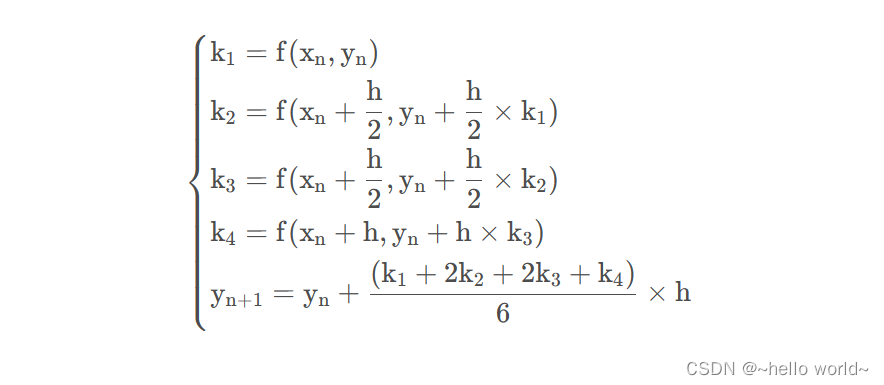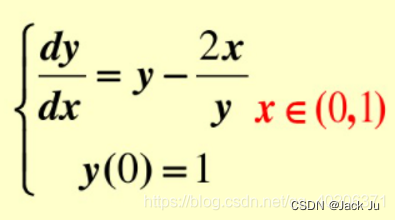作为研究生的入门课，数值计算的大作业算是所有研究生开学的重要编程作业。

    我把矩常微分初值问题用欧拉法、改进欧拉法、与四阶龙格库塔法分别在MATLAB中编程实现。具体的程序详细标注后放在文章最后了，每道题我只展示运算结果与结论，需要的同学自取。下面为作业详解

题目：给定常微分方程初值问题y，=-20*y,0<x≤1;y(0)=1;完成以下工作

1.取h=0.1和h=0.05，使用欧拉法计算，绘制出数值解和精确解图形，观察数值解的稳定性。

Euler数学原理：

   Euler方法就是用差分方程初值问题的解来近似微分方程初值问题的解，即由下面公式依次算出的近似值。这组公式求微分问题的数值解称为向前Euler公式。

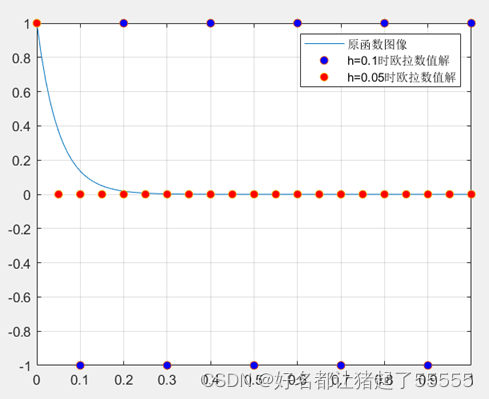
 步长分别为0.1和0.05的欧拉法数值解与此点对应的解析解误差的绝对值如下所示

结论：根据上面图像显示，欧拉法在计算数值解的过程中，有明显误差。当h=0.1时数值解稳定性明显低于h=0.05的时候。因此步长取值越大，导致的数值解误差波动越大。为了提高欧拉法在微分方程求解的精度，应适当缩短步长

2.取h=0.1和h=0.05，使用改进欧拉法计算，绘制出数值解和精确解图形，观察数值解的稳定性。

改进欧拉法数学原理：

 利用数值积分方法将微分方程离散化时，若用梯形公式计算式中之右端积分， 即

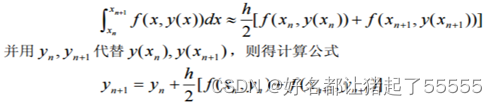
 直观上容易看出，用梯形公式计算数值积分要比矩形公式好。梯形公式为二阶方法。 梯形公式也是隐式格式，一般需用迭代法求解，迭代公式为

 按上式计算问题的数值解时，如果每步只迭代一次，相当于将 Euler 公式 与梯形公式结合使用：先用Euler公式求yn+1的一个初步近似值y，n+1. ，称为预测值，然 后用梯形公式校正求得近似值 yn+1，即

上称为由 Euler 公式和梯形公式得到的预测—校正系统，也叫改进 Euler 法。

为便于编制程序上机，上常改写成

本问使用改进欧拉法获得的函数图像如下图所示 

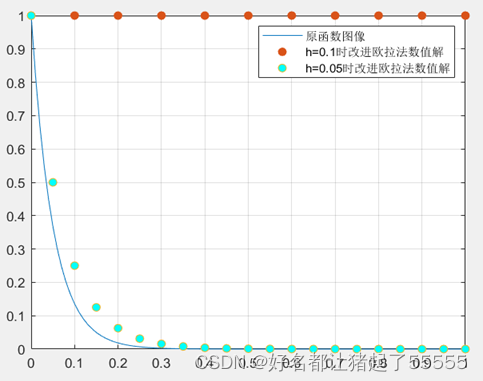
 步长分别为0.1和0.05的改进欧拉法数值解与此点对应的解析解误差的绝对值如下所示

 结论：根据上面图像显示，改进欧拉法在计算数值解的过程中，在步数较大的时候仍比 步数较小误差大。但是由于算法本身为二阶精度，数值计算结果稳定性明显比普通的欧拉法更好。

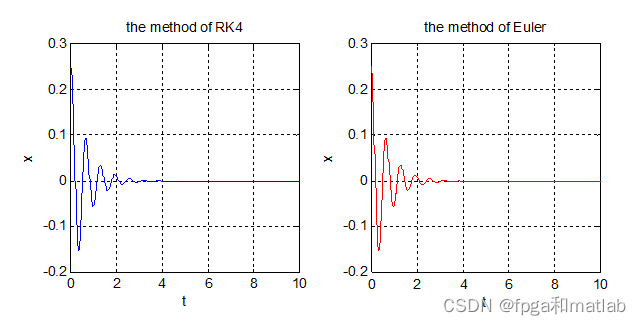
3.取h=0.1和h=0.05，使用经典四阶龙格库塔法计算，绘制出数值解和精确解图形，观察数值解的稳定性

龙格库塔法数学原理：

   龙格库塔法是一类数值解微分方程的算法，其中较常见的是四阶龙格库塔法。核心思想就是通过泰勒展开式进行消元，最后使得局部截断误差为5阶，算法精度达到四阶。具体公式如下

 使用四阶龙格库塔法获得的函数图像如下图所示

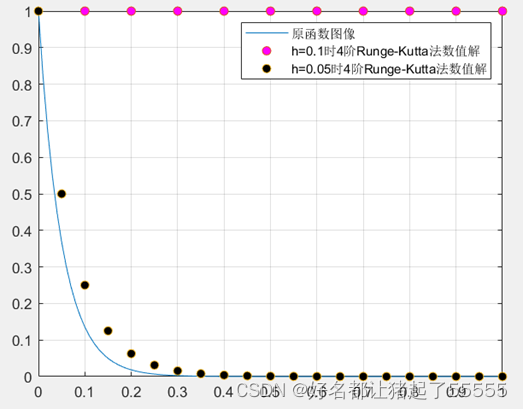
 步长分别为0.1和0.05的四阶龙格库塔法数值解与此点对应的解析解误差的绝对值如下所示

 结论：根据上面图像显示，四阶龙格库塔法的数值精度在原函数光滑性好的条件下精度最高（四阶）。但是依旧是步长越短，计算的误差越小。

附录：Matlab程序(主程序，欧拉法程序，改进欧拉法程序，四阶龙格库塔法程序，微分方程和原函数程序)

主程序

% Ordinary differential initial value problem
% 常微分初值问题数值解法
% 原函数的图像
h=0.01;%画图节点间距
x=[0:h:1];
k=1/h;
fx=zeros(1,k+1);
for i=1:k+1%将每一步长的x对应的解析解fy求出
fx(i)=primitive_fun(x(i));
end%使用欧拉法求解并画图[x1,y_Eu1,err_Eu1] = Euler_fun('differential_equation',0.1);
[x2,y_Eu2,err_Eu2] = Euler_fun('differential_equation',0.05);
plot(x,fx);
axis on
grid on
hold on
scatter(x1,y_Eu1,'markerfacecolor','b');
hold on
scatter(x2,y_Eu2,'markerfacecolor','r');
legend('原函数图像','h=0.1时欧拉数值解','h=0.05时欧拉数值解')
hold off%使用改进欧拉法求解并画图[x3,y_modEu1,err_modEu1] = modEu_fun('differential_equation',0.1);
[x4,y_modEu2,err_modEu2] = modEu_fun('differential_equation',0.05);
plot(x,fx);
axis on
grid on
hold on
scatter(x3,y_modEu1,'markerfacecolor','f');
hold on
scatter(x4,y_modEu2,'markerfacecolor','c');
legend('原函数图像','h=0.1时改进欧拉法数值解','h=0.05时改进欧拉法数值解')
hold off%使用=4阶Runge-Kutta法求解并画图[x5,y_RK41,err_RK41] = modEu_fun('differential_equation',0.1);
[x6,y_RK42,err_RK42] = modEu_fun('differential_equation',0.05);
plot(x,fx);
axis on
grid on
hold on
scatter(x5,y_RK41,'markerfacecolor','m');
hold on
scatter(x6,y_RK42,'markerfacecolor','k');
legend('原函数图像','h=0.1时4阶Runge-Kutta法数值解','h=0.05时4阶Runge-Kutta法数值解')
hold off

欧拉法程序

function [x,y_Eu,err] = Euler_fun(fun,h)
%使用欧拉法求解
% h为输入的步长,输出fx为原函数在步长h时所有自变量取值，y_Eu为使用欧拉法求出的数值解，err为解析解和数值解的差值绝对值
%本题x的定义域为[0,1]，因此运算次数为k
k=1/h;
%建立对应步长取值的x,y向量组，fx为在取得的每个节点的解析解
fx=zeros(1,k+1);
y_Eu=zeros(1,k+1);
err=zeros(1,k+1);
x=[0:h:1];
%将每一步长的x对应的解析解fy求出for i=1:k+1fx(i)=primitive_fun(x(i));end%计算出在步长为h条件下所有数值解
y_Eu(1)=1;%赋初值x(0)=0,y(0)=1;
for i=1:kf=feval(fun,y_Eu(i));y_Eu(i+1)=y_Eu(i)+h*f;
end
%计算解析解与数值解直接的误差
for i=1:k+1err(i)=abs(y_Eu(i)-fx(i));
end
end

改进欧拉法程序

function [x,y_modEu,err] = modEu_fun(fun,h)
%使用改进欧拉法求解
% h为输入的步长,输出fx为原函数在步长h时所有自变量取值，y_Eu为使用改进欧拉法求出的数值解，err为解析解和数值解的差值绝对值
%本题x的定义域为[0,1]，因此运算次数为k
k=1/h;
%建立对应步长取值的x,y向量组,fx为在取得的每个节点的解析解
fx=zeros(1,k+1);
y_modEu=zeros(1,k+1);
err=zeros(1,k+1);
x=[0:h:1];
%将每一步长的x对应的解析解fy求出for i=1:k+1fx(i)=primitive_fun(x(i));end
%计算出在步长为h条件下所有数值解
y_modEu(1)=1;%赋初值x(0)=0,y(0)=1;
for i=1:kf1=h*feval(fun,y_modEu(i));f2=h*feval(fun,y_modEu(i)+f1);y_modEu(i+1)=y_modEu(i)+0.5*(f1+f2);
end
%计算解析解与数值解直接的误差
for i=1:k+1err(i)=abs(y_modEu(i)-fx(i));
end
end

四阶龙格库塔法程序

function [x,y_RK4,err] = Ru_Ku4(fun,h)
%使用4阶Runge-Kutta法求解
% h为输入的步长,输出x为原函数在步长h时所有自变量取值，y_RK4为使用改进欧拉法求出的数值解，err为解析解和数值解的差值绝对值
%本题x的定义域为[0,1]，因此运算次数为k
k=1/h;
%建立对应步长取值的x,y向量组,fx为在取得的每个节点的解析解
fx=zeros(1,k+1);
y_RK4=zeros(1,k+1);
err=zeros(1,k+1);
x=[0:h:1];
%将每一步长的x对应的解析解fy求出for i=1:k+1fx(i)=primitive_fun(x(i));end
%计算出在步长为h条件下所有数值解
y_RK4(1)=1;%赋初值x(0)=0,y(0)=1;
for i=1:kK1=h*feval(fun,y_RK4(i));K2=h*feval(fun,y_RK4(i)+K1*0.5);K3=h*feval(fun,y_RK4(i)+K2*0.5);K4=h*feval(fun,y_RK4(i)+K3);y_RK4(i+1)=y_RK4(i)+(K1+2*(K2+K3)+K4)/6;
end
%计算解析解与数值解直接的误差
for i=1:k+1err(i)=abs(y_RK4(i)-fx(i));
end
end

微分方程和原函数程序

function f= differential_equation(y)
%大作业6一直使用的微分方程
f=-20*y;
endfunction f = primitive_fun(x0)
%方程原函数
%求解此微分方程原函数
syms y(x)
eqn = diff(y,x) == -20*y;
cond = y(0) == 1;
y(x) = dsolve(eqn,cond);
f=y(x0);
end