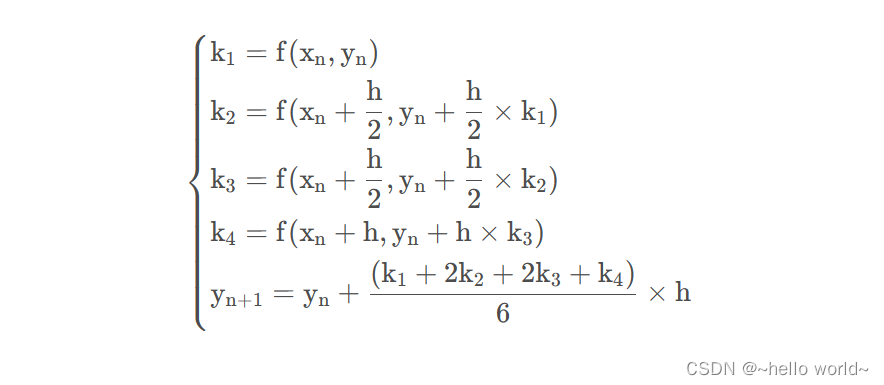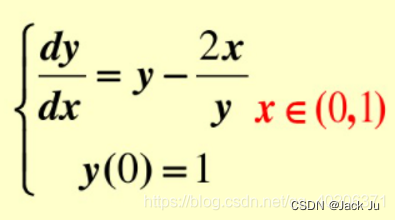龙格库塔法的原理

 在百度百科中是这么解释的：在各种龙格－库塔法当中有一个方法十分常用，以至于经常被称为“RK4”或者就是“龙格－库塔法”。该方法主要是在已知方程导数和初值信息，利用计算机仿真时应用，省去求解微分方程的复杂过程。

令初值问题表述如下。
$$y^{\prime }=f(x_n,y_n)，y(x_0)=y_0$$
 则，对于该问题的RK4由如下方程给出：
$$y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)$$
 其中，
$$k_1=f(x_n,y_n)$$
$$k_2=f(x_n+\frac{h}{2},y_n+\frac{h}{2}{k}_1)$$
$$k_3=f(x_n+\frac{h}{2},y_n+\frac{h}{2}{k}_2)$$
$$k_4=f(x_n+h,y_n+h{k}_3)$$
 我开始在理解的时候花了挺长时间，毕竟公式很难让人理解，因此我才想把我遇到的困难和理解写下来，帮助大家理解龙格库塔这个方法。
 在我看来龙格库塔方法就是改良之后的欧拉法，求解精度更高。就是用已知点和所求点这两个点之间几个点的斜率，加权平均后得出的斜率就为所求点与已知点的斜率。

 上图就是我所举的例子，事实上我们只知晓$y^{\prime }$,即$k_1$,$k_2$,$k_3$,$k_4$,以及$y_0$。这样我们就可以通过四阶龙格库塔方法进行不断迭代，求出$y_1,y_2\dots y_n$。

利用四阶龙格库塔法求解一个案例

  如$y^{\prime }=x+xy$这样一个表达式，我们若用正常的数学方法求解或许并不困难。但是一旦表达式变得很复杂， 例如$y^{\prime }=\sin (x)\cos (y)+xy$这样的微分方程,求解起来就会相当麻烦。因此利用龙格库塔法求解，会使问题变得较简单方便。一般我们使用四阶龙格库塔方程解决问题，这样求解的精度较高，且求解速度较快。
  我们举$y=x+xy$这样一个简单的微分方程来说明一下，由于$y^{\prime }=f(x,y)$,因此$f(x,y)=\frac{dy}{dx}=x+xy$，我们需要知道$y(x_0)=y_0$为多少，在此案例中,我们设$x_0=0$,$y(0)=y_0=0$,我们设步长$h=0.1$，计算公式如下所示：
$$k_1=f(x_0,y_0)=f(0,0)=0+0=0$$

$$k_2=f(x_0+\frac{h}{2},y_0+k_1\times \frac{h}{2})=f(0+0.05,0+0\times 0.05)=0.05+0=0.05$$

$$k_3=f(x_0+\frac{h}{2},y_0+k_2\times \frac{h}{2})=f(0+0.05,0+0.05\times 0.05)=0.05+0.05\times 0.0025=0.050125$$
$$k_4=f(x_0+\frac{h}{2},y_0+k_3\times \frac{h}{2})=f(0+0.1,0+0.050125\times 0.1)=0.1+0.1\times 0.050125=0.10050125$$
$$y_1=y_0+\frac{h}{6}(k_1+2k_2+2k_3+k_4)\approx 0+\frac{0.1}{6}\times 0.3008=0.0050$$
  到此我们已经求出$y_1=0.0050$，就可把$y_1$带入下一步继续迭代，可是有的同学就会问$x_1$等于多少，由于我们设的步长$h=0.1$,因此$x_1=x_0+h=0.1$,扩展后则为$x_n=x_0+nh$。
 我们需要验通过四阶龙格库塔法求解的值准不准确，因此我们用经典的微分方程解法去求解，求解过程如下：
$$y^{\prime }=\frac{dy}{dx}=x+xy$$
$$\frac{dy}{dx}=x(1+y)$$
$$\frac{dy}{1+y}=xdx$$
 两边同时积分
$$\ln (1+y)=\frac{1}{2}{x}^2+C$$
$$y=e^{\frac{1}{2}{x}^2}+C$$
 我们设$x_0=0$时，$y_0=0$,因此$C=-1$，即$y=e^{\frac{1}{2}{x}^2}-1$,当$x_1=0.1$时，$y_1=0.0050$。验证后我们发现四阶龙格库塔法的精确度确实很高。

用MATLAB编程

clc,clear;
syms x y %设置符号变量x,y
f(x,y)=x*y+x;
z(x)=exp(1/2*x^2)-1%我们计算得出的方程，用于验算
df=f;
y0=0;%设y0=0
a=0;%设起始点
b=3;%设终点
h=0.1;%设步长
[x1,y1]=FourLongkuta(df,y0,a,b,h);%用四阶龙格库塔法求解
figure
plot(a:h:b,z(a:h:b))
hold on
plot(a:h:b,y1,'r')
legend('原函数','龙格库塔法')
hold off

 下面是四阶龙格库塔方法的函数：

function [x1,y1]=FourLongkuta(df,y0,a,b,h)%从左到右依次为已知的导函数，初始函数值，初始横坐标值，终止横坐标值，步长
n=floor((b-a)/h);%求解所需的总步长，floor的用法是取一个小数的最小整数值
y1(1)=y0;%赋值y1(1)=y(t0),且数为双精度，这样以后计算的符号值都会转换成双精度
x1=a:h:b;%设xn的值
for i=1:n%龙格库塔方法进行数值求值      k1=double (df( x1(i),y1(i) ) ) ;%double将符号值转为双精度值可以提高运算速度k2=double (df( x1(i)+h/2,y1(i)+k1*h/2 ) );k3=double (df( x1(i)+h/2,y1(i)+k2*h/2 ) );k4=double (df( x1(i)+h,y1(i)+k3*h ) );y1(i+1)=y1(i)+h*(k1+2*k2+2*k3+k4)/6;   
end
end

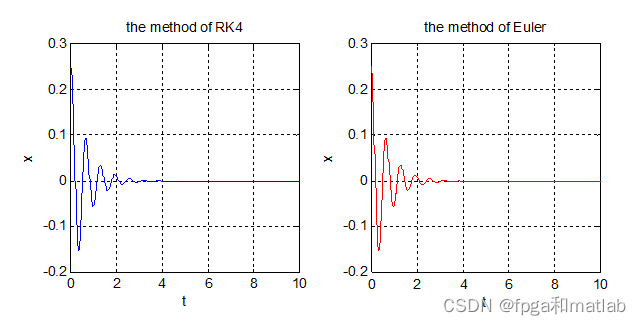
 由图可以看到四阶龙格库塔法的精度很高，几乎覆盖在原函数上。
 创作不易，请大家多多支持！