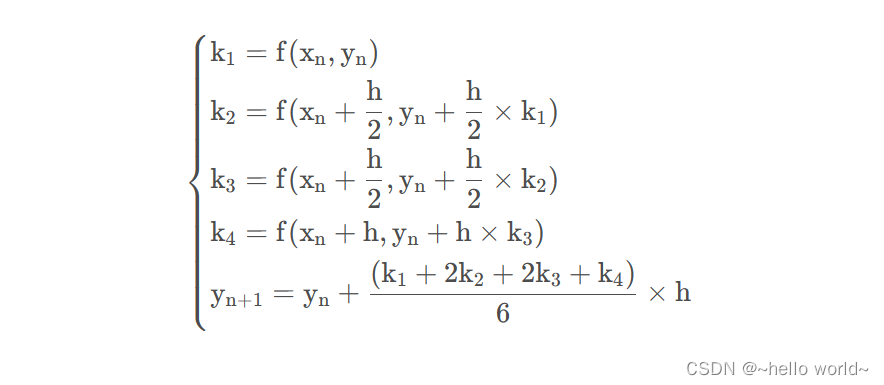常微分方程

Ordinary differential equation，简称ODE，自变量只有一个的微分方程。
例子1： $\frac{dy}{dx}=f(x,y)$ ,$f(x,y)$是已知函数

偏微分方程

Partial differential equation，简称PDE，自变量有多个的微分方程。
例子2：$u_t-a^2{u}_{xx}=0,a>0$为常数（热传导方程，抛物型方程的典型代表）

显式（Explicit）

第n步结果可以从n-1, n-2, …1步的结果直接推导出来，迭代时每步的计算量很小，但迭代增量也有限制，不能太大，否则会出现发散。

隐式（Implicit）

第n步的计算结果不能直接从前面的结果推导出来，必须做进一步的求解，这样，迭代时每步的计算量很大。

泰勒公式

$$f(x)=\frac{f(a)}{0!}+\frac{f^{\prime }(a)}{1!}(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+...+\frac{f^{(n)}(a)}{n!}(x-a{)}^n+R_n(x)$$
称为 f(x) 在 x = a 点关于 x 的幂函数展开式，又称为 Taylor 公式，式中Rn（x）叫做 Lagrange 余项。

欧拉方法

考虑一阶常微分方程的初值问题
$$\{\begin{array}{rl}& \frac{dy}{dx}=f(x,y)\\ & y(x_0)=y_0\end{array}$$

前向欧拉法

$$y_{n+1}=y_n+hf(x_n,y_n),n=0,1,...$$

后向欧拉算法

$$y_{n+1}=y_n+hf(x_{n+1},y_{n+1}),n=0,1,...$$
前后向欧拉法的推理、举例及稳定性对比的超棒分析！地址入口

梯形公式

$$y_{n+1}=y_n+\frac{h}{2}[f(x_n+y_n)+f(x_{n+1}+y_{n+1})],n=0,1,...$$

改进的欧拉算法

$$\{\begin{array}{rl}& {\hat{y}}_{n+1}=y_n+hf(x_n,y_n)\\ & y_{n+1}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},{\hat{y}}_{n+1})]\end{array}$$
也可以表示成
$$\{\begin{array}{rl}& y_f=y_n+hf(x_n,y_n)\\ & y_b=y_n+hf(x_{n+1},y_f)\\ & y_{n+1}=\frac{1}{2}(x_f+x_b)\end{array}$$

其中$y_f$表示利用向前(显式)欧拉公式的近似值，$y_b$表示利用向后(隐式)欧拉公式的近似值(利用了$y_f$)，最后取平均值。
上面利用$f(x_{n+1},{\hat{y}}_{n+1})]$是有误差的，也可通过多次迭代减少误差，具体公式如下
$$\{\begin{array}{rl}& {\hat{y}}_{n+1}^{(0)}=y_n+hf(x_n,y_n)\\ & y_{n+1}^{(k+1)}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},{\hat{y}}_{n+1}^{(k)})],k=0,1,2,...\end{array}$$

其中，后向欧拉算法和梯形公式是隐式算法，前向欧拉算法和改进的欧拉算法是显式算法。欧拉算法计算容易，但是精度低，梯形公式精度高，但是是隐式形式，不易求解。将两式结合，则可以得到改进的欧拉公式。先用欧拉公式求出yn+1的一个粗糙的估计值，再用梯形方法进行精确化，称为校正值。

四阶龙格库塔算法（Runge-kutta method）

$$\{\begin{array}{rl}& k_1=f(x_n,y_n)\\ & k_2=f(x_n+\frac{h}{2},y_n+\frac{h}{2}\times k_1)\\ & k_3=f(x_n+\frac{h}{2},y_n+\frac{h}{2}\times k_2)\\ & k_4=f(x_n+h,y_n+h\times k_3)\\ & y_{n+1}=y_n+\frac{(k_1+2k_2+2k_3+k_4)}{6}\times h\end{array}$$
龙格-库塔算法是一种在工程上应用广泛的高精度单步算法，算法精度较高，如果预先取四个点就是四阶龙格-库塔算法。
真的！龙格库塔算法的超强解析！地址入口

四阶龙格库塔函数代码

runge_kuttx0_o4.m
代码参考的博客地址入口
总结一下代码的优点~
1、使用函数句柄，方便复用~
2、模仿了ode45的函数输入变量，和ode45用起来差不多~

function [t,y,n]=runge_kuttx0_o4(ufunc,tspan,y0,h)%参数表顺序依次是微分方程组的函数名称，时间起点终点,初始值，步长（参数形式参考了ode45函数）
if nargin<4h=0.01;
end
if size(tspan)==[1,2]t0=tspan(1);tn=tspan(2);
elseerror(message('MATLAB:runge_kuttx0_o4:WrongDimensionOfTspan'));
end
n=floor((tn-t0)/h);%求步数
t(1)=t0;%时间起点
y(:,1)=y0;%第一列赋初值，可以是向量，代表不同的初始值
for i=1:n
t(i+1)=t(i)+h;
k1=ufunc(t(i),y(:,i));
k2=ufunc(t(i)+h/2,y(:,i)+h*k1/2);
k3=ufunc(t(i)+h/2,y(:,i)+h*k2/2);
k4=ufunc(t(i)+h,y(:,i)+h*k3);
y(:,i+1)=y(:,i)+h*(k1+2*k2+2*k3+k4)/6;
%按照龙格库塔方法进行数值求解
end

test1.m

clear
clc
test_fun=@(t,y)(y+3*t)/t^2;
tspan=[1 4];
y0=-2;
h=1;
[t1,y1]=ode45(test_fun,tspan,y0);
[t2,y2]=runge_kuttx0_o4(test_fun,tspan,y0,h);
plot(t1,y1,'r',t2,y2,'g')
legend('ode45函数效果','自编四阶龙格库塔函数效果')
xlabel('t');
ylabel('y');
title('效果对比图')

test.m运行结果

步长选择

之前讨论的所有的龙格-库塔方法都是以$\Delta t$定步长来展开的，但从$x_i\Rightarrow x_{i+1}$单步递推过程来说，步长$\Delta t$越小，局部截断误差越小(方法确定情况下)，但是随着步长的缩小，不但会引起计算量的增加，而且也有可能引起舍入误差的严重积累；但步长$\Delta t$太大又不能达到预期的精度要求，所以选择合适的步长$\Delta t$，在实际计算中也是比较重要的。其实有时候在实际使用中步长并不需要算法确定，而是需要根据数据帧率来确定的，比如imu数据。??
下面给出求解步长的步骤：

1、以步长$\Delta t$开始，利用龙格-库塔公式计算$x_i\Rightarrow x_{i+1}$得到一个近似值$x_{i+1}^{\Delta t}$；
2、然后步长减半为$\Delta t/2$，利用龙格-库塔公式分两步计算$x_i\Rightarrow x_{i+\frac{1}{2}}\Rightarrow x_{i+1}$得到一个近似值$x_{i+1}^{\Delta t/2}$；
3、计算$\mid x_{i+1}^{\Delta t/2}-x_{i+1}^{\Delta t}<ϵ\mid$是否成立，如果成立直接步长选择$\Delta t$，否则继续步长减半，重复上诉步骤直到满足精度要求。
test2.m

clear
clc
test_fun=@(t,y)(y+3*t)/t^2;
tspan=[1 15];
y0=-2;
h=1;
acc=0.0001;
[t1,y1,n1]=runge_kuttx0_o4(test_fun,tspan,y0,h);
tf=t1;yf=y1;hf=h;
h=h/2;
[t2,y2,n2]=runge_kuttx0_o4(test_fun,tspan,y0,h);
while(sum(abs(y1(2:n1+1)-y2(3:2:n2+1)))/n1>=acc)
t1=t2;y1=y2;n1=n2;
h=h/2;
[t2,y2,n2]=runge_kuttx0_o4(test_fun,tspan,y0,h);
end
plot(tf,yf,'r',t2,y2,'g')
legend(['四阶龙格库塔初始步长下的效果,h=',num2str(hf)],['四阶龙格库塔精度约为0.01的效果,h=',num2str(h*2)])
xlabel('t');
ylabel('y');
title('效果对比图')