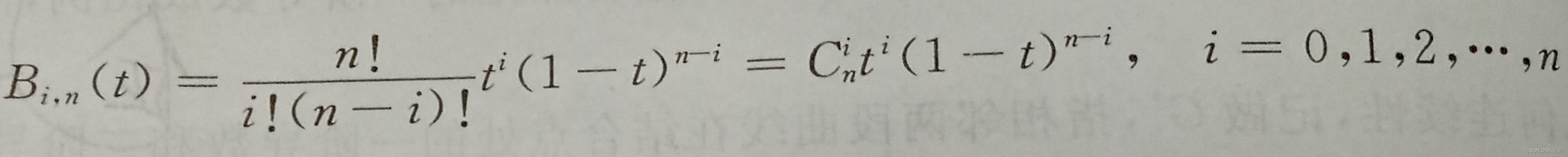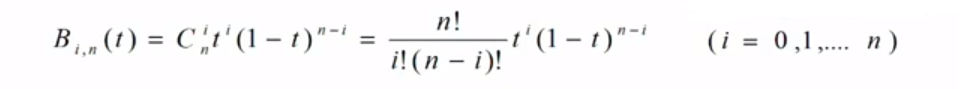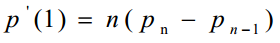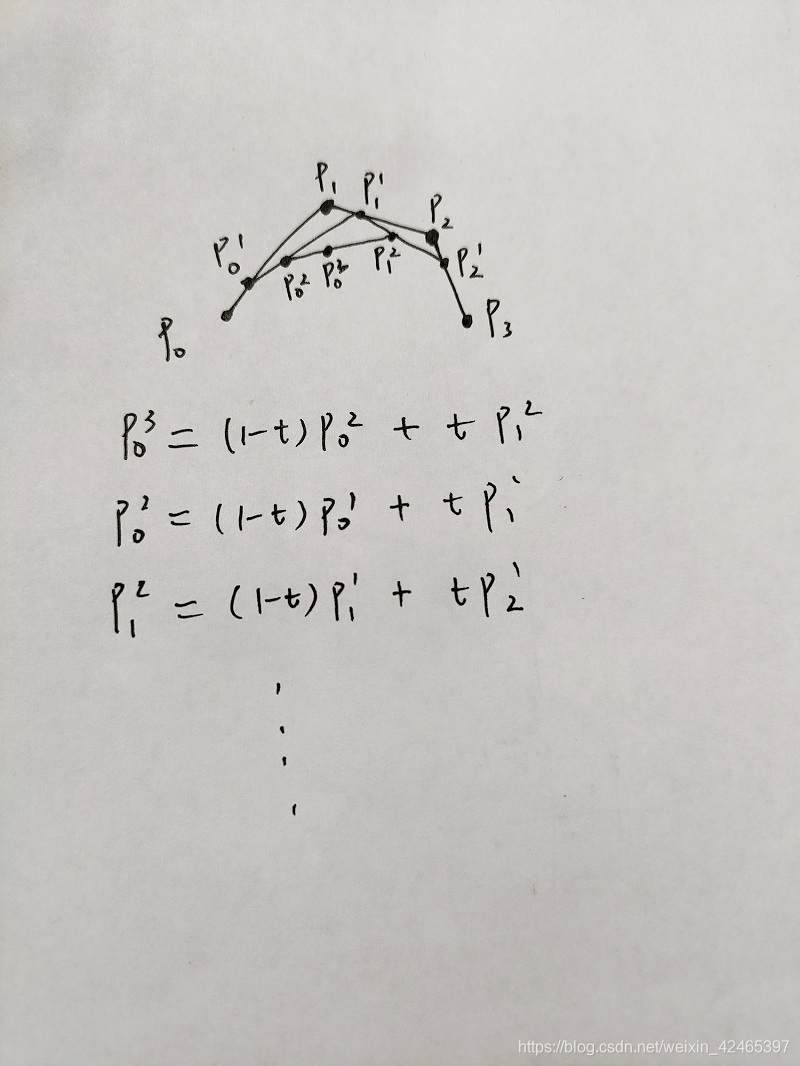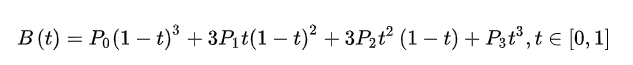贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具，如PhotoShop等。在Flash4中还没有完整的曲线工具，而在Flash5里面已经提供出贝塞尔曲线工具。
贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。

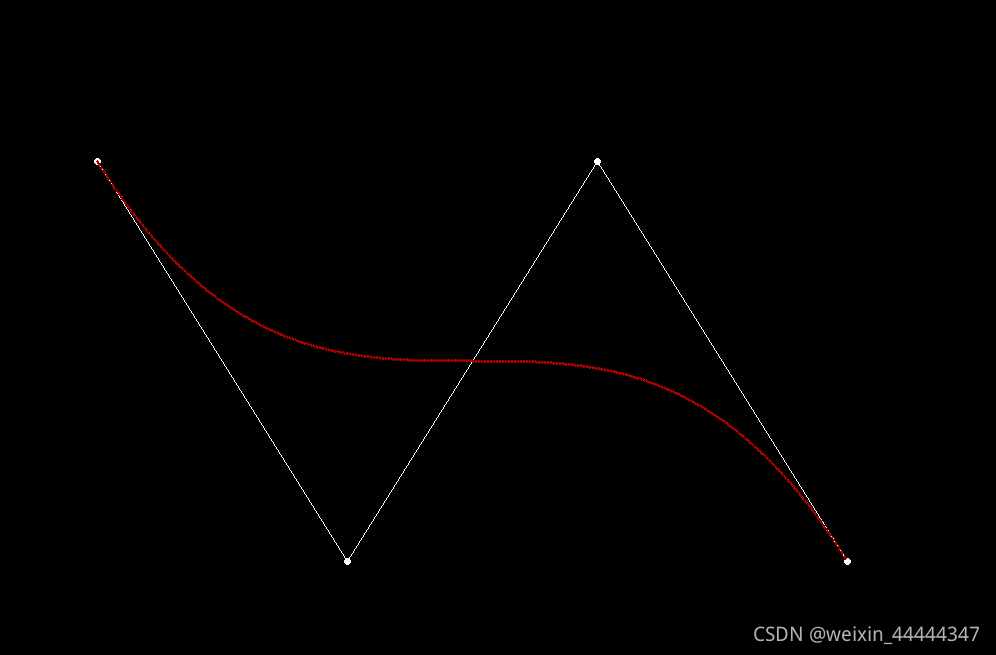
下面我们展示用js绘制贝塞尔曲线（Bézier-Curve）,效果图如下：

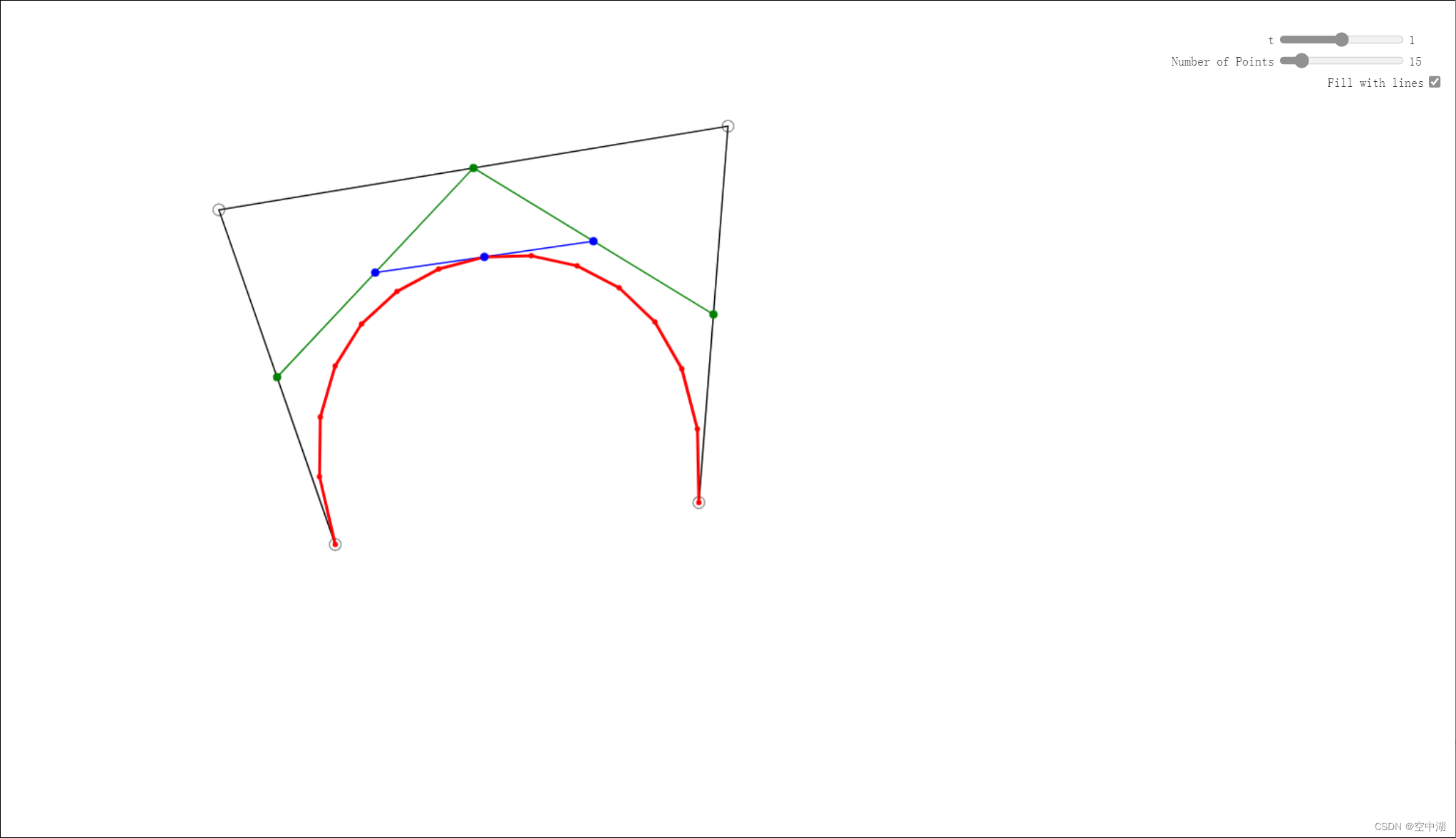
 在线demo地址

代码：BezierCurve.js

var canvas = document.querySelector('#canvas');
const ctx = canvas.getContext('2d');var width = canvas.clientWidth;
var height = canvas.clientHeight;// Setting the size of canvas when loading the page to fully fit it and draw
window.addEventListener('load', () => {canvas.height = canvas.clientHeight;canvas.width = canvas.clientWidth;draw(ctx);
})// Resizing canvas when page is resized 
window.addEventListener('resize', () => {canvas.height = canvas.clientHeight;canvas.width = canvas.clientWidth;width = canvas.clientWidth;height = canvas.clientHeight;draw(ctx);
})// UIlet settings = {t: 0.5,numPoints: 15,fill_lines: 1
}
webglLessonsUI.setupUI(document.querySelector('#ui'), settings, [{type: 'slider', key: 't', min: 0,    max: 1, step: 0.01, slide: (event, ui) => {settings.t = ui.value;ctx.clearRect(0, 0, canvas.width, canvas.height);draw();}},{type: 'slider', key: 'numPoints', name: 'Number of Points', min: 2,    max: 100, slide: (event, ui) => {settings.numPoints = ui.value;ctx.clearRect(0, 0, canvas.width, canvas.height);draw();}},{type: 'checkbox', key: 'fill_lines', name: 'Fill with lines', min: 2,    max: 100, change: (event, ui) => {ctx.clearRect(0, 0, canvas.width, canvas.height);draw();}}
]);// Setting variablesvar points = [[0.23 * width, 0.65 * height],[0.15 * width, 0.25 * height],[0.5 * width, 0.15 * height],[0.48 * width, 0.60 * height]
]var circle_width = 0.5;
var line_width = 1.5;
var radius = 4;
var move = 0;// Main function that will handle all drawings
function draw() {// Draws the control points and the linesfor (let i=0; i<4; i++) drawCircle(ctx, points[i], 0, circle_width, 'black', 6);drawLines(ctx, points, 4, line_width, 'black');let t = settings.t;// Each point in Q will be the corresponding t point between each pair of control pointslet Q = [];for (let i=0; i<3; i++) {Q.push([(1-t) * points[i][0] + t * points[i+1][0], (1-t) * points[i][1] + t * points[i+1][1]]);}for (let i=0; i<3; i++) drawCircle(ctx, Q[i], 1, circle_width, 'green', radius);drawLines(ctx, Q, 3, line_width, 'green');// We do the same for the resulting pointslet R = [];for (let i=0; i<2; i++) {R.push([(1-t) * Q[i][0] + t * Q[i+1][0], (1-t) * Q[i][1] + t * Q[i+1][1]]);}for (let i=0; i<2; i++) drawCircle(ctx, R[i], 1, circle_width, 'blue', radius);drawLines(ctx, R, 2, line_width, 'blue');// Finally we do the same for those 2 points and compute the t point between. That will be// be the point that belongs to the Bezier curvelet M = [(1-t) * R[0][0] + t * R[1][0], (1-t) * R[0][1] + t * R[1][1]];// Computes the specified number of points of the Bezier curve, draws them and// fills with lines between the points to generate an approximation of the curve.let bezier_pts = getPointsOnBezierCurve(points, settings.numPoints);for (let i=0; i<settings.numPoints; i++) drawCircle(ctx, bezier_pts[i], 1, circle_width, 'red', 2.5);if (settings.fill_lines) drawLines(ctx, bezier_pts, settings.numPoints, 3, 'red');// Draws M on top of the curvedrawCircle(ctx, M, 1, circle_width, 'blue', radius);
}// EVENTS:// Variable that will contain which point is clicked to move
var pt = 0;
document.addEventListener('mousedown', (event) => {let x = event.clientX;let y = event.clientY;// Checks which point is being pressedfor (let i=0; i<4; i++) {if(dist([x, y], points[i]) < 10) {move = 1;pt = i;}}
})// Sets move to 0 when the mouse button is up
document.addEventListener('mouseup', (event) => {move = 0;
})// Moves the selected point when the mouse button is pressed
document.addEventListener('mousemove', (event) => {let x = event.clientX;let y = event.clientY;if(move == 1) {points[pt] = [x, y];ctx.clearRect(0, 0, canvas.width, canvas.height);draw();}
})