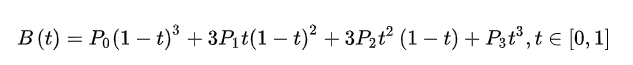前言：

        作为rhino重度用户，我对于nurbs建模早有耳闻，但对于何为nurbs却不得其解。最近借上《计算机辅助设计》课程的机会，对此作了一些深入的学习，于是在此记录一下一些课程笔记和课后思考。了解nurbs，主要对于三个概念的理解：bezier曲线、B样条曲线、nurbs曲线与曲面。本文先介绍一下bezier曲线，分为原理解释和代码分享（c++）两部分。

bezier曲线原理

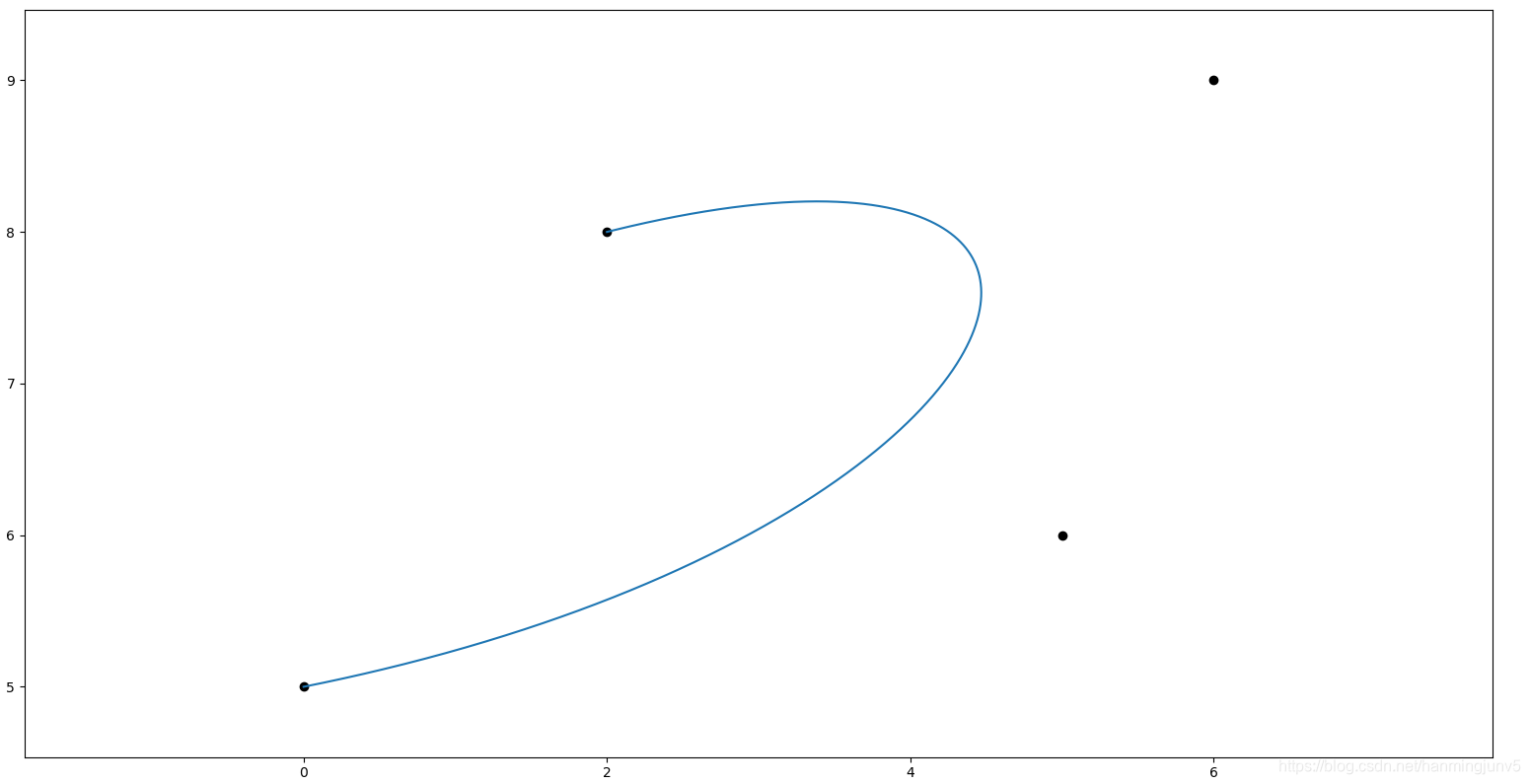
        自由曲线的一般绘制方法是先画控制点，再由控制点共同作用得到曲线。

        

 

         也就是说曲线上每个点的坐标可以由控制点坐标映射得到。 即：

         伯恩斯坦基底多项式

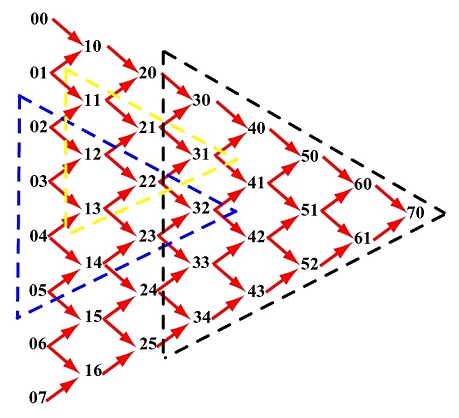
        所以关键在于系数B应该如何确定，bezier曲线使用伯恩斯坦基底作为系数。以下是伯恩斯坦基底多项式的表达式：

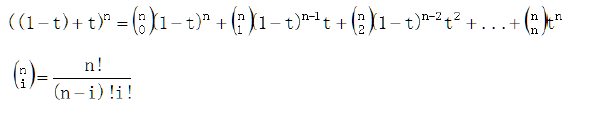
         bezier曲线参数方程

        用控制点的坐标乘以对应的伯恩斯坦基底，就得到了bezier曲线的参数方程。

         

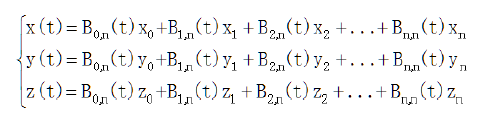
也可以写作：

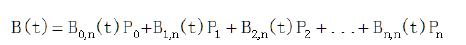
         即：

 

        有理bezier曲线

        刚刚的公式描述的bezier曲线是均匀的，每个控制点的权重相同。我们可以为每个控制点设置一个权重，这样得到了有理bezier曲线。

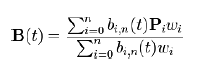
        w表示对应控制点的权重

代码分享

        我用c++实现了简单的bezier曲线绘制，由于c++绘图太麻烦，这里还使用了easyx库。由于只是为了理解原理，所以我是通过画出曲线上100个点的位置，来代表曲线。核心代码如下：（这里要注意，公式里的n指的是曲线的次数，等于控制点数量-1。）

void bezier(POINT *pts,int len) {//绘制bezier曲线int n = len - 1;//公式中的n是控制点数减一for (double t = 0;t < 1;t += 0.002) {double Bt = 0;double Xt = 0;double Yt = 0;for (int i = 0;i <= n; i++) {Bt = fact(n)/(fact(n-i)*fact(i))*pow((1-t),(n-i))*pow(t,i);//计算伯恩斯坦基底Xt += Bt * (pts[i].x);Yt += Bt * (pts[i].y);}fillcircle(Xt, Yt, 1);}
}

 完整代码如下：

#include <graphics.h>    // Reference graphics library header file
#include <conio.h>
#include<iostream>
#include<math.h>
using namespace std;
​
int fact(int n) {//阶乘函数if (n == 0) {return 1;}else {int res = 1;for (int i = n;i > 0;i--) {res *= i;}return res;}
}
​
void bezier(POINT *pts,int len) {//绘制bezier曲线int n = len - 1;//公式中的n是控制点数减一for (double t = 0;t < 1;t += 0.002) {double Bt = 0;double Xt = 0;double Yt = 0;for (int i = 0;i <= n; i++) {Bt = fact(n)/(fact(n-i)*fact(i))*pow((1-t),(n-i))*pow(t,i);//计算伯恩斯坦基底Xt += Bt * (pts[i].x);Yt += Bt * (pts[i].y);}fillcircle(Xt, Yt, 1);}
}
​
int main()
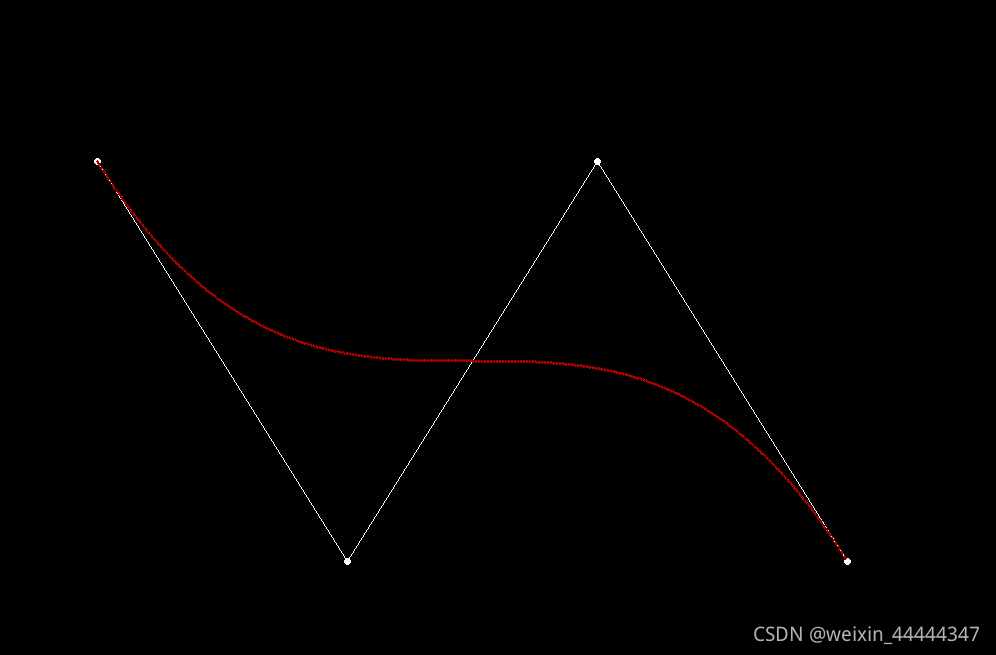
{initgraph(1000,800);  // 创建画布POINT a[] = { {100,200},{350,600},{600,200},{850,600} };int len = sizeof(a) / sizeof(a[0]);setfillcolor(WHITE);//设置画笔颜色、填充颜色setlinecolor(WHITE);for (int i = 0;i < len;i++) {fillcircle(a[i].x, a[i].y, 3);//画出控制点的位置}polyline(a,4);//画出控制点的连线
​setfillcolor(RED);//设置画笔颜色、填充颜色setlinecolor(RED);bezier(a,len);//绘制bezier曲线_getch();        // Press any key to continueclosegraph();      // Close the graphics windowreturn 0;
}

        运行效果如下：