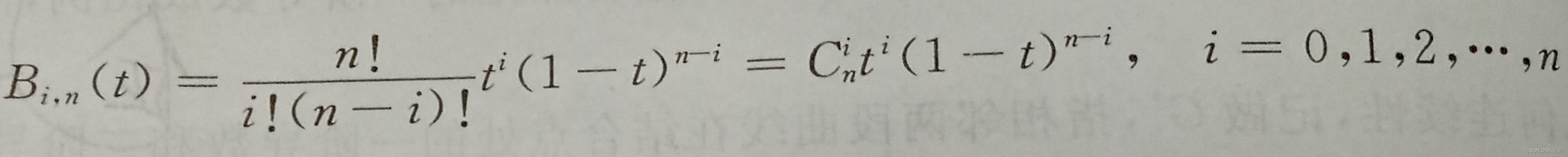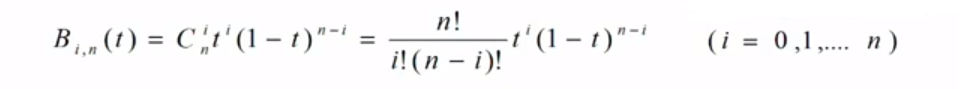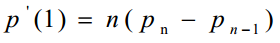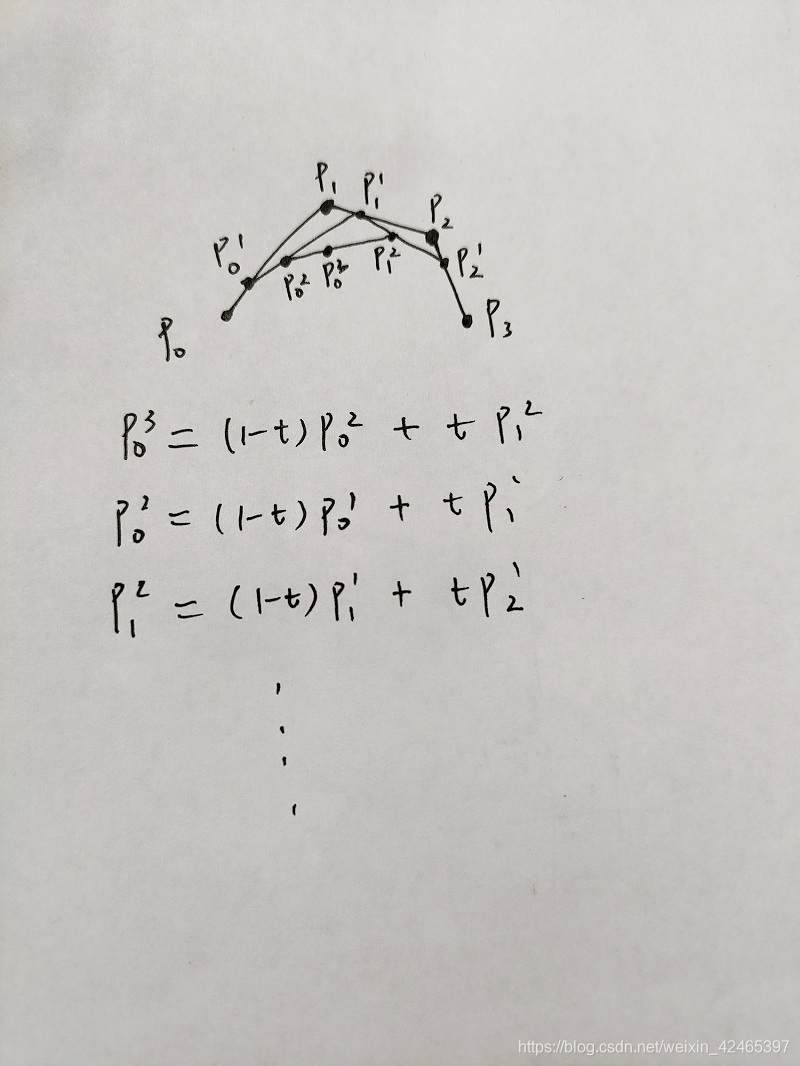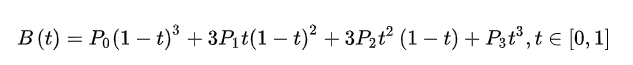贝塞尔曲线（Bezier Curve）原理、公式推导及matlab代码实现

article/2025/11/9 17:46:29

1. 定义
贝塞尔曲线(Bezier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具，如PhotoShop等。

贝塞尔曲线的一些特性：

使用n个控制点 ${\{P_1,P_2,...,P_n\}}$ 来控制曲线的形状
曲线经过起点 ${P_1}$ 和终点 $P_n$ ，但不经过中间点 $P_2$ ~ $P_{n-1}$

2.直观理解

step1：在二维平面内选三个不同的点并依次用线段连接

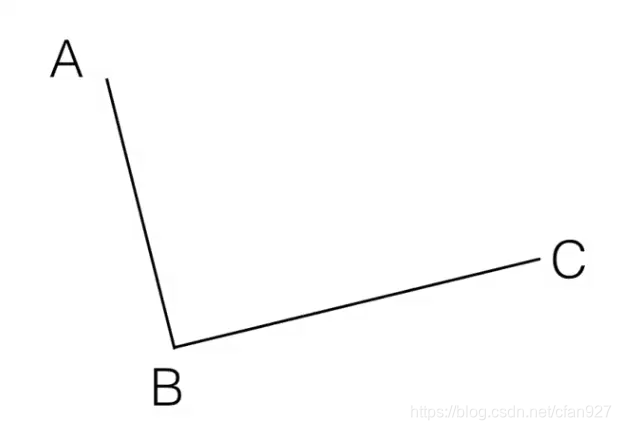
在这里插入图片描述

step2：在线段AB和BC上找到D、E两个点，使得 $\frac{AD}{DB}=\frac{BE}{EC}$

Step3：连接DE，并在DE上找到F点，使其满足 $\frac{DF}{FE}=\frac{AD}{DB}=\frac{BE}{EC}$ (抛物线的三切线定理)

Step4.找出符合上述条件的所有点

在这里插入图片描述

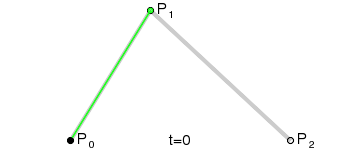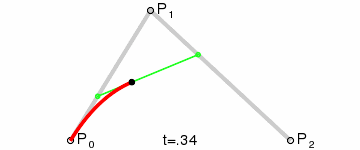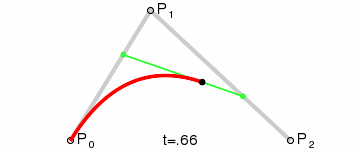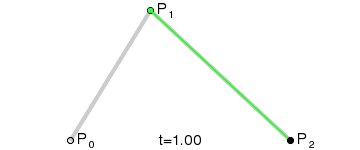
上述为一个二阶贝塞尔曲线。同样的，也有n解贝塞尔曲线

曲线	图示
一阶
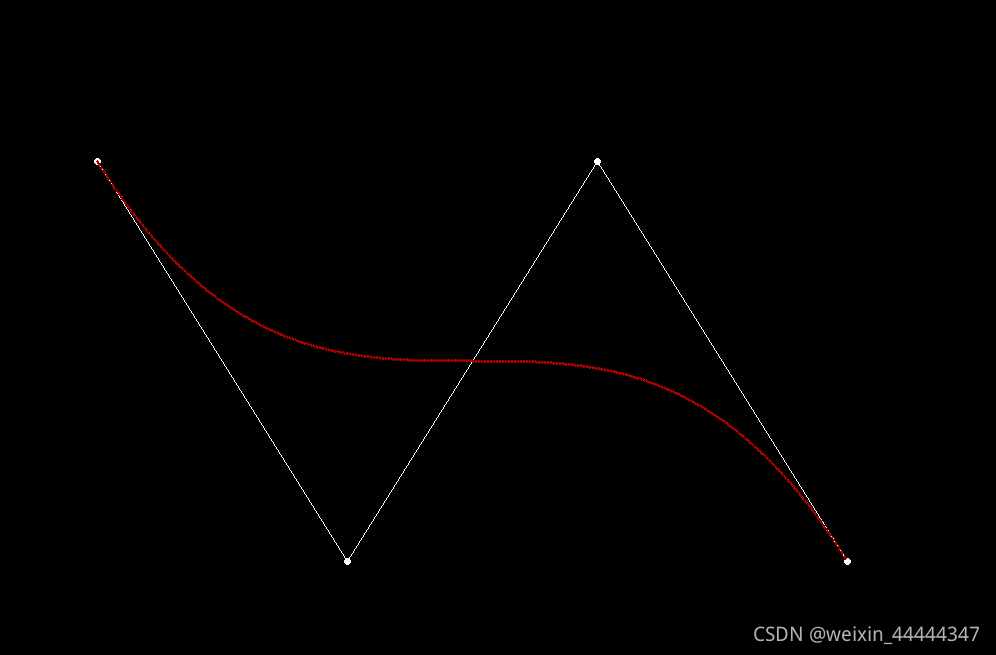
三阶
四阶
五阶

3.公式推导

3.1一次贝塞尔曲线（线性公式）

定义：给定点 $P_0$ , ${P_1}$ ,线性贝塞尔曲线只是一条两点之间的直线，这条线由下式给出，且其等同于线性插值：

$B(t)=P_0+(P_1-P_0)t=(1-t)P_0+tP_1,t\in [0,1]$

其中，公式中的 $P_0$ , ${P_1}$ 同步表示为横或纵坐标。

假设 $P_0$ 坐标为 $(a,b)$ , ${P_1}$ 的坐标为 $(c,d)$ , $P_2$ 的坐标为（x,y）,则有

$\frac{x-a}{c-x}=\frac{t}{1-t}\Rightarrow x=(1-t)a+tc$ (3-1)

同理，有：

$\frac{y-b}{d-y}=\frac{t}{1-t}\Rightarrow y=(1-t)b+td$ (3-2)

于是可将（3-1）（3-2）可简写为

$B(t)=(1-t)P_0+tP_1,t\in [0,1]$

3.2 二次贝塞尔曲线（二次方公式）

定义：二次贝塞尔曲线的路径由给定点 $P_0$ ， ${P_1}$ ， $P_2$ 的函数B(t）给出：

$B(t)=(1-t)^2P_0+2t(1-t)P_1+t^2P_2,t\in [0,1]$

假设 $P_0$ ${P_1}$ 上的点为A， ${P_1}$ $P_2$ 上的点为B，AB上的点为C（也即C为曲线上的点）。则根据一次贝塞尔曲线公式有：

$A=(1-t)P_0+tP_1$

$B=(1-t)P_1+tP_2$

$C=(1-t)A+tB$

将上式中的A、B带入C中，即可得到二次贝塞尔曲线的公式：

$B(t)=(1-t)^2P_0+2t(1-t)P_1+t^2P_2 , t\in [0,1]$

3.3 二次贝塞尔曲线（三次方公式）

同理可得三次贝塞尔曲线公式：

$B(t)=(1-t)^3P_0+3t(1-t)^2P_1+3t^2(1-t)P_2+t^3P_3 , t\in [0,1]$

3.4 n次贝塞尔曲线（一般参数公式）

定义：给定点 $P_0$ , $P_1$ ,..., $P_n$ ，则n次贝塞尔曲线由下式给出：

$B(t)=\sum_{i=0}^{n}\binom{n}{i}P_i(1-t)^{n-i}t^i=\binom{n}{0}P_0(1-t)^{n}t^0+\binom{n}{1}P_1(1-t)^{n-1}t^1+...+\binom{n}{n-1}P_{n-1}(1-t)^{n-1}t^{n-1}+\binom{n}{n}P_{n}(1-t)^{n}t^{n},t\in[0,1]$

n次贝塞尔曲线可由如下递归表达：

$P_0^{n}=(1-t)P_0^{n-1}+tP_1^{n-1},t\in [0,1]$

————————————————
版权声明：以上内容来自CSDN博主「hailler1119」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/hailler1119/article/details/89195558

4、代码实现

首先来看不同阶数的贝塞尔曲线公式，来找共同点

N = 3: P = (1-t)^2P0 + 2(1-t)tP1 + t^2*P2
N = 4: P = (1-t)^3P0 + 3(1-t)^2tP1 + 3(1-t)t^2P2 + t^3*P3
N = 5: P = (1-t)^4P0 + 4(1-t)^3tP1 + 6(1-t)2*t2P2 + 4(1-t)t^3P3 + t^4*P4

可将贝塞尔曲线一般参数公式中的表达式用如下方式表示：
设有常数 a,b 和 c，则该表达式可统一表示为如下形式：
a * (1 - t)^b * t^c * Pn;

根据上面的分析就可以总结出 a,b,c 对应的取值规则：

b: (N - 1) 递减到 0 (b 为 1-t 的幂)
c: 0 递增到 (N - 1) (c 为 t 的幂)
a: 在 N 分别为 1,2,3,4,5 时将其值用如下形式表示：
N=1:---------1
N=2:--------1 1
N=3:------1 2 1
N=4:-----1 3 3 1
N=5:---1 4 6 4 1
a 值的改变规则为：杨辉三角
-------------------------------------------------------------------

理论基础有了，开始写代码

a 值用杨辉三角计算，b ，c 值在for 循环里计算，Pn从传入的点坐标读取。

step1：首先使用杨辉三角的方式生成a值

N=length(control_points);
ta=zeros(N,N);%%对数组进行初始化
%%杨辉三角左右两边的值赋1% 杨辉三角的数的规律
% 1
% 1 1
% 1 2 1
% 1 3 3 1
% 1 4 6 4 1
for i=1:Nta(i,1)=1;ta(i,i)=1;
end
%%从第二个数开始，也就是从第三行开始，等于前列的左边加上正上方的一个
for row=2:Nfor col=2:rowta(row,col)=ta(row-1,col-1)+ta(row-1,col);end
end

step2：生成贝塞尔曲线上的点

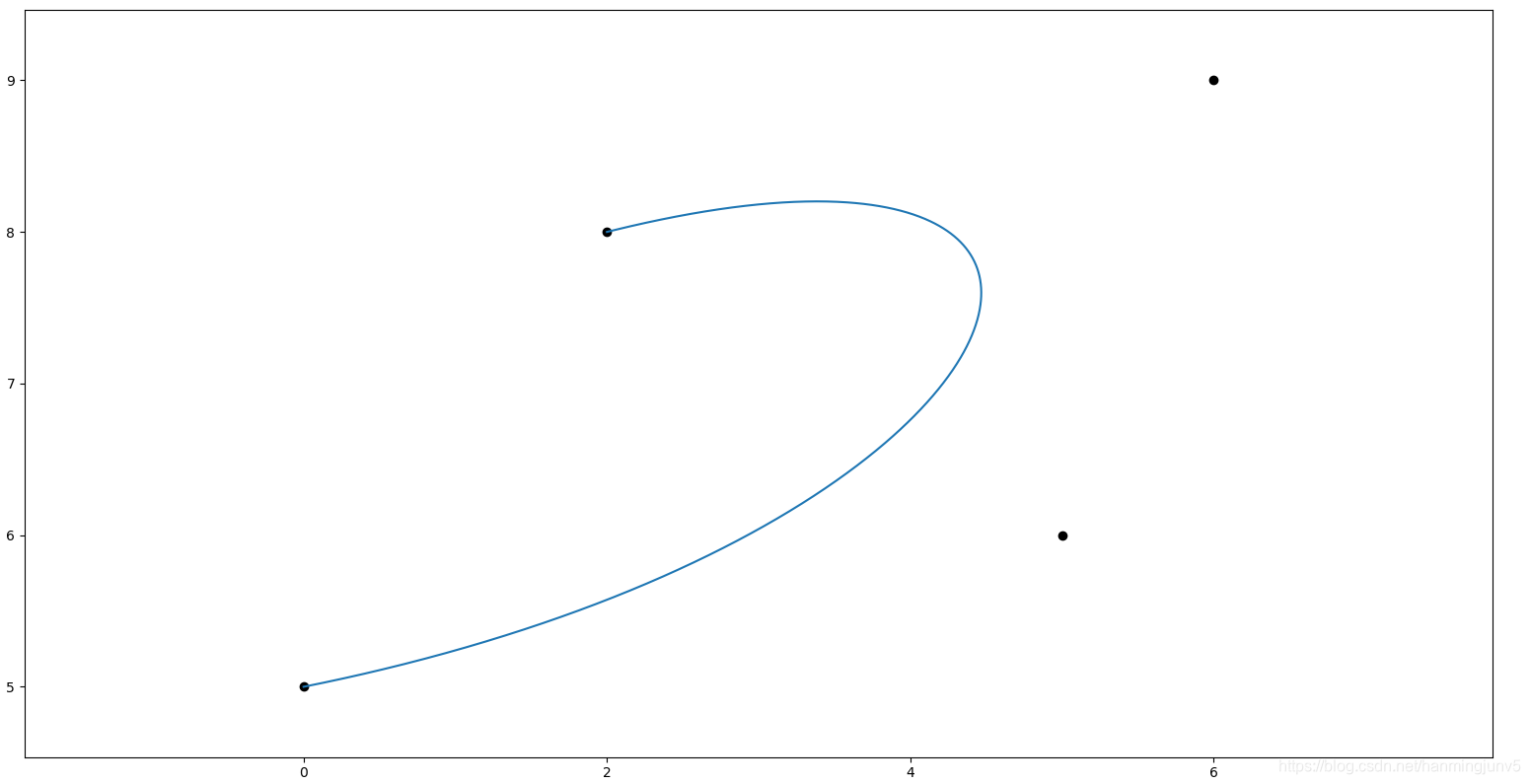
for i=1:Mt=i/M;%%确定每一个点的比例for k=0:N-1c=k;%分别确定a,b,c三个系数b=N-c-1;%分别确定a,b,c三个系数a=ta(N,k+1);%分别确定a,b,c三个系数p(i,1)=p(i,1)+a*(1-t)^b*t^c*control_points(k+1,1);%确定点的x坐标p(i,2)=p(i,2)+a*(1-t)^b*t^c*control_points(k+1,2);%确定点的y坐标endend

下图是一个生成的四阶贝塞尔曲线（有5个控制点）