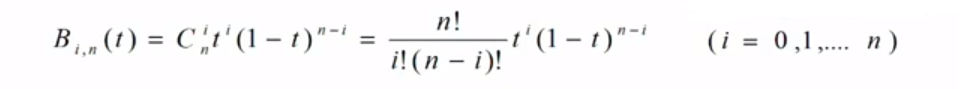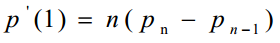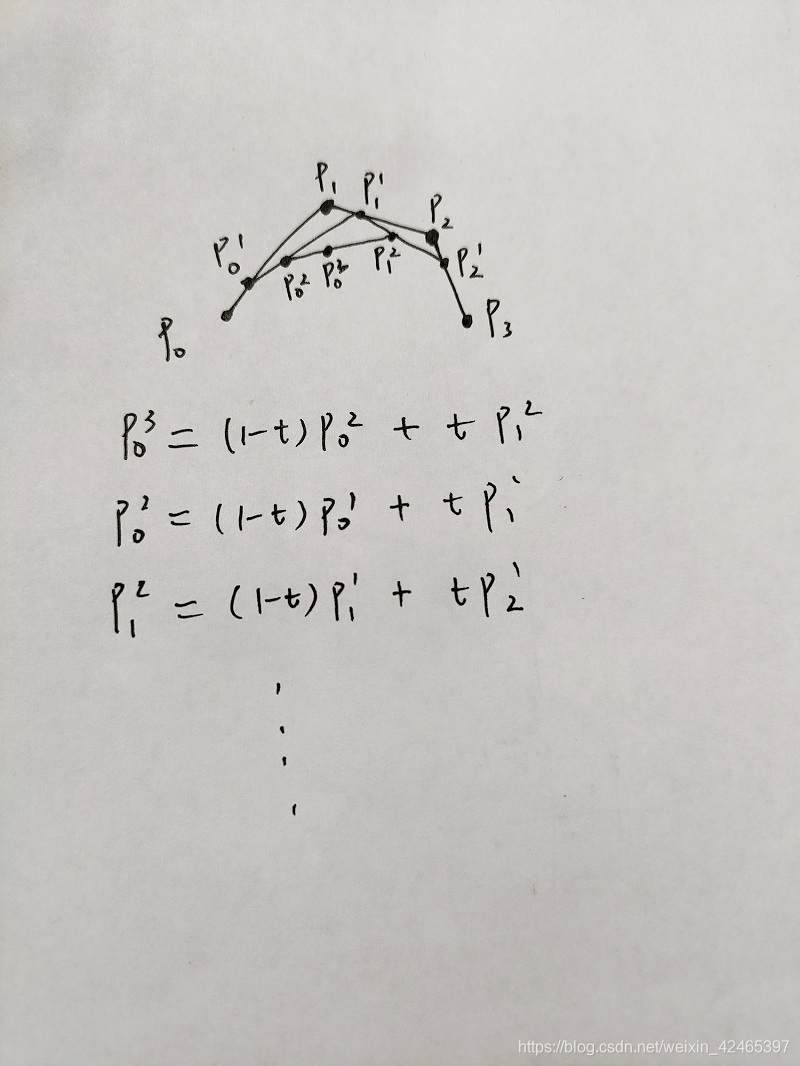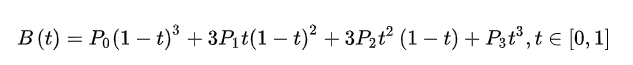原文地址:http://blog.csdn.net/mylovestart/article/details/8434310
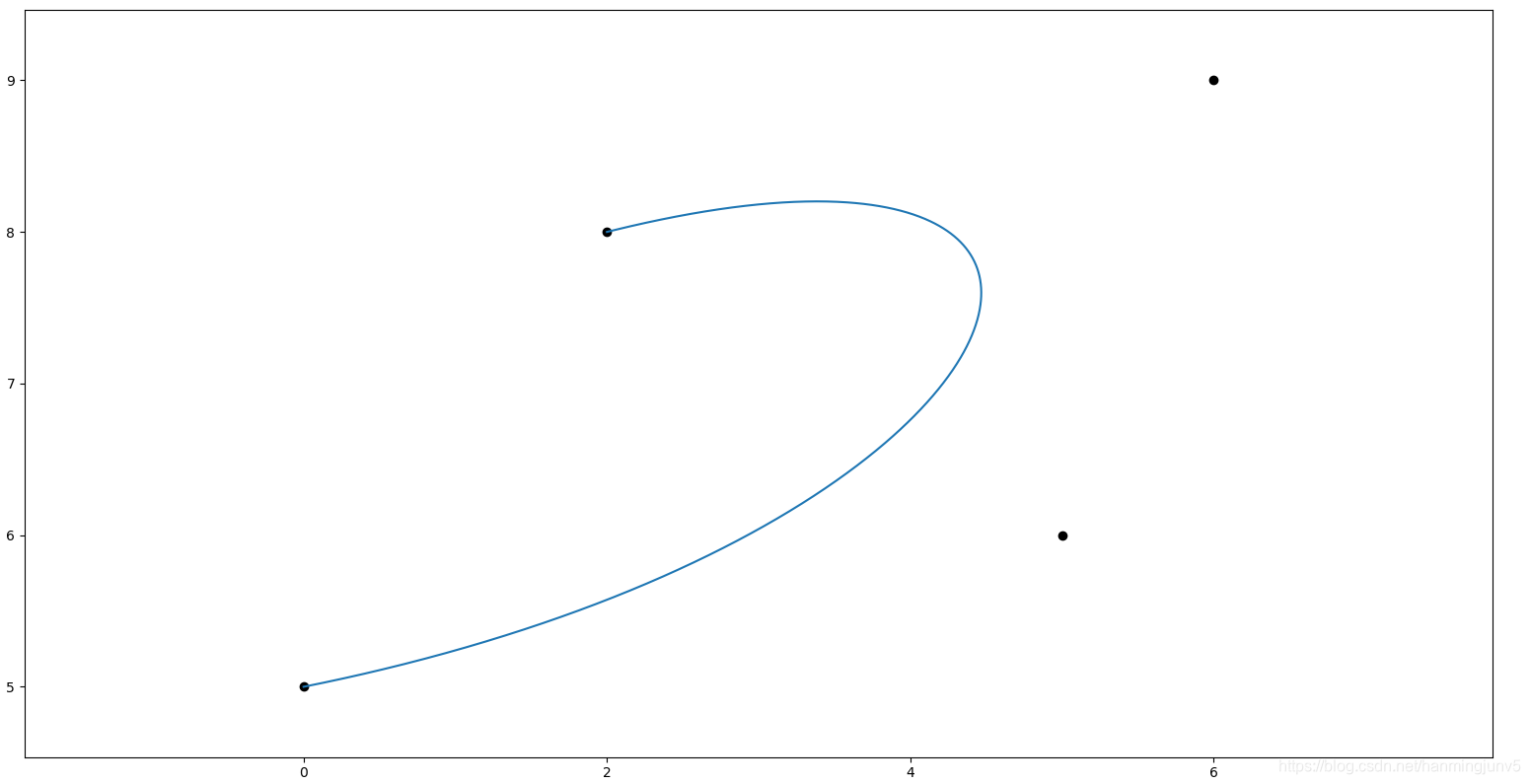
Bezier曲线是参数多项式曲线,它由一组控制多边形折线(控制多边形)的顶点唯一定义,在控制多边形的各顶点中,只有第一个和最后一个顶点在曲线上,其他的顶点则用以定义曲线的导数,阶次和形状
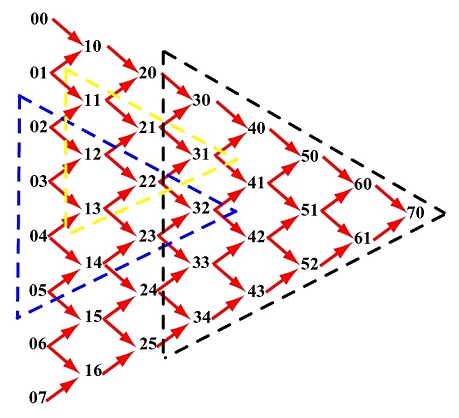
Bezier曲线的数学基础是能够在第一个和最后一个顶点之间进行插值的一个多项式混合函数,对于有n+1个控制点的Bezier曲线段用参数方程表示如下:

式中pk(xk,yk,zk),k=0,1,2…..n是控制多边形的n+1个顶点,BENk,n(t)是Bernstein基函数

下面由键盘输入任意个控制(特征)点,绘制出对应的控制(特征)多边形及Bezier曲线。
先呈上原作者的代码,但是我发现这个代码红色部分写错了,然后我修改了一下,修改后的代码在下面。
#include<stdio.h> #include<string.h> #include<conio.h> #include<windows.h> #include<graphics.h> #include<math.h> #define N 1000 int n;//控制点的个数 struct point //控制点的坐标 { double x; double y; }point[N]; void init() //输入控制点的坐标 { int i; printf("please input the number of the points: "); scanf("%d",&n); printf("please input the location of the points\n"); for(i=0;i<n;i++) scanf("%lf %lf",&point[i].x,&point[i].y); } void sol1() //绘制控制多边形的轮廓 { int i; setcolor(RED); for(i=0;i<n-1;i++) line((int)point[i].x,(int)point[i].y,(int)point[i+1].x,(int)point[i+1].y); }
double sol2(int nn,int k) //计算多项式的系数C(nn,k) { int i; double sum=1; for(i=1;i<=nn;i++) sum*=i; for(i=1;i<=k;i++) sum/=i; for(i=1;i<=nn-k;i++) sum/=i; return sum; } void sol3(double t) //计算Bezier曲线上点的坐标 { double x=0,y=0,Ber; int k; for(k=0;k<n;k++) { Ber=sol2(n-1,k)*pow(t,k)*pow(1-t,n-1-k); x+=point[k].x*Ber; y+=point[k].y*Ber; } putpixel((int)x,(int)y,GREEN); } void sol4() //根据控制点,求曲线上的m个点 { int m=500,i; for(i=0;i<=m;i++) sol3((double)i/(double)m); } int main() { init(); initgraph(640, 480); sol1(); sol4(); getch(); closegraph(); return 0; } #include <stdio.h>
#include <graphics.h>
#include <conio.h>
#include <windows.h>
#include <math.h>
#include <string.h>
#define N 1000
int n;//控制点的个数
struct point//控制点的坐标
{double x;double y;
}point[N];
void init()//输入控制点的坐标、
{int i;printf("请输入点的个数:\n");scanf("%d",&n);printf("请输入控制点的坐标:\n");for(i = 0; i < n; i++){scanf("%lf %lf",&point[i].x,&point[i].y);}
}
void sol1()//绘制控制多边形的轮廓
{int i;setcolor(RED);for(i = 0; i < n - 1; i++){line((int)point[i].x,(int)point[i].y,(int)point[i+1].x,(int)point[i+1].y);}
}
double sol2(int nn,int k)//计算多项式的系数C(nn,k)
{int i;double sum = 1;for(i = nn; i >= k+1; i--){sum *= i;}for(i = nn - k; i >=2; i--){sum /= i;}return sum;
}
void sol3(double t)//计算Bezier曲线上点的坐标
{double x = 0;double y = 0;double Ber;int k;for(k = 0; k< n; k++){Ber = sol2(n-1,k) * pow(t,k) * pow(1-t,n-1-k);x += point[k].x * Ber;y += point[k].y * Ber;}putpixel((int)x,(int)y,GREEN);
}
void sol4()//根据控制点,求曲线上的m个点
{int i;int m = 5000;for(i = 0; i <= m; i++){sol3((double)i / (double)m);}
}
int main()
{init();initgraph(1640,1480);sol1();sol4();getch();closegraph();return 0;
}
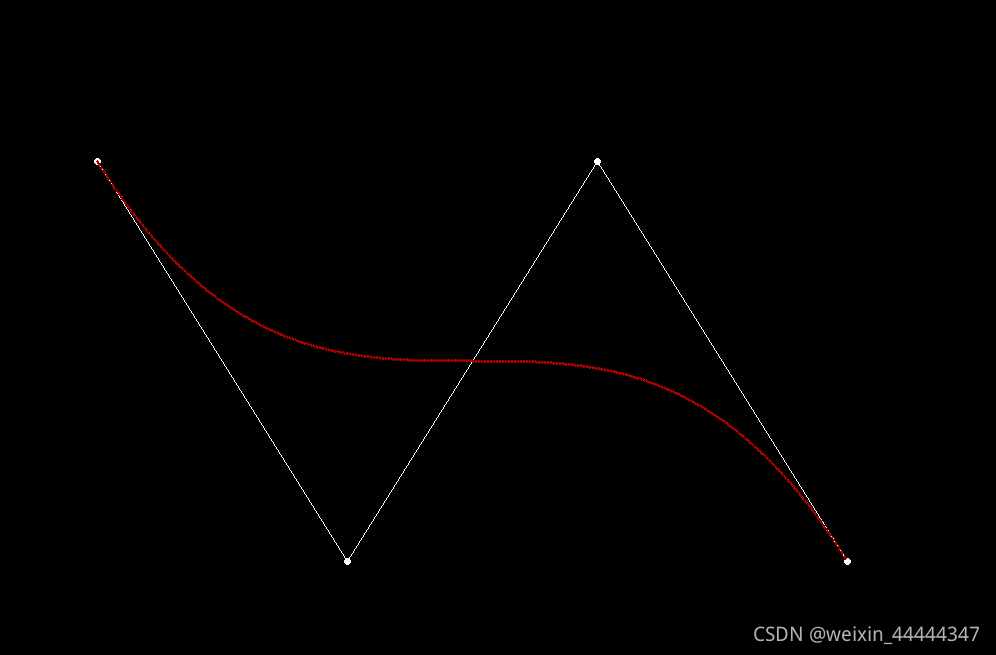
最后附上截图