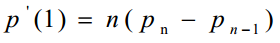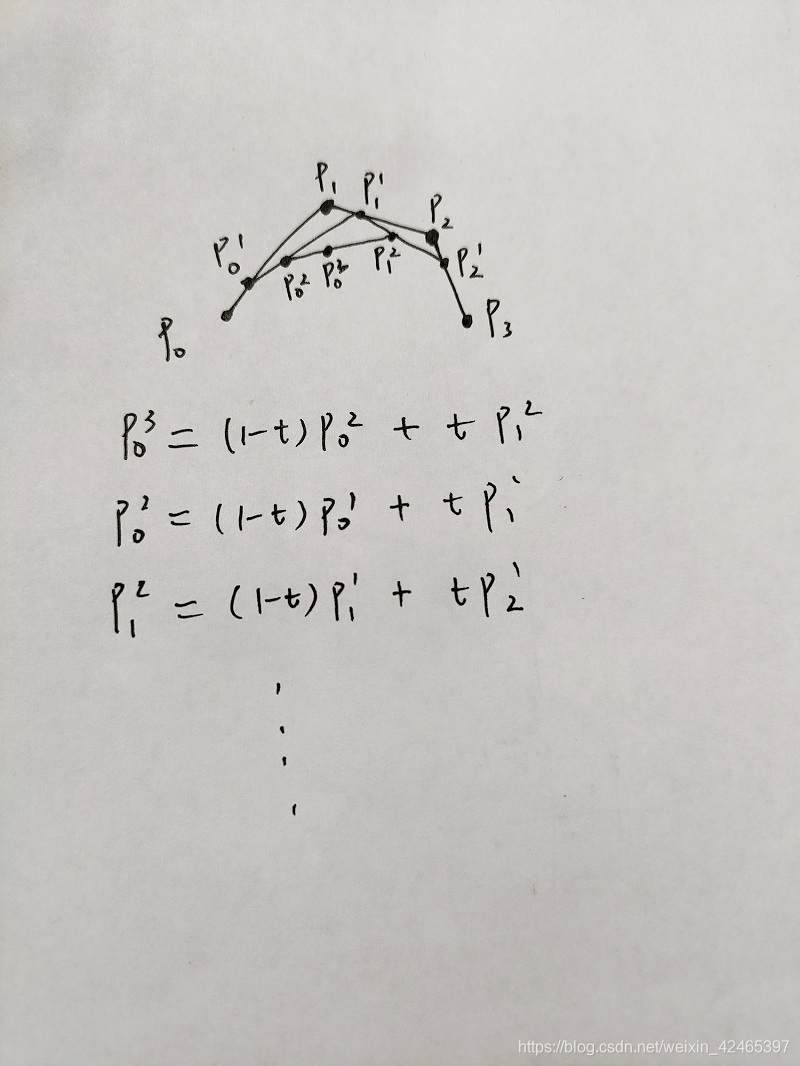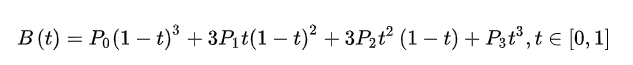根据Bezier曲线的定义公式实现Bezier曲线的绘制

article/2025/11/9 18:10:10

Bezier曲线的定义公式

在这里插入图片描述
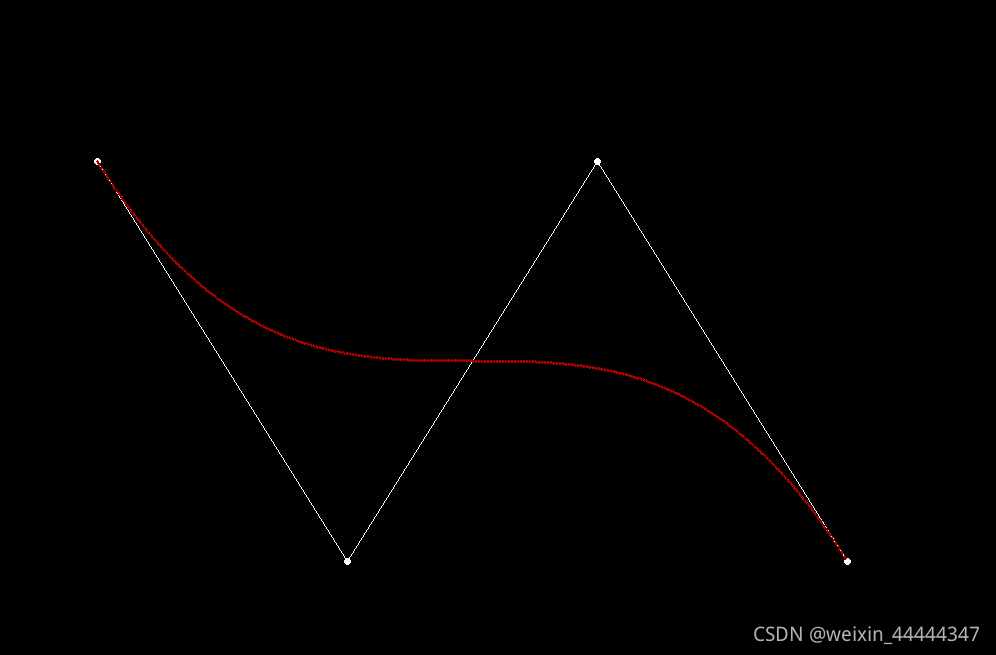
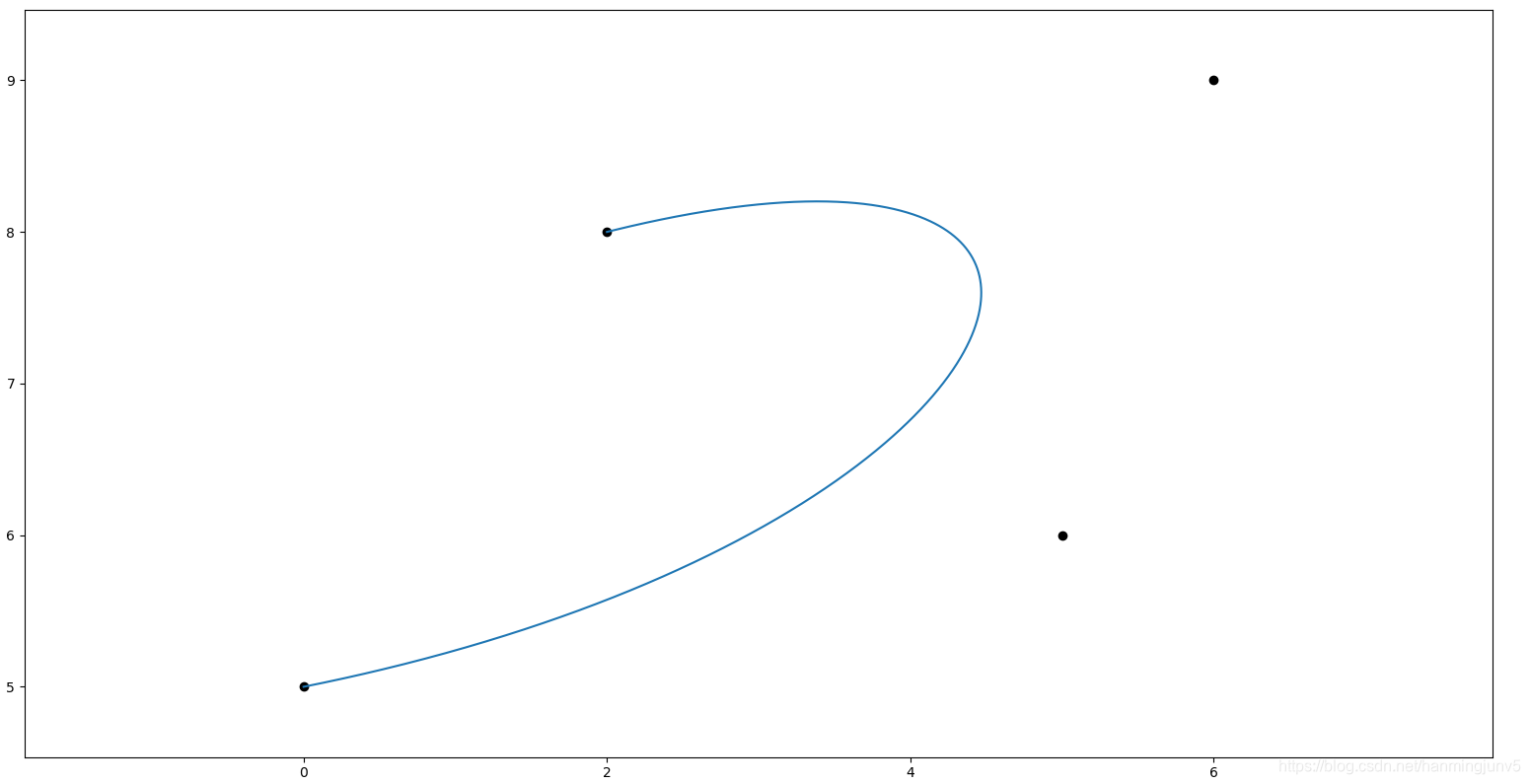
P_i是曲线上点的坐标（x,y,(z=0)）， B_i,n(t)伯恩斯坦公式，绘制Bezier曲线的第一种方法是根据这个公式来绘制。首先看看绘制的效果：

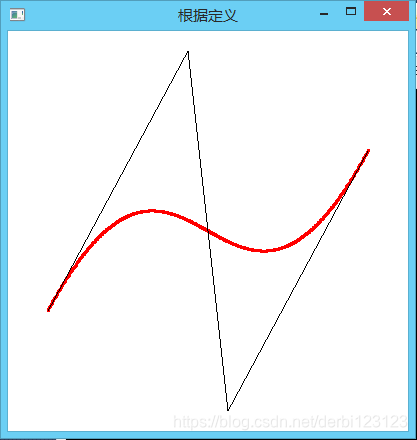
（1）计算定义中多项式的值

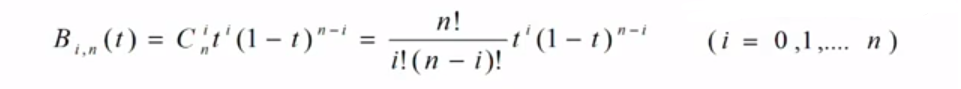
在这里插入图片描述
首先要求伯恩斯坦公式的多项式的值C_nⁱ，写成后面这种阶乘的形式方便用程序去表达了：

//计算定义中多项式的值
void GetCnk(GLint n,GLint *c)//n是控制点的个数，C用来存多项式值的数组
{GLint i,j;for(j=0;j<n;j++){//循环前先从n!中把i!消掉，注意体会c[j]=1;for(i=n-1;i>=j+1;i--)c[j]=c[j]*i;for(i=n-1-j;i>=2;i--)c[j]=c[j]/i;}
}

（2）计算曲线上点的坐标

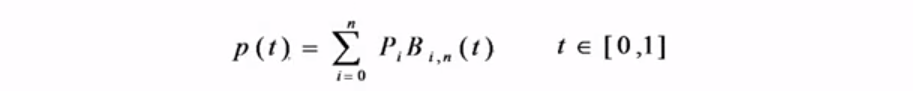
在这里插入图片描述
P_i是曲线上点的坐标（x,y,(z=0)），所以我们可以把p(t)表示成三个坐标分量的形式：

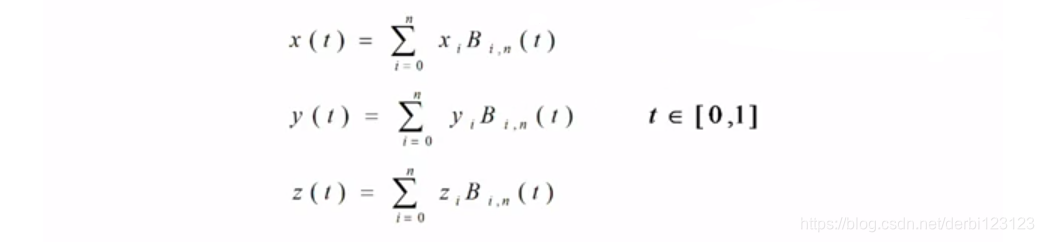
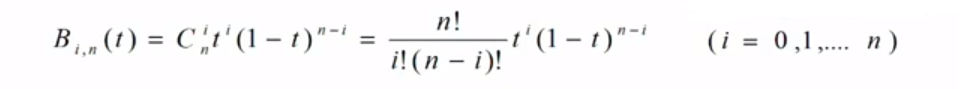
//计算曲线上点的坐标
void GetPointPr(GLint *c,GLfloat t,Pt3D *Pt,GLint ControlN,Pt3D *ControlP)
{//c是存多项式值的数组,t是参数值，Pt是曲线上某点坐标，ControlN是控制点个数，ControlP是控制点坐标GLint i,n=ControlN;GLfloat Berstein;Pt->x=0.0;Pt->y=0.0;Pt->z=0.0;for(i=0;i<ControlN;i++){Berstein=c[i]*pow(t,i)*pow(1-t,n-1-i);Pt->x+=ControlP[i].x*Berstein;Pt->y+=ControlP[i].y*Berstein;Pt->z+=ControlP[i].z*Berstein;}
}

（3）根据求出的坐标绘制Bezier曲线

void Bezierdraw(GLint m,GLint ControlN,Pt3D *ControlP)
{//m是曲线上点的个数，ControlN是控制点个数，ControlP是控制点坐标GLint *C,i;Pt3D CurvePt;//保存当前点坐标C=new GLint[ControlN];//存多项式系数的数组CGetCnk(ControlN,C);glColor3f(1.0,0.0,0.0);glPointSize(3);//曲线画粗点和控制图形区分glBegin(GL_POINTS);for(i=0;i<=m;i++){GetPointPr(C,(GLfloat)i/m,&CurvePt,ControlN,ControlP);glVertex2f(CurvePt.x,CurvePt.y);}glEnd();delete [] C;
}

总的代码：

#include <GL/freeglut.h>
#include <math.h>
class Pt3D{public:GLfloat x,y,z;
};//坐标类//计算定义中多项式的值
void GetCnk(GLint n,GLint *c)//n是控制点的个数，C用来存多项式值的数组
{GLint i,j;for(j=0;j<n;j++){//循环前先从n!中把i!消掉，注意体会c[j]=1;for(i=n-1;i>=j+1;i--)c[j]=c[j]*i;for(i=n-1-j;i>=2;i--)c[j]=c[j]/i;}
}//计算曲线上点的坐标
void GetPointPr(GLint *c,GLfloat t,Pt3D *Pt,GLint ControlN,Pt3D *ControlP)
{//c是存多项式值的数组,t是参数值，Pt是曲线上某点坐标，ControlN是控制点个数，ControlP是控制点坐标GLint i,n=ControlN;GLfloat Berstein;Pt->x=0.0;Pt->y=0.0;Pt->z=0.0;for(i=0;i<ControlN;i++){Berstein=c[i]*pow(t,i)*pow(1-t,n-1-i);Pt->x+=ControlP[i].x*Berstein;Pt->y+=ControlP[i].y*Berstein;Pt->z+=ControlP[i].z*Berstein;}
}//根据控制点，画曲线上的500个点
void Bezierdraw(GLint m,GLint ControlN,Pt3D *ControlP)
{//m是曲线上点的个数，ControlN是控制点个数，ControlP是控制点坐标GLint *C,i;Pt3D CurvePt;//保存当前点坐标C=new GLint[ControlN];//存多项式系数的数组CGetCnk(ControlN,C);glColor3f(1.0,0.0,0.0);glPointSize(3);//曲线画粗点和控制图形区分glBegin(GL_POINTS);for(i=0;i<=m;i++){GetPointPr(C,(GLfloat)i/m,&CurvePt,ControlN,ControlP);glVertex2f(CurvePt.x,CurvePt.y);}glEnd();delete [] C;
}
void myinit(void)
{glClearColor(1.0f,1.0f,1.0f,1.0f);
}
//窗口大小变化时的回调函数
void myReshape(GLsizei w, GLsizei h)
{//设定视区glViewport(0, 0, w, h);//设定透视方式glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(-100.0,100.0,-100.0,100.0);
}
void display(void)
{//设置清除屏幕的颜色，并清除屏幕glClear(GL_COLOR_BUFFER_BIT);GLint ControlN=4;//4个控制点GLint m=500;//曲线由500个点绘制而成Pt3D ControlP[4]={{-80.0,-40.0,0.0},{-10.0,90.0,0.0},{10.0,-90.0,0.0},{80.0,40.0,0.0}};//控制点坐标//画曲线Bezierdraw(m,ControlN,ControlP);//画控制图形glColor3f(0.0,0.0,0.0);glBegin(GL_LINE_STRIP);for(int i=0;i<ControlN;i++){glVertex3f(ControlP[i].x,ControlP[i].y,ControlP[i].z);}glEnd();//交换前后缓冲区glutSwapBuffers();
}
int main(int argc, char* argv[])
{glutInit(&argc, argv);//根据定义//初始化OPENGL显示方式glutInitDisplayMode (GLUT_DOUBLE | GLUT_RGBA);//设定OPENGL窗口位置和大小glutInitWindowSize (400, 400); glutInitWindowPosition (100, 100);//打开窗口glutCreateWindow ("根据定义");//调用初始化函数myinit();//设定窗口大小变化的回调函数glutReshapeFunc(myReshape);//开始OPENGL的循环glutDisplayFunc(display); glutMainLoop();return 0;
}