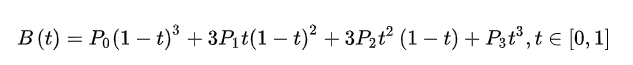Bezier曲线构造
曲线公式
曲 线 : C ( u ) = ∑ i = 0 n B n , i ( u ) P i 基 函 数 : B n , i = n ! i ! ( n − i ) ! u i ( 1 − u ) n − i 曲线:C(u) = \sum^n_{i=0}B_{n,i}(u)P_i\\ 基函数:B_{n,i}=\frac{n!}{i!(n-i)!}u^i(1-u)^{n-i} 曲线:C(u)=i=0∑nBn,i(u)Pi基函数:Bn,i=i!(n−i)!n!ui(1−u)n−i
曲线性质
1.Bezir曲线的阶数由控制点个数决定,n+1个控制点,则对应阶数为n. 例如3次Bezir曲线需要4个点,2次Bezir曲线需要3个点.
2.Bezir曲线通过第一个点和最后一个点.
3.所有的样条基函数均为非负数.
4.Bezir曲线完全位于给定的n+1个控制点的凸包内
5.仿射不变性
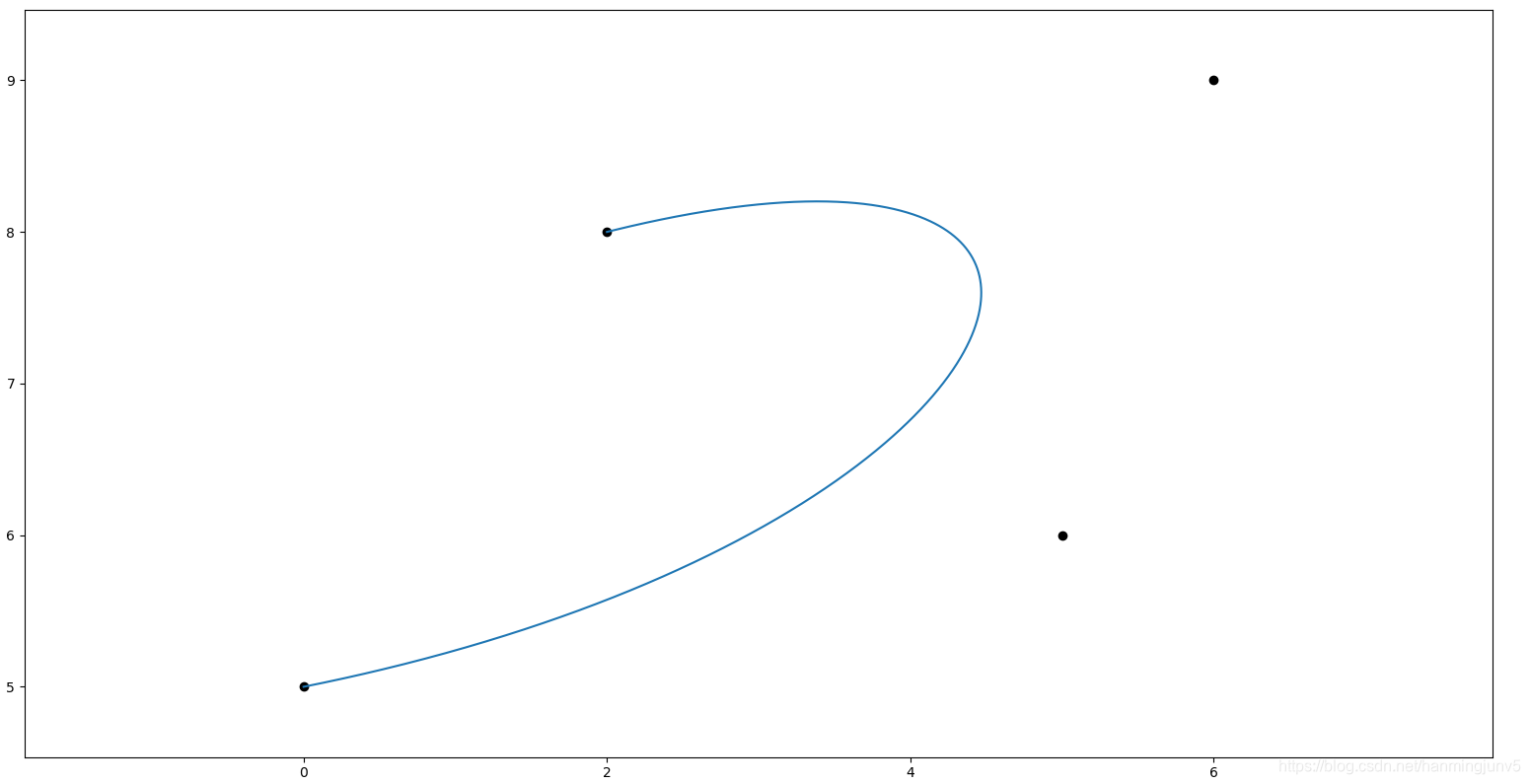
三次Bezier曲线
三次Bezier曲线是最常用的曲线,这里注重讲一下。
由曲线公式可得:
C ( u ) = ∑ i = 0 3 B 3 , i ( u ) P i = ( 1 − u ) 3 P 0 + 3 ( 1 − u ) 2 u P 1 + 3 ( 1 − u ) u 2 P 2 + u 3 P 3 , 0 ≤ u ≤ 1 C(u) = \sum^3_{i=0}B_{3,i}(u)P_i=(1-u)^3P_0+3(1-u)^2uP_1+3(1-u)u^2P_2+u^3P_3,\quad 0\le u \le 1 C(u)=i=0∑3B3,i(u)Pi=(1−u)3P0+3(1−u)2uP1+3(1−u)u2P2+u3P3,0≤u≤1
设:
J 3 , 0 ( u ) = ( 1 − u ) 3 = 1 ( 1 − u ) 3 u 0 J 3 , 1 ( u ) = 3 ( 1 − u ) 2 u = 3 ( 1 − u ) 2 u 1 J 3 , 2 ( u ) = 3 ( 1 − u ) u 3 = 3 ( 1 − u ) 1 u 2 J 3 , 3 ( u ) = u 3 = 1 ( 1 − u ) 0 u 3 C ( u ) = J 3 , 0 P 0 + J 3 , 1 P 1 + J 3 , 2 P 2 + J 3 , 3 P 3 \begin {aligned} J_{3,0}(u)&=(1-u)^3&=1(1-u)^3u^0\\ J_{3,1}(u)&=3(1-u)^2u&=3(1-u)^2u^1\\ J_{3,2}(u)&=3(1-u)u^3&=3(1-u)^1u^2\\ J_{3,3}(u)&=u^3&=1(1-u)^0u^3\\ C(u)&=J_{3,0}P_0+J_{3,1}P_1+J_{3,2}P_2+J_{3,3}P_3 \end {aligned} J3,0(u)J3,1(u)J3,2(u)J3,3(u)C(u)=(1−u)3=3(1−u)2u=3(1−u)u3=u3=J3,0P0+J3,1P1+J3,2P2+J3,3P3=1(1−u)3u0=3(1−u)2u1=3(1−u)1u2=1(1−u)0u3
部分性质
u=0 u=1处的值:
J 3 , 0 ( 0 ) = 1 J 3 , 0 ( 1 ) = 0 J 3 , 1 ( 0 ) = 0 J 3 , 1 ( 1 ) = 0 J 3 , 2 ( 0 ) = 0 J 3 , 2 ( 1 ) = 0 J 3 , 3 ( 0 ) = 0 J 3 , 3 ( 1 ) = 1 \begin {aligned} J_{3,0}(0)&=1\quad J_{3,0}(1)&=0\\ J_{3,1}(0)&=0\quad J_{3,1}(1)&=0\\ J_{3,2}(0)&=0\quad J_{3,2}(1)&=0\\ J_{3,3}(0)&=0\quad J_{3,3}(1)&=1\\ \end {aligned} J3,0(0)J3,1(0)J3,2(0)J3,3(0)=1J3,0(1)=0J3,1(1)=0J3,2(1)=0J3,3(1)=0=0=0=1
基函数和:
J 3 , 0 ( u ) + J 3 , 1 ( u ) + J 3 , 2 ( u ) + J 3 , 3 ( u ) = 1 , 0 ≤ u ≤ 1 J_{3,0}(u)+J_{3,1}(u)+J_{3,2}(u)+J_{3,3}(u)=1,0\le u \le1 J3,0(u)+J3,1(u)+J3,2(u)+J3,3(u)=1,0≤u≤1
基函数一次导数:
J 3 , 0 ′ ( 0 ) = − 3 J 3 , 0 ′ ( 1 ) = 0 J 3 , 1 ′ ( 0 ) = 3 J 3 , 1 ′ ( 1 ) = 0 J 3 , 2 ′ ( 0 ) = 0 J 3 , 2 ′ ( 1 ) = − 3 J 3 , 3 ′ ( 0 ) = 0 J 3 , 3 ′ ( 1 ) = 3 \begin {aligned} J^{'}_{3,0}(0)&=-3\quad &J^{'}_{3,0}(1)=0\\ J^{'}_{3,1}(0)&=3\quad &J^{'}_{3,1}(1)=0\\ J^{'}_{3,2}(0)&=0\quad &J^{'}_{3,2}(1)=-3\\ J^{'}_{3,3}(0)&=0\quad &J^{'}_{3,3}(1)=3\\ \end {aligned} J3,0′(0)J3,1′(0)J3,2′(0)J3,3′(0)=−3=3=0=0J3,0′(1)=0J3,1′(1)=0J3,2′(1)=−3J3,3′(1)=3
基函数一次导数:
J 3 , 0 ′ ′ ( 0 ) = 6 J 3 , 0 ′ ′ ( 1 ) = 0 J 3 , 1 ′ ′ ( 0 ) = − 12 J 3 , 1 ′ ′ ( 1 ) = 0 J 3 , 2 ′ ′ ( 0 ) = 0 J 3 , 2 ′ ′ ( 1 ) = − 12 J 3 , 3 ′ ′ ( 0 ) = 0 J 3 , 3 ′ ′ ( 1 ) = 6 \begin {aligned} J^{''}_{3,0}(0)&=6\quad &J^{''}_{3,0}(1)=0\\ J^{''}_{3,1}(0)&=-12\quad &J^{''}_{3,1}(1)=0\\ J^{''}_{3,2}(0)&=0\quad &J^{''}_{3,2}(1)=-12\\ J^{''}_{3,3}(0)&=0\quad &J^{''}_{3,3}(1)=6\\ \end {aligned} J3,0′′(0)J3,1′′(0)J3,2′′(0)J3,3′′(0)=6=−12=0=0J3,0′′(1)=0J3,1′′(1)=0J3,2′′(1)=−12J3,3′′(1)=6
基函数最大值:
基 函 数 最 大 值 出 现 在 : J 3 , k ( u ) , u = k 3 , k = 0 , 1 , 2 , 3 基函数最大值出现在:J_{3,k}(u),u = \frac{k}{3},k=0,1,2,3 基函数最大值出现在:J3,k(u),u=3k,k=0,1,2,3