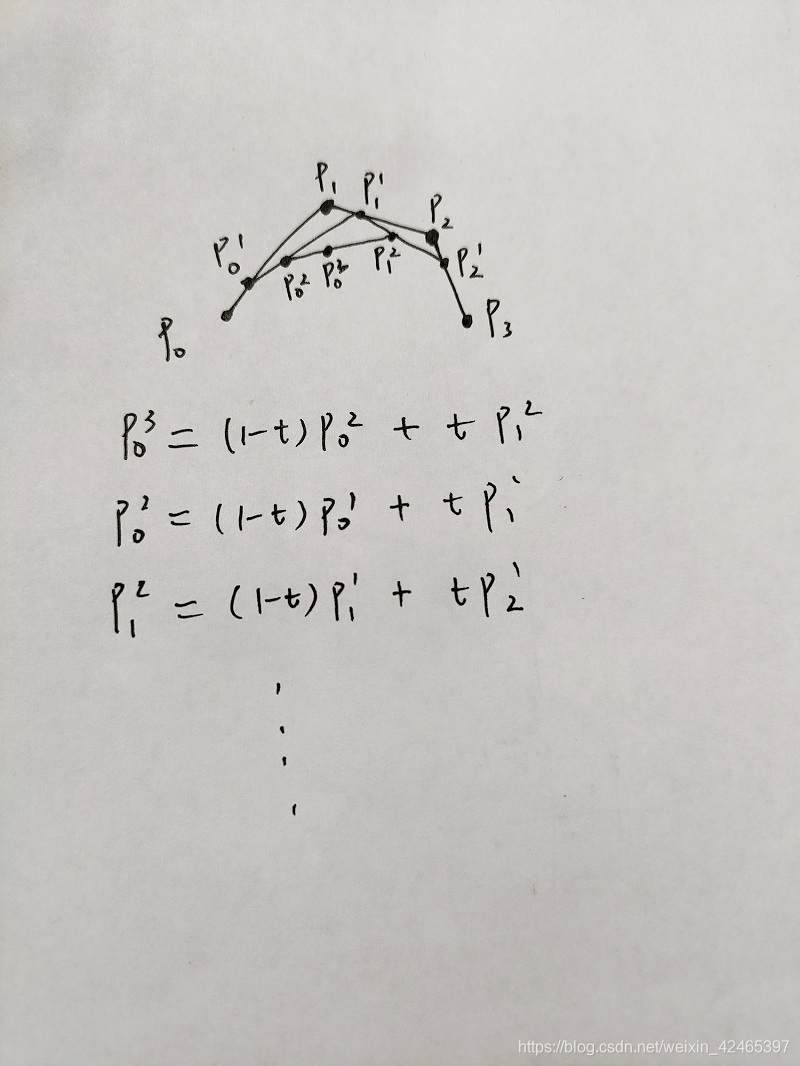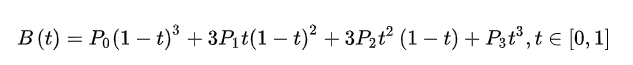Bezier曲线

1.Bezier曲线的定义

当用曲线段拟合曲线f(x)时，可以把曲线表示为许多小线段φi(x)之和，其中φi(x)称为基（混合）函数。

                                 

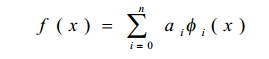
这些基（混合）函数是要用于计算和显示的。因此，经常选择多项式作为基（混合）函数，即：    

                                   

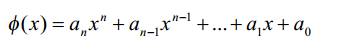
贝塞尔把参数n次曲线表示为：
 

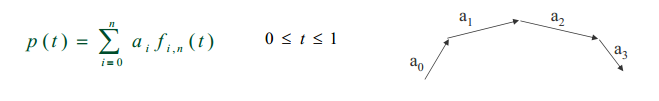
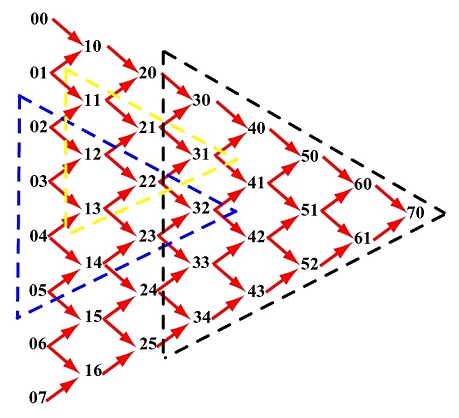
系数矢量（i=0,1,…,n）顺序首位相接，决定了从的轨迹。

比如在n = 1的条件下，,当t = 0时，p(0) = ,当然，t = 1时，p(1) =  。

那么在n = 2 的条件下，也会出现：当t = 0时，p(0) = ，t = 1时，p(1) =  ，只是轨迹不同。

那么那个决定轨迹的函数的形式是什么？

 

2.Bezier基函数的导出

Forest证明了Bezier曲线的基函数可以简化成伯恩斯坦基函数！

那么伯恩斯但基函数是啥？

伯恩斯但基函数：

一个连续函数 y=f（x），任给一个ξ＞0，总能找到一个多项式和这个函数足够逼近。逼近的形式是：

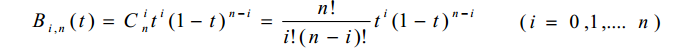
表示从n个不同元素中，任取i(i≤n)个元素并成一组，叫做从n个不同元素中取出i个元素的一个组合，

其实：

3.重新定义Bezier曲线

针对Bezier曲线，给定空间n+1个点的位置矢量Pi（i=0，1，2，…，n），则Bezier曲线段的参数方程表示如下                                                      
                                                        

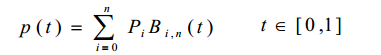
其中pi（xi,yi,zi）,i=0,1,2…n 是控制多边形的n+1个顶点，即构成该曲线的特征多边形；是Bernstein
基函数。

Pi代表空间的很多点，t在0到1之间，把t代进去可以算出一个数--即平面或空间一个点随着t值的变化，点也在变化。当t从0变到1时，就得到空间的一个图形，这个图形就是bezier曲线。

4.Bezier曲线的举例

1）一次Bezier曲线

将n = 1带入上述式子，得到：

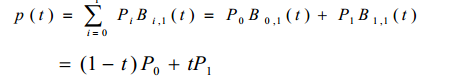
画图为：

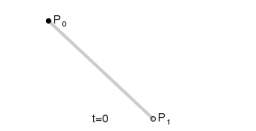  实质就是连接P0与P1的直线段

2）二次Bezier曲线

             

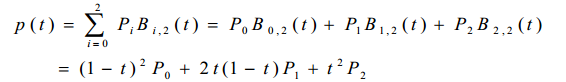
矩阵形式为：

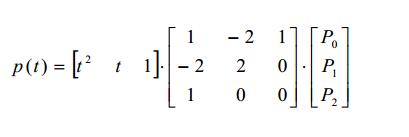图形为：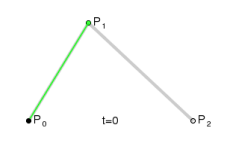

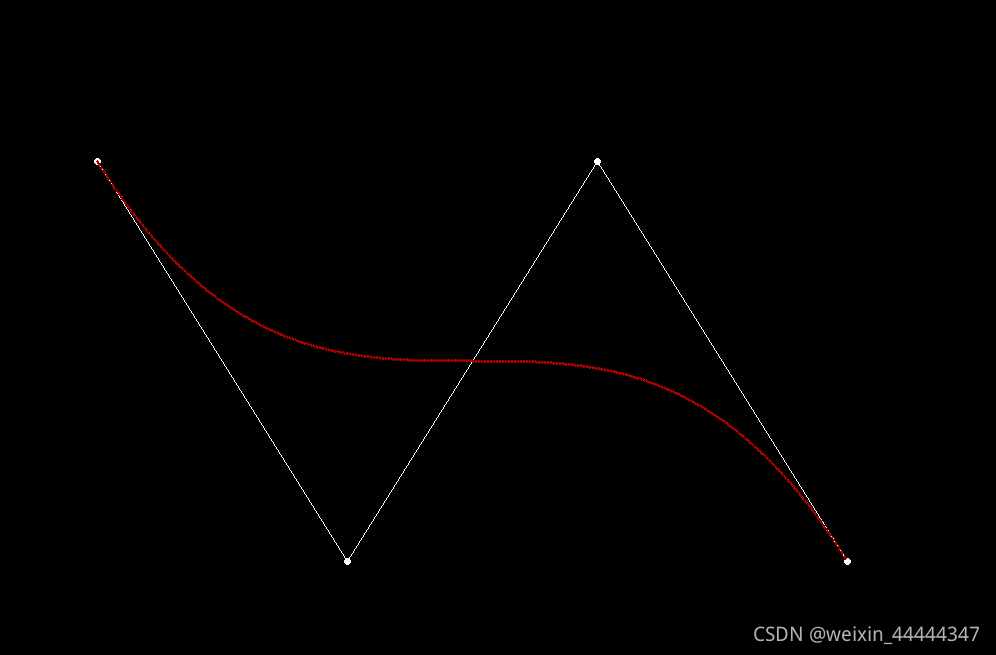
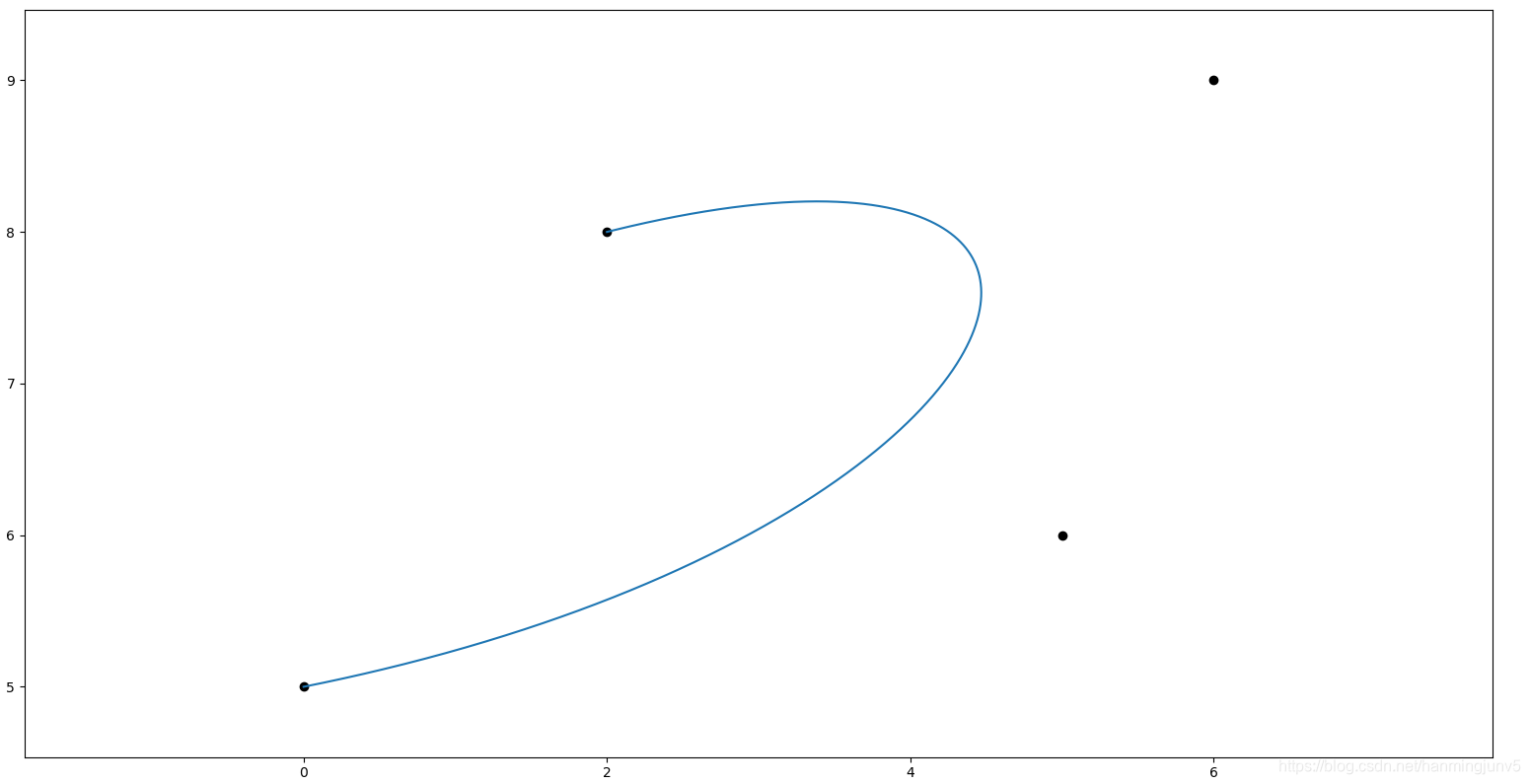
3）三次Bezier曲线

            

故三次Bezier曲线的图形为的线性组合。

矩阵形式：

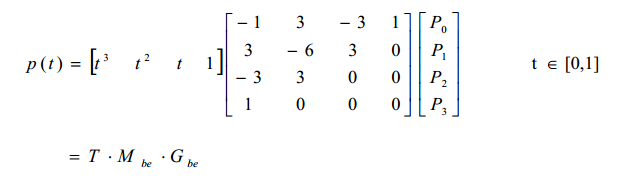
其中，Mbe是三次Bezier曲线系数矩阵，为常数；Gbe是4个控制点位置矢量。
 

5.Bernstein基函数的性质

基函数形式为：

                 

其实这些性质都是的性质

1）非负性

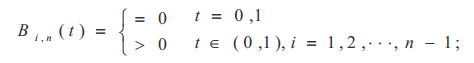
2）权性：

 基函数有n+1项，n+1个基函数的和加起来正好等于1。

origin from（因为）：

3）端点性质：

                                 

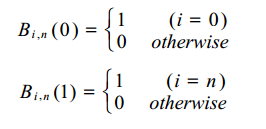
4）对称性

假如保持n次Bezier曲线控制多边形的顶点位置不变，而把次序颠倒过来，则此时曲线仍不变，只不过曲线
的走向相反而已
 

5）递推性

                

即n次的Bernstein基函数可由两个n-1次的Bernstein基函数线性组合而成。因为：
                                      

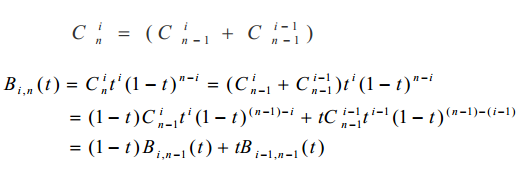
6）导函数

                      

7）最大值

                  

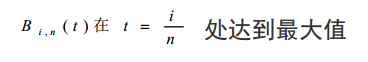
8）积分

                      

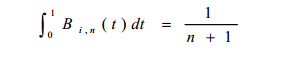
9)降阶公式

            

10)升阶公式

                       

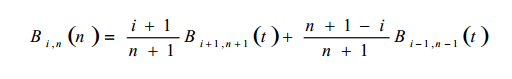
6.Bernstein曲线的性质
 

1)端点性质

顶点p0和pn分别位于实际曲线段的起点和终点上。即p(0)（函数值） = (点),        p(1)  =

2)一阶导数

              

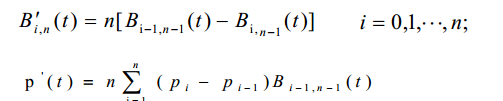
当t = 0 时：

当t = 1时：

这说明Bezier曲线的起点和终点处的切线方向和特征多边形的第一条边及最后一条边的走向一致
 

3）几何不变性

Bezier曲线的形状仅与控制多边形各顶点的相对位置有关，而与坐标系的的选择无关

4）变差缩减性

若Bezier曲线的特征多边形是一个平面图形，则平面内任意直线与p(t)的交点个数不多于该直线与其特征多边
形的交点个数，这一性质叫变差缩减性质