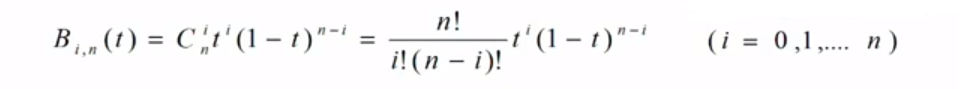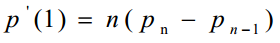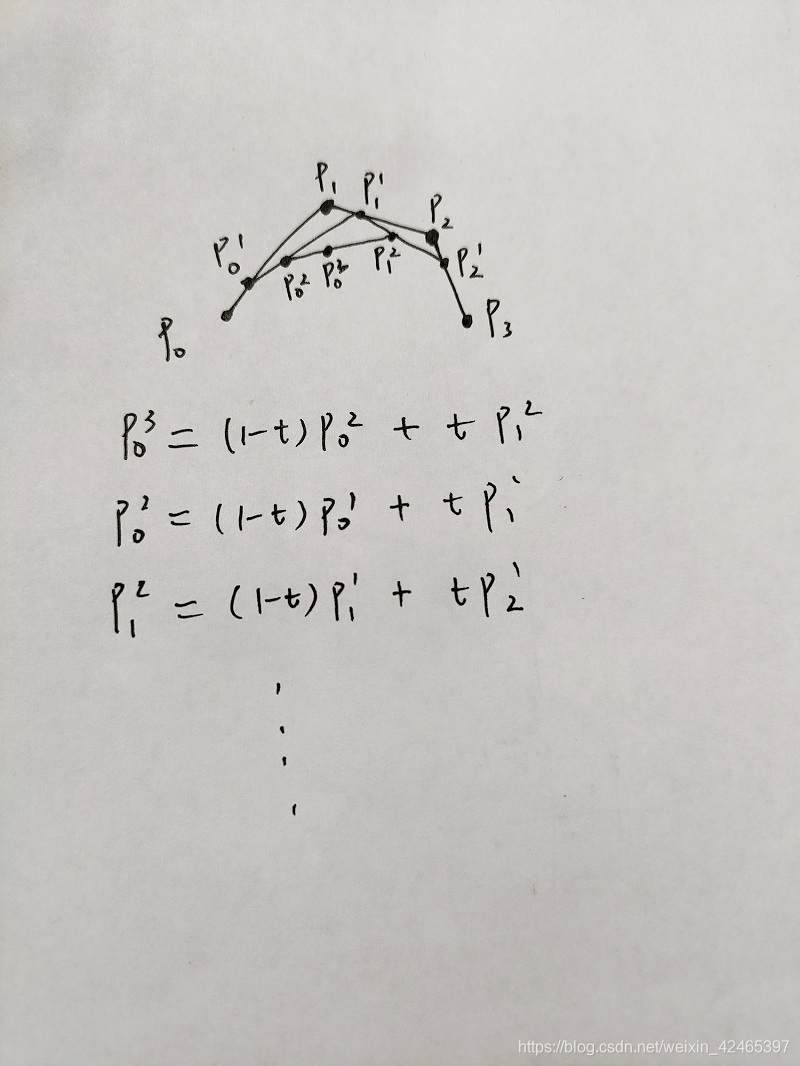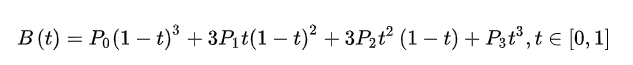在初学时，我发现Bezier曲线（中文名贝塞尔曲线，想要了解历史发展等的可以看此百度百科：贝塞尔曲线_百度百科）很难理解，故在此写了一篇自己的心得感悟。要理解它最重要的是理解Bernstein基函数。首先，书上边的定义应理解为：对于有n+1个控制点（n至少为1且必须是整数）的n次贝塞尔曲线（三次最为常用因为是自由曲线且相对于多次没那么复杂），其矢量表示为

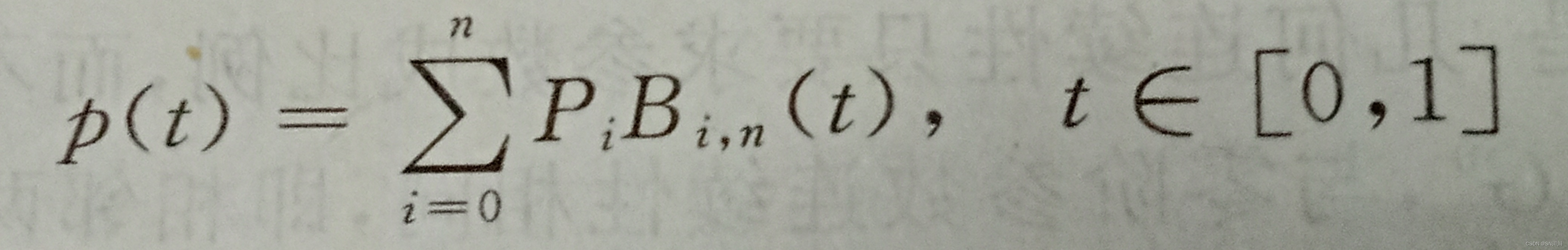
 这儿Pi就是值的编号为0-n的控制点，后面紧跟基函数。每个贝塞尔曲线均可以用此矢量公式来表示（方便转为矩阵表示）。现在我们来分析基函数（我的教材孔令德编著的计算机图形学基础教程第二版）。

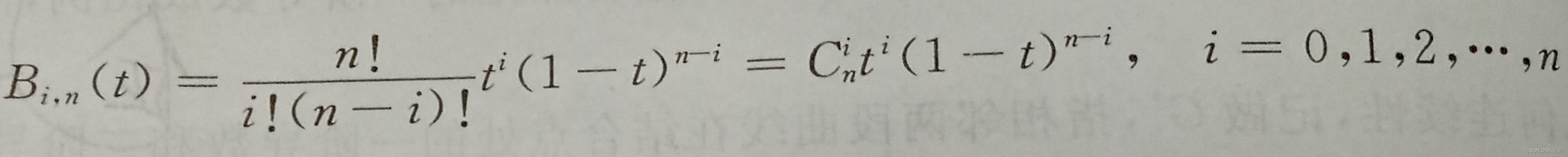
 首先我们要搞懂贝塞尔曲线的本质和什么是矢量方程（书上都没说）。对此可以参考这篇博客了解贝塞尔曲线的基础贝塞尔曲线简单介绍_xiaozhang2019的博客-CSDN博客_贝塞尔曲线 ，写的很好。大概就是说第一条任选中间一点然后每条条按照相同的比例选点，各点连接再按此比例，所形成的点的集合就是我们贝塞尔曲线的点集，在一些题目中如果我们不想用公式性质其实可以用这个来解题。然后，什么是矢量方程？在平面坐标系中，矢量方程中指的矢量就是原点连接我们曲线上的一点所形成的矢量的方程，而在参数方程中，每一个参数t对应一个x，y坐标，对应一个矢量，所以就有了矢量参数方程（分为x和y的部分，不同分开写，相同可以合并写表示矢量）。因此其实矢量方程和我们曲线的点方程是很相似的，它的好处就是方便写出矩阵形式（矩阵形式就是把参数矢量方程写成矩阵相乘而已本质一样）且简洁。

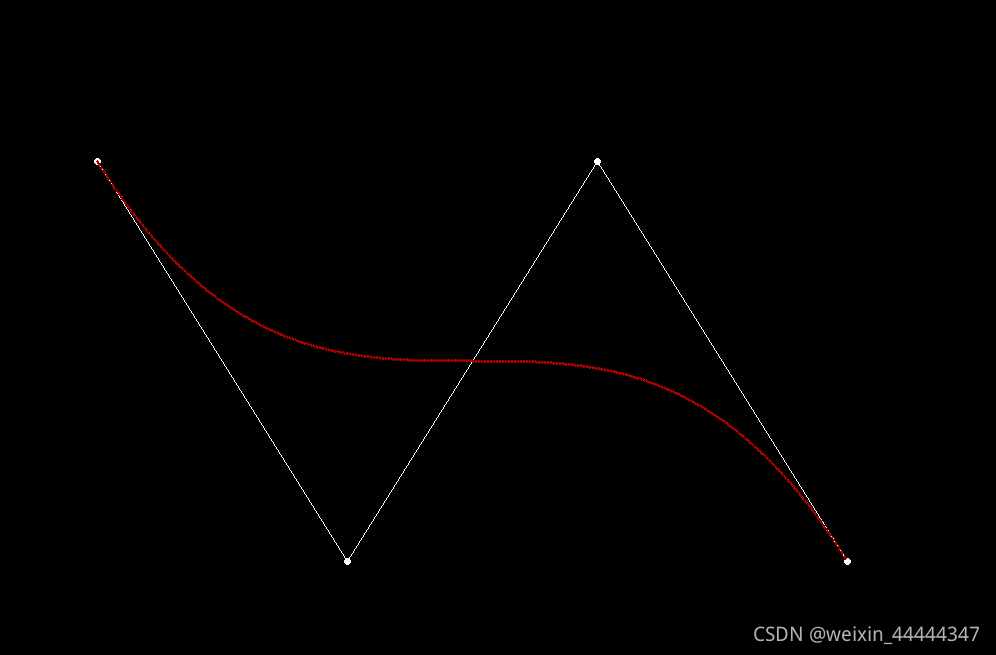
然后看基函数公式，t要在0到1的闭区间之间，原因是我们把公式展开，会发现t的值代表的就是我们贝塞尔曲线上的矢量的位置，t=0必定是起点P0，t=1必定是终点P1（所以基函数具有非负性），所以t的范围为0到1。反之带入不同的参数，用P0，P1作为基准点就可以画出曲线（初学分析时P0，P1可各看成矢量，矢量相加到曲线上点与原点的矢量，也可作出图）。另外基函数本身是分别对应各个点（P0的基函数，P1...），n次贝塞尔曲线就有n各基函数，与点矢量各自相乘再相加就得到整体的公式，代入t画矢量得到曲线点。到这儿就应该真正理解了。

最后根据公式代入特殊值或展开以及展开后按t的变化画的曲线就可以得到贝塞尔曲线的各种性质。前面理解了这儿就相对容易，这儿我挑几个不好理解的地方讲。

基函数的权性：所有基函数的和恒等于1。

基函数的下标：下标i，n应该看成是一个整体，而不局限与i，n，比如n-i-1,n-1，n-i是指从n-1开始到0的基函数，n-1为次数（基函数的个数永远为次数+1。对应的点可以改变。注意，一直以来我说的基函数对应点，只是说的加权和时基函数与应与那个点组合相乘，实际上时每个点都有基函数的取值，因为t的值才是对应每个点）。算的时候下标变了代入原公式算就行。

基函数没有意义如下标为n,n-1时，默认为0。

参数矢量方程的求导，除非矢量未知，否则实际上就是对参数t求导。