0简介

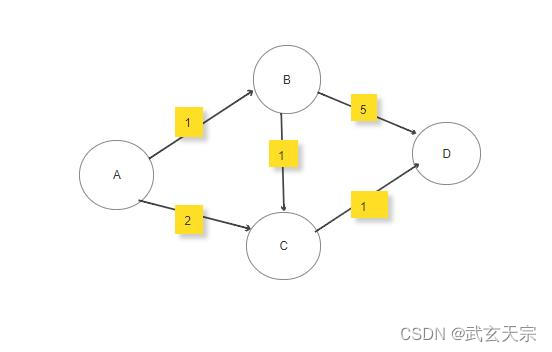
Dijkstra算法是一种计算某一顶点到其余顶点最短路径的算法。它采用了贪心的策略，实现时使用了广度优先。这个算法常学常忘，因此写篇博客彻底解决它。

1计算步骤介绍

Dijkstra的计算步骤不难，如下

(1)设置一个集合表示已经标记过的节点，初始化为空
(2)使用一个数组d记录所有节点与源节点s的距离，初始化d[s] = 0,其余设置为INF
(3)循环n次
{在未标记的节点中，选出d值最小的节点x；将x加入标记过节点的集合；对于从x出发的所有边(x,y)，更新d[y] = min(d[y],d[x]+w(x,y))
}

这个原理并不难，相信读者对照图论教科书多练习几遍即可手算，下面我们结合Leetcode上一道具体的题目来实现一下。

2 代码实战

下面是Leetcode743题的题干。这道题是Dijkstra算法一个典型应用，题目不难，使用Dijkstra算法计算出源节点到剩余节点的最小距离即可。最后返回到节点的最大值，如果这个图不是一个联通图，返回-1。

有 N 个网络节点，标记为 1 到 N。
给定一个列表 times，表示信号经过有向边的传递时间。 times[i] = (u, v, w)，其中 u 是源节点，v 是目标节点， w 是一个信号从源节点传递到目标节点的时间。
现在，我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1。
输入：times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
输出：2

对于实现Dijkstra算法来说，解决问题的首要问题是建立图。建图我们采用邻接表的方式，对于每一个点，所连接的点与权值。而在实现的时候呢，我们将它抽象为一个边(edge)，使用一个结构体Edge，其中u、v、d依次是源节点、目的节点、权值。

    struct Edge{int u,v,d;Edge(int from,int to,int dis):      u(from),v(to),d(dis){}};

所以建图时，我们使用一个vector<Edge> edges记录边，使用邻接表建图时只需记录源节点所在边在edges的下标就足够了。
建图完毕之后使用BFS实现原理部分的计算步骤即可，有一点值得注意的是计算步骤有一个步骤是在未标记的节点中，选出d值最小的节点x；对于这个步骤，我们可以使用一个优先队列优化一下，u是待标记的节点，d是与源节点的距离。这里重载了<使它在优先队列中升序排列。

    struct heapNode{int u,d;bool operator < (const heapNode& rhs) const{return d > rhs.d;}};

下面来看一下全部代码

class Solution {
public:struct Edge{int u,v,d;Edge(int from,int to,int dis):      u(from),v(to),d(dis){}};struct heapNode{int u,d;bool operator < (const heapNode& rhs) const{return d > rhs.d;}};int networkDelayTime(vector<vector<int>>& times, int N, int K) {priority_queue<heapNode> que;vector<Edge> edges;vector<vector<int>> g(N,vector<int>());vector<int> d(N,INT_MAX);d[K-1] = 0;vector<int> visited(N,0);for(int i = 0; i < times.size();++i)//建图{edges.push_back(Edge{times[i][0]-1,times[i][1]-1,times[i][2]});g[times[i][0]-1].push_back(edges.size()-1);}que.push(heapNode{K-1,0});//先把源节点加进去while(!que.empty()){heapNode node = que.top();que.pop();if(visited[node.u])continue;visited[node.u] = 1;//标记for(int i = 0; i < g[node.u].size(); ++i){Edge &edge = edges[g[node.u][i]];if(d[edge.v] > d[edge.u] + edge.d)//更新权值{d[edge.v] = d[edge.u] + edge.d;que.push(heapNode{edge.v,d[edge.v]});}}}int result = -1;for(int i = 0; i < d.size(); ++i){if(d[i] > result)result = d[i];}return result == INT_MAX ? -1 : result;//判断是否是连通图}
};