dijkstra

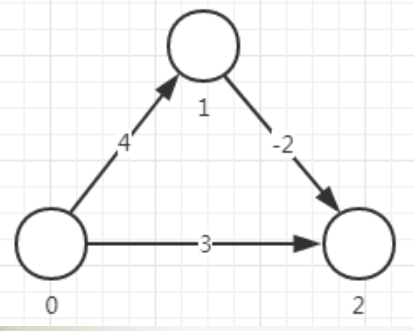
前提：在一张图里，不能有权值为负数的边。

给你一个出发点，求出发点到所有结点的最短距离是多少？如果无法到达某个点，则到这个点的距离是正无穷（一般出现在有向图里面）。

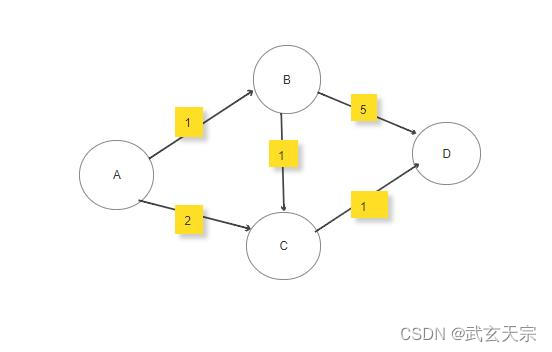
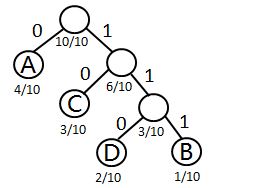
举个，例子，看如下图：右边集合表示的是A点到集合中各个点的最短距离。

一开始，假设A点到所有其它点的距离是正无穷，就是假设都不可到达：

A作为一个桥连点出现后，A到B点的距离就是原先A到A（0）的距离加上A到B的距离（1），后面的类似，所以得到如下图：

当A这个点的记录使用完了之后，就永远不去改动它，就是上图中圈起来的A点。然后在剩下的记录中选一个最小的记录；B点对应1，意思就是从原点出发到达B的距离是1，再以B作为桥连点往外找。发现B到C的距离为2，B到E的距离为170，所以可以更新表中C点的记录为3（AB+BC），E的记录更新为171（AB+BE）。之后B点这条记录也永远不去改动。在表中使用了哪条记录就将其锁住，再也不碰它。

接下来，就是C点。。。同样的逻辑玩下去。最终表里全部锁死的记录就是dijkstra要求的记录。

注意，中间如果碰到距离相同的可以不更新。这好像有点贪心思想啊。

但问题是如何在表里找最小的记录呢，可以每次遍历来找，但是有点麻烦。所以更好的方式是利用小根堆。

小根堆会自动组织好，每次把最小的值弹出来，但在这里我们还有一个要求，就是我们有可能要更改已经在堆里组织好的值，这样的话，系统提供的堆实现不了。我们需要手动改写堆！推荐看看这两篇文章——系统提供的堆 VS 手动改写堆 & 堆排序，，。可以更好理解dijkstra算法的改进。

然后我们依次来看自己手写的小根堆要实现的功能有哪些，

1）add()，添加一条记录的方法，就是从原点到某个点的距离是多少，并且按距离来组织

2）update()，更新的方法，需要更新某条记录的距离。比如原点到X点的距离是100，但是通过某个桥连点到X的距离是20了，所以这条记录的距离就要更新成20，并且这条记录要在小根堆里往上heapInsert()，自动组织好顺序

3）ignore()，忽略点某个已经使用过的结点的方法。

小根堆里装的东西的结构就是：

public static class NodeRecord {public Node node;public int distance;public NodeRecord(Node node, int distance) {this.node = node;this.distance = distance;}}

以下代码分别实现了dijkstra算法的两种方法

package com.harrison.class11;import java.util.HashMap;
import java.util.HashSet;
import java.util.Map.Entry;import com.harrison.class11.Code01_NodeEdgeGraph.*;public class Code07_dijkstra {// 从from点到key的最短距离是valuepublic static HashMap<Node, Integer> dijkstra1(Node from) {HashMap<Node, Integer> distanceMap = new HashMap<>();distanceMap.put(from, 0);// 一开始，自己到自己的距离当然是0// 锁住已经使用过的记录HashSet<Node> selectedNodes = new HashSet<>();Node minNode=getMinDistanceNodeAndUnselectedNode(distanceMap, selectedNodes);while(minNode!=null) {int distance=distanceMap.get(minNode);for(Edge edge:minNode.edges) {Node toNode=edge.to;if(!distanceMap.containsKey(toNode)) {distanceMap.put(toNode, distance+edge.weight);}else {distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance+edge.weight));}}selectedNodes.add(minNode);minNode=getMinDistanceNodeAndUnselectedNode(distanceMap, selectedNodes);}return distanceMap;}// 在distanceMap表里面排除掉在selectedNodes集合的点，然后选则距离最小的点返回public static Node getMinDistanceNodeAndUnselectedNode(HashMap<Node, Integer> distanceMap,HashSet<Node> selectedNodes) {Node minNode = null;int minDistance = Integer.MAX_VALUE;// EntrySet可以遍历HashMap中的值for(Entry<Node, Integer> entry:distanceMap.entrySet()) {Node node=entry.getKey();int distance=entry.getValue();if(!selectedNodes.contains(node) && distance<minDistance) {minNode=node;minDistance=distance;}}return minNode;}public static class NodeRecord{public Node node;public int distance;public NodeRecord(Node n,int d) {node=n;distance=d;}}public static class NodeHeap{// 实际的堆结构private Node[] nodes;// key在堆中的位置就是value// 如果value是-1代表这个结点曾经进过堆（进来之后弹出了）private HashMap<Node, Integer> heapIndexMap;// 源结点到key的最小距离就是valueprivate HashMap<Node, Integer> distanceMap;private int size;// 堆上有多少个点public NodeHeap(int size) {nodes=new Node[size];heapIndexMap=new HashMap<>();distanceMap=new HashMap<>();this.size=0;}public boolean isEmpty() {return size==0;}// 如果某个结点在heapIndexMap表有记录，表示曾经进过堆public Boolean isEntered(Node node) {return heapIndexMap.containsKey(node);}public boolean inHeap(Node node) {return isEntered(node) && heapIndexMap.get(node)!=-1;}public void heapInsert(Node node,int index) {while(distanceMap.get(nodes[index])<distanceMap.get(nodes[(index-1)/2])) {swap(index, (index-1)/2);index=(index-1)/2;}}public void heapfiy(int index,int size) {int left=2*index+1;while(left<size) {int smallest=(left+1<size) &&(distanceMap.get(nodes[left+1])<distanceMap.get(nodes[left]))?left+1:left;smallest=distanceMap.get(nodes[smallest])<distanceMap.get(nodes[index])?smallest:index;if(smallest==index) {break;}swap(smallest, index);index=smallest;left=2*index+1;}}private void swap (int index1,int index2) {heapIndexMap.put(nodes[index1], index2);heapIndexMap.put(nodes[index2], index1);Node tmp=nodes[index1];nodes[index1]=nodes[index2];nodes[index2]=tmp;}// 有一个点node，如果发现了一个从源节点到node的距离为distance// 判断要不要更新，如果需要更新，就更新public void addOrUpdateOrIgnore(Node node,int distance) {if(inHeap(node)) {// 如果结点在堆上，有可能更新完记录后，距离变小，所以需要调整堆distanceMap.put(node, Math.min(distanceMap.get(node), distance));heapInsert(node, heapIndexMap.get(node));}if(!isEntered(node)){// 如果没有进过堆，那么将这个结点挂在堆的最后一个结点nodes[size]=node;// 这个结点的位置就在heapIndexMap表的size位置上heapIndexMap.put(node, size);distanceMap.put(node, distance);heapInsert(node, size++);}// 如果两个if都没中，说明这个结点既不在堆上，但是又进来过，// 相当于什么都没做就直接返回}public NodeRecord pop(){NodeRecord nodeRecord=new NodeRecord(nodes[0], distanceMap.get(nodes[0]));swap(0, size-1);// 堆顶弹出后，标记为-1，并移除相应的距离记录heapIndexMap.put(nodes[size-1], -1);distanceMap.remove(nodes[size-1]);// 释放size-1位置上的东西nodes[size-1]=null;heapfiy(0, --size);return nodeRecord;}}// 改进后的dijkstra算法// 从head出发，所有head能到达的结点// 生成到达每个结点的最小路径记录并返回public static HashMap<Node, Integer> dijkstra2(Node head,int size){NodeHeap nodeHeap=new NodeHeap(size);nodeHeap.addOrUpdateOrIgnore(head, 0);HashMap<Node, Integer> ans=new HashMap<>();while(!nodeHeap.isEmpty()) {NodeRecord recored=nodeHeap.pop();Node cur=recored.node;int distance=recored.distance;for(Edge edge:cur.edges) {nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight+distance);}ans.put(cur, distance);}return ans;}
}