最近巩固一下算法，提高自己内力，网上看到查看到这篇介绍很详细的《Dijkstra迪杰斯特拉算法》，在这里转载记录一下。

1 前言

本章介绍迪杰斯特拉算法。和以往一样，本文会先对迪杰斯特拉算法的理论论知识进行介绍，然后给出C语言的实现。后续再分别给出C++和Java版本的实现。

2 迪杰斯特拉算法介绍

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

2.1 基本思想

通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是"起点s到该顶点的路径"。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 ... 重复该操作，直到遍历完所有顶点。

2.2 操作步骤

(1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

(2) 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

(4) 重复步骤(2)和(3)，直到遍历完所有顶点。

单纯的看上面的理论可能比较难以理解，下面通过实例来对该算法进行说明。

2.3 迪杰斯特拉算法图解

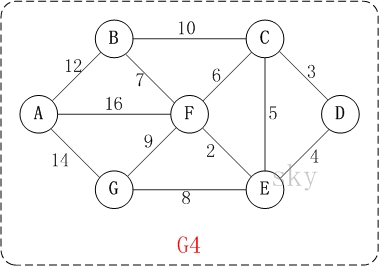
以上图G4为例，来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。

初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！

第1步：将顶点D加入到S中。
此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。
上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。
此时，S={D(0),C(3)}, U={A(∞),B(13),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。
上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。
此时，S={D(0),C(3),E(4)}, U={A(∞),B(13),F(6),G(12)}。

第4步：将顶点F加入到S中。
此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

3. 迪杰斯特拉算法实现

3.1 C实现

以"邻接矩阵"为例对迪杰斯特拉算法进行说明，对于"邻接表"实现的图在后面会给出相应的源码。

3.1.1. 基本定义

// 邻接矩阵
typedef struct _graph
{char vexs[MAX];       // 顶点集合int vexnum;           // 顶点数int edgnum;           // 边数int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;// 边的结构体
typedef struct _EdgeData
{char start; // 边的起点char end;   // 边的终点int weight; // 边的权重
}EData;

Graph是邻接矩阵对应的结构体。
vexs用于保存顶点，vexnum是顶点数，edgnum是边数；matrix则是用于保存矩阵信息的二维数组。例如，matrix[i][j]=1，则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点；matrix[i][j]=0，则表示它们不是邻接点。
EData是邻接矩阵边对应的结构体。

3.1.2. 迪杰斯特拉算法

/** Dijkstra最短路径。* 即，统计图(G)中"顶点vs"到其它各个顶点的最短路径。** 参数说明：*        G -- 图*       vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。*     prev -- 前驱顶点数组。即，prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。*     dist -- 长度数组。即，dist[i]是"顶点vs"到"顶点i"的最短路径的长度。*/
void dijkstra(Graph G, int vs, int prev[], int dist[])
{int i,j,k;int min;int tmp;int flag[MAX];      // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。// 初始化for (i = 0; i < G.vexnum; i++){flag[i] = 0;              // 顶点i的最短路径还没获取到。prev[i] = 0;              // 顶点i的前驱顶点为0。dist[i] = G.matrix[vs][i];// 顶点i的最短路径为"顶点vs"到"顶点i"的权。}// 对"顶点vs"自身进行初始化flag[vs] = 1;dist[vs] = 0;// 遍历G.vexnum-1次；每次找出一个顶点的最短路径。for (i = 1; i < G.vexnum; i++){// 寻找当前最小的路径；// 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。min = INF;for (j = 0; j < G.vexnum; j++){if (flag[j]==0 && dist[j]<min){min = dist[j];k = j;}}// 标记"顶点k"为已经获取到最短路径flag[k] = 1;// 修正当前最短路径和前驱顶点// 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。for (j = 0; j < G.vexnum; j++){tmp = (G.matrix[k][j]==INF ? INF : (min + G.matrix[k][j])); // 防止溢出if (flag[j] == 0 && (tmp  < dist[j]) ){dist[j] = tmp;prev[j] = k;}}}// 打印dijkstra最短路径的结果printf("dijkstra(%c): \n", G.vexs[vs]);for (i = 0; i < G.vexnum; i++)printf("  shortest(%c, %c)=%d\n", G.vexs[vs], G.vexs[i], dist[i]);
}

3.2 C++实现

3.2.1. 基本定义

class MatrixUDG {#define MAX    100#define INF    (~(0x1<<31))        // 无穷大(即0X7FFFFFFF)private:char mVexs[MAX];    // 顶点集合int mVexNum;             // 顶点数int mEdgNum;             // 边数int mMatrix[MAX][MAX];   // 邻接矩阵public:// 创建图(自己输入数据)MatrixUDG();// 创建图(用已提供的矩阵)//MatrixUDG(char vexs[], int vlen, char edges[][2], int elen);MatrixUDG(char vexs[], int vlen, int matrix[][9]);~MatrixUDG();// 深度优先搜索遍历图void DFS();// 广度优先搜索（类似于树的层次遍历）void BFS();// prim最小生成树(从start开始生成最小生成树)void prim(int start);// 克鲁斯卡尔（Kruskal)最小生成树void kruskal();// Dijkstra最短路径void dijkstra(int vs, int vexs[], int dist[]);// 打印矩阵队列图void print();private:// 读取一个输入字符char readChar();// 返回ch在mMatrix矩阵中的位置int getPosition(char ch);// 返回顶点v的第一个邻接顶点的索引，失败则返回-1int firstVertex(int v);// 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1int nextVertex(int v, int w);// 深度优先搜索遍历图的递归实现void DFS(int i, int *visited);// 获取图中的边EData* getEdges();// 对边按照权值大小进行排序(由小到大)void sortEdges(EData* edges, int elen);// 获取i的终点int getEnd(int vends[], int i);
};

MatrixUDG是邻接矩阵对应的结构体。
mVexs用于保存顶点，mVexNum是顶点数，mEdgNum是边数；mMatrix则是用于保存矩阵信息的二维数组。例如，mMatrix[i][j]=1，则表示"顶点i(即mVexs[i])"和"顶点j(即mVexs[j])"是邻接点；mMatrix[i][j]=0，则表示它们不是邻接点。

3.2.2. 迪杰斯特拉算法

/** Dijkstra最短路径。* 即，统计图中"顶点vs"到其它各个顶点的最短路径。** 参数说明：*       vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。*     prev -- 前驱顶点数组。即，prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。*     dist -- 长度数组。即，dist[i]是"顶点vs"到"顶点i"的最短路径的长度。*/
void MatrixUDG::dijkstra(int vs, int prev[], int dist[])
{int i,j,k;int min;int tmp;int flag[MAX];      // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。// 初始化for (i = 0; i < mVexNum; i++){flag[i] = 0;              // 顶点i的最短路径还没获取到。prev[i] = 0;              // 顶点i的前驱顶点为0。dist[i] = mMatrix[vs][i]; // 顶点i的最短路径为"顶点vs"到"顶点i"的权。}// 对"顶点vs"自身进行初始化flag[vs] = 1;dist[vs] = 0;// 遍历mVexNum-1次；每次找出一个顶点的最短路径。for (i = 1; i < mVexNum; i++){// 寻找当前最小的路径；// 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。min = INF;for (j = 0; j < mVexNum; j++){if (flag[j]==0 && dist[j]<min){min = dist[j];k = j;}}// 标记"顶点k"为已经获取到最短路径flag[k] = 1;// 修正当前最短路径和前驱顶点// 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。for (j = 0; j < mVexNum; j++){tmp = (mMatrix[k][j]==INF ? INF : (min + mMatrix[k][j]));if (flag[j] == 0 && (tmp  < dist[j]) ){dist[j] = tmp;prev[j] = k;}}}// 打印dijkstra最短路径的结果cout << "dijkstra(" << mVexs[vs] << "): " << endl;for (i = 0; i < mVexNum; i++)cout << "  shortest(" << mVexs[vs] << ", " << mVexs[i] << ")=" << dist[i] << endl;
}

3.3 迪杰斯特拉算法---Java实现

java的实现和C++实现基本上一样的了

4. 迪杰斯特拉算法的源码

这里分别给出"邻接矩阵图"和"邻接表图"的迪杰斯特拉算法源码。

1. 邻接矩阵源码(matrix_udg.c)

2. 邻接表源码(list_udg.c)

############################################################

参考2

Dijkstra算法

1.定义概览

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

2.算法描述

1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2)算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

执行动画过程如下图

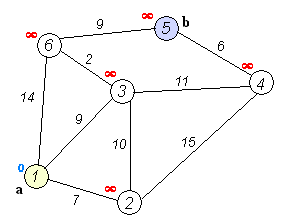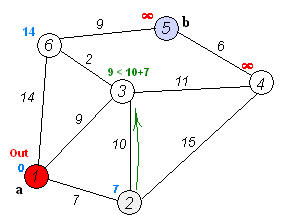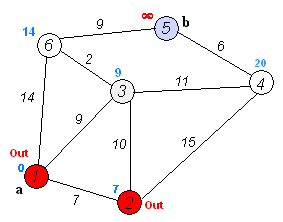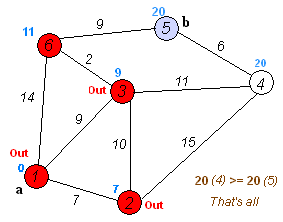
3.算法代码实现：

const int  MAXINT = 32767;
const int MAXNUM = 10;
int dist[MAXNUM];
int prev[MAXNUM];int A[MAXUNM][MAXNUM];void Dijkstra(int v0)
{bool S[MAXNUM];                                  // 判断是否已存入该点到S集合中int n=MAXNUM;for(int i=1; i<=n; ++i){dist[i] = A[v0][i];S[i] = false;                                // 初始都未用过该点if(dist[i] == MAXINT)    prev[i] = -1;else prev[i] = v0;}dist[v0] = 0;S[v0] = true; 　　for(int i=2; i<=n; i++){int mindist = MAXINT;int u = v0; 　　                            // 找出当前未使用的点j的dist[j]最小值for(int j=1; j<=n; ++j)if((!S[j]) && dist[j]<mindist){u = j;                             // u保存当前邻接点中距离最小的点的号码 mindist = dist[j];}S[u] = true; for(int j=1; j<=n; j++)if((!S[j]) && A[u][j]<MAXINT){if(dist[u] + A[u][j] < dist[j])     //在通过新加入的u点路径找到离v0点更短的路径  {dist[j] = dist[u] + A[u][j];    //更新dist prev[j] = u;                    //记录前驱顶点 }}}
}

4.算法实例

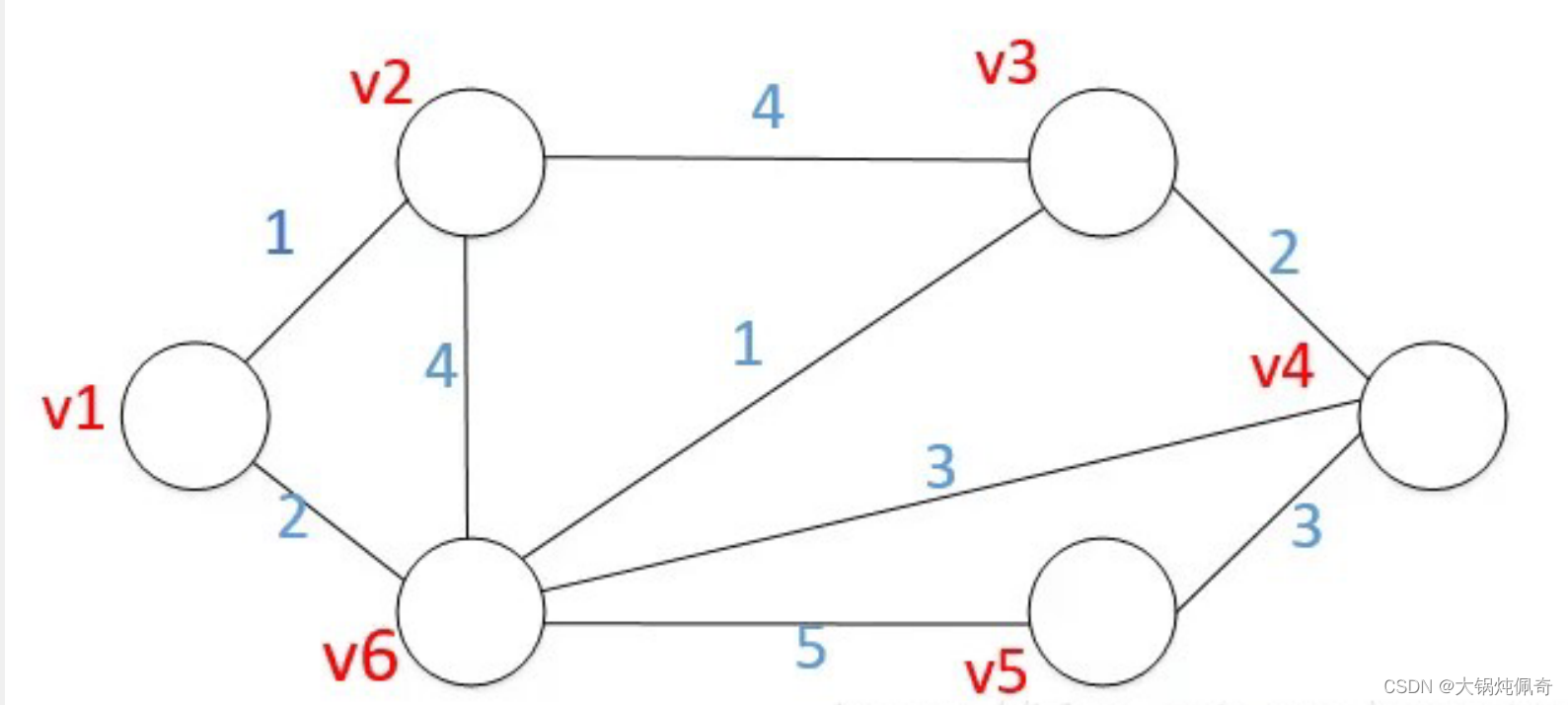
先给出一个无向图

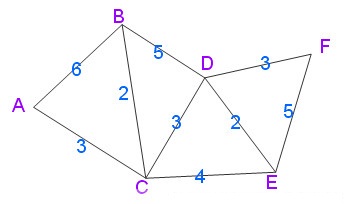
用Dijkstra算法找出以A为起点的单源最短路径步骤如下

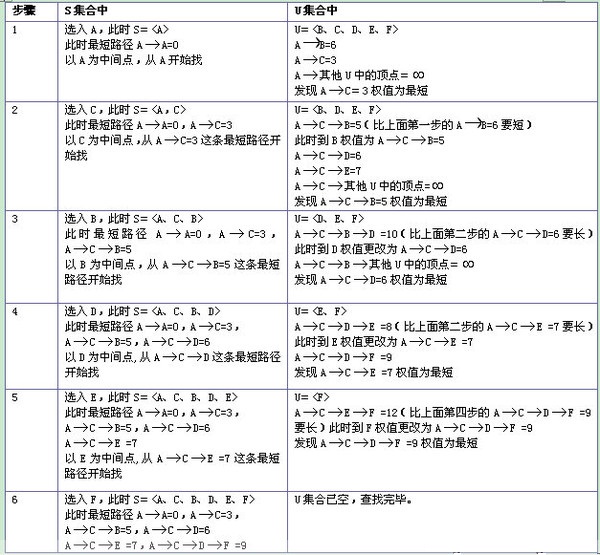
Floyd算法

1.定义概览

Floyd-Warshall算法（Floyd-Warshall algorithm）是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3)，空间复杂度为O(N2)。

2.算法描述

1)算法思想原理：

Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）

从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

2).算法描述：

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。　　

b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

3).Floyd算法过程矩阵的计算----十字交叉法

方法：两条线，从左上角开始计算一直到右下角如下所示

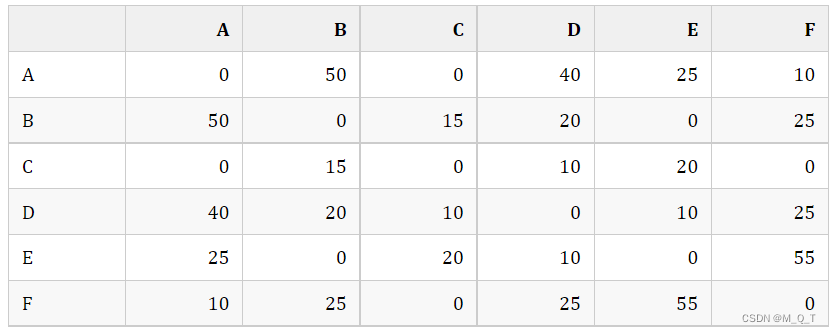
给出矩阵，其中矩阵A是邻接矩阵，而矩阵Path记录u,v两点之间最短路径所必须经过的点

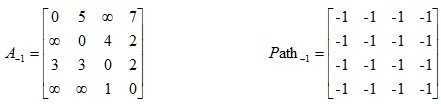
相应计算方法如下：

最后A3即为所求结果

3.算法代码实现

typedef struct          
{        char vertex[VertexNum];                                //顶点表         int edges[VertexNum][VertexNum];                       //邻接矩阵,可看做边表         int n,e;                                               //图中当前的顶点数和边数         
}MGraph; void Floyd(MGraph g)
{int A[MAXV][MAXV];int path[MAXV][MAXV];int i,j,k,n=g.n;for(i=0;i<n;i++)for(j=0;j<n;j++){ 　　A[i][j]=g.edges[i][j];path[i][j]=-1;}for(k=0;k<n;k++){ for(i=0;i<n;i++)for(j=0;j<n;j++)if(A[i][j]>(A[i][k]+A[k][j])){A[i][j]=A[i][k]+A[k][j];path[i][j]=k;} } 
}

算法时间复杂度:O(n3)