问题描述

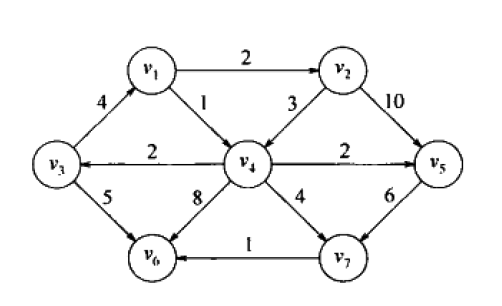
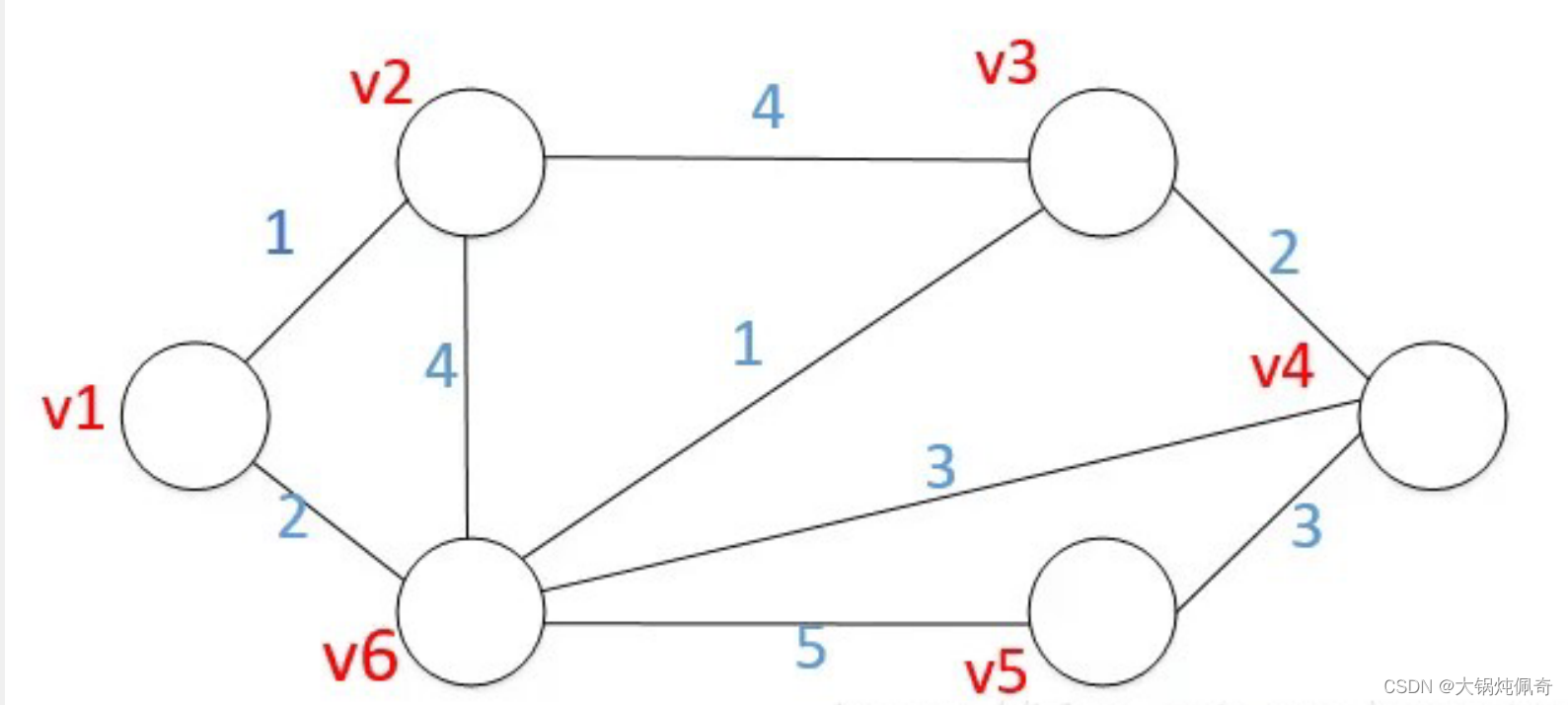
现有一个有向赋权图。如下图所示：
这里写图片描述
问题：根据每条边的权值，求出从起点s到其他每个顶点的最短路径和最短路径的长度。
说明：不考虑权值为负的情况，否则会出现负值圈问题。
s：起点
v：算法当前分析处理的顶点
w：与v邻接的顶点
$d_v$ ：从s到v的距离
$d_w$ ：从s到w的距离
$c_{v,w}$ ：顶点v到顶点w的边的权值

问题分析

Dijkstra算法按阶段进行，同无权最短路径算法（先对距离为0的顶点处理，再对距离为1的顶点处理，以此类推）一样，都是先找距离最小的。
在每个阶段，Dijkstra算法选择一个顶点v，它在所有unknown顶点中具有最小的 $d_v$ ，同时算法声明从s到v的最短路径是known的。阶段的其余部分为，对w的 $d_v$ （距离）和 $p_v$ （上一个顶点）更新工作（当然也可能不更新）。
在算法的每个阶段，都是这样处理的：
【0.5】在无权的情况下，若 $d_w$ = $\infty$ 则置 $d_w=d_v+1$ （无权最短路径）
【1】在有权的情况下，若 $d_w$ = $\infty$ 则置 $d_w=d_v+c_{v,w}$
【2】若 $d_w$ ！= $\infty$ ，开始分析：从顶点v到顶点w的路径，若能使得w的路径长比w原来的路径长短一点，那么就需要对w进行更新，否则不对w更新。即满足 $d_v+c_{v,w}<d_w$ 时，就需要把 $d_w$ 的值更新为 $d_v+c_{v,w}$ ，同时顶点w的 $p_v$ 值得改成顶点v

实现过程

考虑Dijkstra算法过程中，有一个数据变化表。
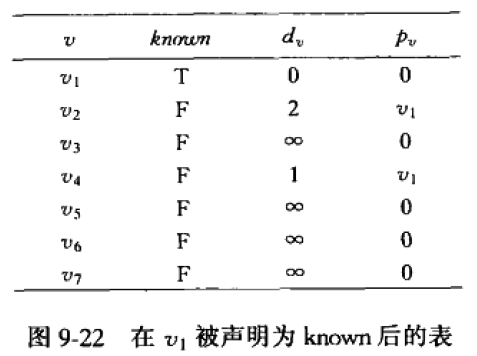
这里写图片描述

初始状态如上。开始顶点s是 $v_1$ ，所有顶点都是unknown的。 $v_1$ 的 $d_v$ 的值为0，因为它是起点。

【1】选择unknown顶点中， $d_v$ 值最小的顶点，即顶点 $v_1$ 。首先将 $v_1$ 标记为known。对与 $v_1$ 邻接的顶点 $v_2 v_4$ 进行调整： $v_2$ 的距离变为 $d_v+c_{v,w}$ 即 $v_1$ 的 $d_v$ 值+ $c_{1,2}$ 即0+2=2， $v_2$ 的 $p_v$ 值变为 $v_1$ ；同理，对 $v_4$ 作相应的处理。
这里写图片描述
【2】选择unknown顶点中， $d_v$ 值最小的顶点，即顶点 $v_4$ （其距离为1，最小）。将 $v_4$ 标记为known。对其邻接的顶点 $v_3 v_5 v_6 v_7$ 作相应的处理。

【3】选择unknown顶点中， $d_v$ 值最小的顶点，即顶点 $v_2$ （其距离为2，最小）。将 $v_2$ 标记为known。对其邻接的顶点 $v_4v_5$ 作相应的处理。但 $v_4$ 是已知的，所以不需要调整；因为经过 $v_2$ 到 $v_5$ 的距离为2+10=12，而s到 $v_5$ 路径为3是已知的（上表中， $v_5$ 的 $d_v$ 为3），12>3，所以也不需要也没有必要调整。
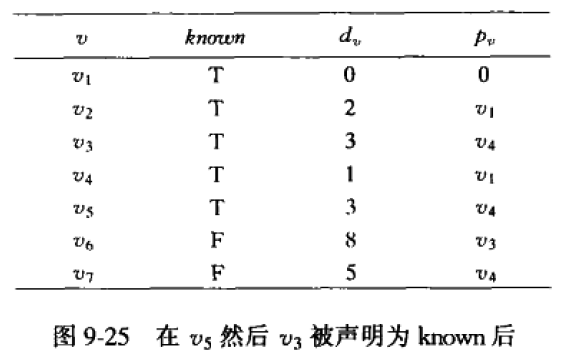
这里写图片描述
【4】选择unknown顶点中， $d_v$ 值最小的顶点，即顶点 $v_5$ （距离为3，最小，其实还有 $v_3$ 也是距离为3，但博主发现这里，先 $v_5$ 再 $v_3$ 和先 $v_3$ 再 $v_5$ 的运行结果都是一样的）。将 $v_5$ 标记为known。对其邻接的顶点 $v_7$ 作相应的处理。但原路径长更小，所以不用调整。
【5】再对 $v_3$ 处理。对 $v_6$ 的距离下调到3+5=8
这里写图片描述
【6】再对 $v_7$ 处理。对 $v_6$ 的距离下调到5+1=6

【7】最后，再对 $v_6$ 处理。不需调整。

上述实现过程对应的算法，可能需要用到优先队列，每次出队 $d_v$ 值最小的顶点，因为如果只是遍历来找到 $d_v$ 值最小的顶点，可能会花费很多时间。

如何使用数据变化表

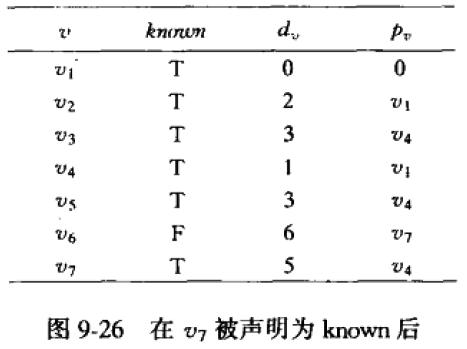
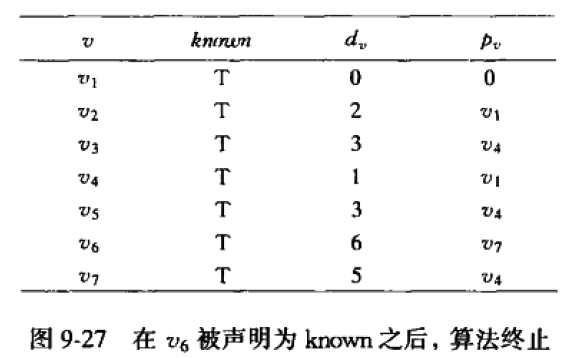
数据变化表的最终情况如下：
这里写图片描述
现在我们能找到起点 $v_1$ 到任意的 $v_i$ （除了起点）的最短路径，及其最短路径长。
比如，找到 $v_1$ 到 $v_3$ 的最短路径。
【1】 $v_3$ 的 $d_v$ 值为3，所以最短路径长为3
【2】 $v_3$ 的 $p_v$ 值为 $v_4$ ，所以 $v_3$ 的上一个顶点为 $v_4$
【3】到代表 $v_4$ 的第四行，发现 $v_4$ 的 $p_v$ 值为 $v_1$ ，所以 $v_4$ 的上一个顶点为 $v_1$
【4】 $v_1$ 是起点，结束。 $v_3$ 上一个是 $v_4$ ， $v_4$ 上一个是 $v_1$ ，反过来就得到了最短路径 $v_1=>v_4=>v_3$
上述分析，其实就是求最短路径的算法的思想：在对每个顶点对象进行处理后变成数据变化表的最终情况后，可以通过对任意顶点 $v_i$ 的 $p_v$ 值，回溯得到反转的最短路径。

代码实现

纸上得来终觉浅，绝知此事要躬行！使用python3来实现功能。
本文提到，将使用优先队列来实现寻找未知顶点中，具有最小dist的顶点。使用python已有实现好的优先队列。但实验中报错如下：
这里写图片描述
意思，Vertex实例并不支持小于比较运算符。所以需要实现Vertex类的__lt__方法。下面科普一下：

方法名	比较运算符	含义
`__eq__`	==	equal
`__lt__`	<	less than
`__le__`	<=	less and equal
`__gt__`	>	greater than
`__ge__`	>=	greater and equal

但很遗憾，python库自带的优先队列from queue import PriorityQueue，并不满足本文的需求。当PriorityQueue的元素为对象时，需要该对象的class实现__lt__函数，在往优先队列里添加元素时，内部是用的堆排序，堆排序的特点为每个堆（以及每个子堆）的第一个元素总是那个最小的元素。关键在于，在建立了这个堆后，堆就已经记录下来了创建堆时各个元素的大小关系了，在创建优先队列后，再改变某个对象的值，这个堆的结构是肯定不会变的，所以这种堆排序造成了排序是一次性的，如果之后某个对象的属性发生变化，堆的结构也不会随之而改变。
或者说，我们想要的优先队列肯定不是系统提供的优先队列，因为我们要支持可变对象的成员修改导致堆的改变，解决方案有三种，1.内部使用的堆排序的堆，最起码要支持，删除任意节点和增加节点操作（因为这两步就可以达到修改的效果了）2.这个内部堆，在执行出队操作时，考察哪个节点有修改操作，再把堆改变到正确的形态，再出队3.维护一个list，进行排降序，然后每改变一个可变对象的值，就对这个对象进行冒泡或者二分查找找到位置（因为别的都是已经排好序的了，只有它不在正确的位置），最后再list.pop()，但第三个方案是我后来想到的，所以下面代码并不是这样实现的，读者可以进行尝试，肯定比每次遍历全部快。
应该说，可能用不上队列了。我们可能只需要一个list或者set来存储v，在出队前随便vi改变其dist，在出队时再遍历找到最小的dist的vi，再删除掉这个vi即可。因为vi的dist一直在变，需求特殊，但是没必要专门造个轮子（感觉这个轮子也不好造），虽然时间复杂度可能高了点，但代码简单了啊。

优先队列中的堆排序

失效代码如下：三个节点对象的dist都是无穷大，在三个对象都进入队列，再把v3的dist改成0，想要的效果是出队出v3，但出队出的是v1。原因如上：

from queue import PriorityQueue
class Vertex:#顶点类def __init__(self,vid,dist):self.vid = vidself.dist = distdef __lt__(self,other):return self.dist < other.dist   
v1=Vertex(1,float('inf'))
v2=Vertex(2,float('inf'))
v3=Vertex(3,float('inf'))vlist = [v1,v2,v3]
q = PriorityQueue()for i in range(0,len(vlist)):q.put(vlist[i])
v3.dist = 0print('vid:',q.get().vid)#结果为vid: 1

而如果将在入队前，就把dist改变了，就能正确的出队。

v3.dist = 0
for i in range(0,len(vlist)):q.put(vlist[i])
#结果为vid: 3

使用set代替优先队列

class Vertex:#顶点类def __init__(self,vid,outList):self.vid = vid#当前顶点idself.outList = outList#当前顶点的出边（有向边）指向的顶点的id的列表，也可以理解为邻接表self.know = False#默认为假self.dist = float('inf')#s到该点的距离,默认为无穷大self.prev = 0#上一个顶点的id，默认为0def __eq__(self, other):if isinstance(other, self.__class__):return self.vid == other.videlse:return Falsedef __hash__(self):return hash(self.vid)#创建顶点对象
v1=Vertex(1,[2,4])
v2=Vertex(2,[4,5])
v3=Vertex(3,[1,6])
v4=Vertex(4,[3,5,6,7])
v5=Vertex(5,[7])
v6=Vertex(6,[])
v7=Vertex(7,[6])
#存储边的权值
edges = dict()
def add_edge(front,back,value):edges[(front,back)]=value
add_edge(1,2,2)
add_edge(1,4,1)
add_edge(3,1,4)
add_edge(4,3,2)
add_edge(2,4,3)
add_edge(2,5,10)
add_edge(4,5,2)
add_edge(3,6,5)
add_edge(4,6,8)
add_edge(4,7,4)
add_edge(7,6,1)
add_edge(5,7,6)
#创建一个长度为8的数组，来存储顶点，0索引元素不存
vlist = [False,v1,v2,v3,v4,v5,v6,v7]
#使用set代替优先队列，选择set主要是因为set有方便的remove方法
vset = set([v1,v2,v3,v4,v5,v6,v7])def get_unknown_min():#此函数则代替优先队列的出队操作the_min = 0the_index = 0j = 0for i in range(1,len(vlist)):if(vlist[i].know is True):continueelse:if(j==0):the_min = vlist[i].distthe_index = ielse:if(vlist[i].dist < the_min):the_min = vlist[i].distthe_index = i                    j += 1#此时已经找到了未知的最小的元素是谁vset.remove(vlist[the_index])#相当于执行出队操作return vlist[the_index]def main():#将v1设为顶点v1.dist = 0while(len(vset)!=0):v = get_unknown_min()print(v.vid,v.dist,v.outList)v.know = Truefor w in v.outList:#w为索引if(vlist[w].know is True):continueif(vlist[w].dist == float('inf')):vlist[w].dist = v.dist + edges[(v.vid,w)]vlist[w].prev = v.videlse:if((v.dist + edges[(v.vid,w)])<vlist[w].dist):vlist[w].dist = v.dist + edges[(v.vid,w)]vlist[w].prev = v.videlse:#原路径长更小，没有必要更新pass
main()
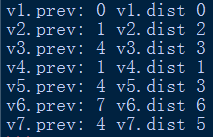
print('v1.prev:',v1.prev,'v1.dist',v1.dist)
print('v2.prev:',v2.prev,'v2.dist',v2.dist)
print('v3.prev:',v3.prev,'v3.dist',v3.dist)
print('v4.prev:',v4.prev,'v4.dist',v4.dist)
print('v5.prev:',v5.prev,'v5.dist',v5.dist)
print('v6.prev:',v6.prev,'v6.dist',v6.dist)
print('v7.prev:',v7.prev,'v7.dist',v7.dist)

这里写图片描述
运行结果与数据变化表的最终情况一致。

得到最短路径

把以下代码和以上代码合起来就可以运行成功，使用递归的思想来做：

def real_get_traj(start,index):traj_list = []def get_traj(index):#参数是顶点在vlist中的索引if(index == start):#终点traj_list.append(index)print(traj_list[::-1])#反转listreturnif(vlist[index].dist == float('inf')):print('从起点到该顶点根本没有路径')returntraj_list.append(index)get_traj(vlist[index].prev)get_traj(index)print('该最短路径的长度为',vlist[index].dist)real_get_traj(1,3)
real_get_traj(1,6)

这里写图片描述
如图所示，从v1到v3的最短路径为：[1, 4, 3]
从v1到v6的最短路径为：[1, 4, 7, 6]

负权边

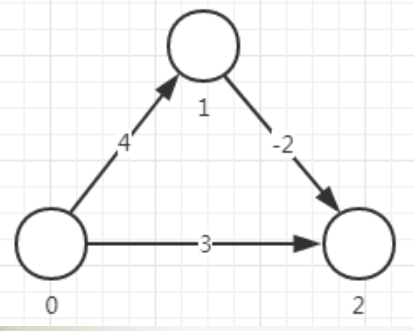
这里写图片描述
Dijkstra算法要求边上的权值不能为负数，不然就会出错。如上，本来最短路径是012，但由于算法是贪心的，所以只会直接选择到2

算法改进（若为无圈图）

注意，只有有向无圈图才有拓扑排序。

如果知道图是无圈图，那么我们可以通过改变声明顶点为known的顺序（原本这个顺序是，每次从unknown里面找出个最小dist的顶点），或者叫做顶点选取法则，来改进Dijkstra算法。新法则以拓扑排序选择顶点。由于选择和更新（每次选择和更新完成后，就会变成数据变化表中的某一种情况）可以在拓扑排序执行的时候进行，因此算法能一趟完成。

因为当一个顶点v被选取以后，按照拓扑排序的法则它肯定没有任何unknown顶点到v（指明方向）的入边，因为v的距离 $d_v$ 不可能再下降了（因为根本没有别的路到v了），所以这种选择方法是可行的。

使用这种方法不需要优先队列。