本文总结了图的几种最短路径算法的实现：深度或广度优先搜索算法，弗洛伊德算法，迪杰斯特拉算法，Bellman-Ford算法

1），深度或广度优先搜索算法（解决单源最短路径）
从起始结点开始访问所有的深度遍历路径或广度优先路径，则到达终点结点的路径有多条，取其中路径权值最短的一条则为最短路径。

下面是核心代码：

例1：下面是城市的地图，注意是单向图，求城市1到城市5的最短距离。(引用的是上次总结的图论（一）中1）的例2)

程序运行结果如下：

2），弗洛伊德算法（解决多源最短路径）：时间复杂度O(n^3),空间复杂度O(n^2)
基本思想：最开始只允许经过1号顶点进行中转，接下来只允许经过1号和2号顶点进行中转......允许经过1~n号所有顶点进行中转，来不断动态更新任意两点之间的最短路程。即求从i号顶点到j号顶点只经过前k号点的最短路程。

分析如下：1，首先构建邻接矩阵Floyd[n+1][n+1]，假如现在只允许经过1号结点，求任意两点间的最短路程，很显然Floyd[i][j] = min{Floyd[i][j], Floyd[i][1]+Floyd[1][j]}，代码如下：

2，接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短距离，在已经实现了从i号顶点到j号顶点只经过前1号点的最短路程的前提下，现在再插入第2号结点，来看看能不能更新更短路径，故只需在步骤1求得的Floyd[n+1][n+1]基础上，进行Floyd[i][j] = min{Floyd[i][j], Floyd[i][2]+Floyd[2][j]}；......
3，很显然，需要n次这样的更新，表示依次插入了1号，2号......n号结点，最后求得的Floyd[n+1][n+1]是从i号顶点到j号顶点只经过前n号点的最短路程。故核心代码如下：

例1：寻找最短的从商店到赛场的路线。其中商店在1号结点处，赛场在n号结点处，1~n结点中有m条线路双向连接。

程序运行结果如下：

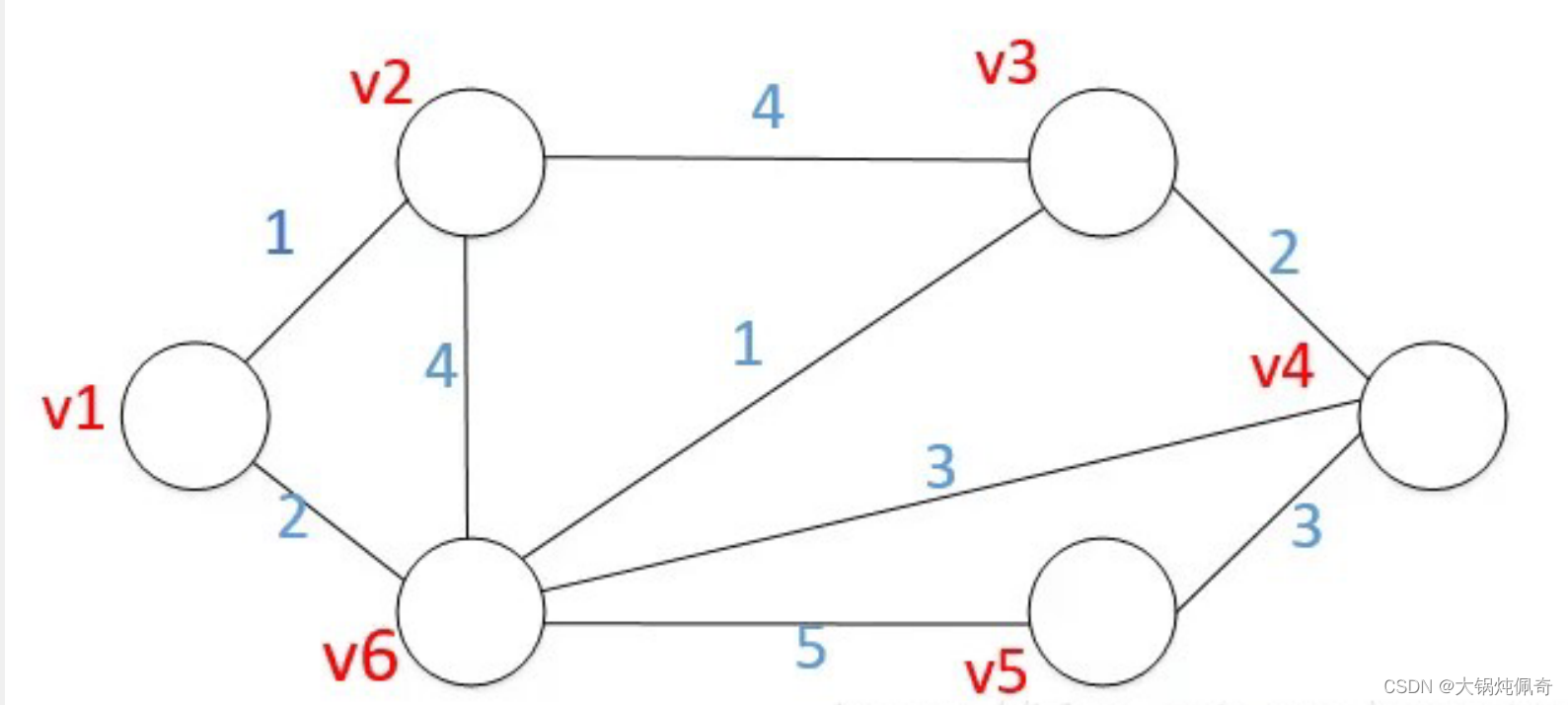
3），迪杰斯特拉算法（解决单源最短路径）
基本思想：每次找到离源点（如1号结点）最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。
基本步骤：1，设置标记数组book[]：将所有的顶点分为两部分,已知最短路径的顶点集合P和未知最短路径的顶点集合Q，很显然最开始集合P只有源点一个顶点。book[i]为1表示在集合P中；
2，设置最短路径数组dst[]并不断更新：初始状态下，令dst[i] = edge[s][i](s为源点，edge为邻接矩阵)，很显然此时dst[s]=0，book[s]=1。此时，在集合Q中可选择一个离源点s最近的顶点u加入到P中。并依据以u为新的中心点，对每一条边进行松弛操作(松弛是指由结点s-->j的途中可以经过点u，并令dst[j]=min{dst[j], dst[u]+edge[u][j]})，并令book[u]=1;
3，在集合Q中再次选择一个离源点s最近的顶点v加入到P中。并依据v为新的中心点，对每一条边进行松弛操作(即dst[j]=min{dst[j], dst[v]+edge[v][j]}),并令book[v]=1;
4，重复3，直至集合Q为空。
以下是图示：

核心代码如下所示：

例1：给你n个点，m条无向边，每条边都有长度d和花费p，给你起点s，终点t，要求输出起点到终点的最短距离及其花费，如果最短距离有多条路线，则输出花费最少的。
输入：输入n,m，点的编号是1~n,然后是m行，每行4个数 a,b,d,p，表示a和b之间有一条边，且其长度为d，花费为p。最后一行是两个数s,t;起点s，终点 t。n和m为 0 时输入结束。(1<n<=1000, 0<m<100000, s != t)
输出：输出一行，有两个数， 最短距离及其花费。
分析：由于每条边有长度d和花费p，最好构建边结构体存放，此外可以使用邻接链表，使用邻接链表时需要将上面的核心代码修改几个地方：

1，初始化dst[]时使用结点1的邻接链表；
2，更新最短路径数组时，k的范围由1~n变为1~edge[u].size()。先采用邻接矩阵解决此题，再使用邻接表解决此题，两种方法的思路都一样：初始化邻接矩阵或邻接链表，并
初始化最短路径数组dst ----> n-1轮边的松弛中，先找到离新源点最近的中心点u，之后根据中心点u为转折点来更新路径数组。

使用邻接矩阵求解：

程序运行结果如下：

使用邻接链表求解：

程序运行结果如下：

使用邻接表时，注意更新dst[]，book[]时要使用邻接表元素对应下标中的next成员，而涉及到权值加减时时需要使用邻接表中的对应下标来取得权值；而使用邻接矩阵就没这么多顾虑了，因为这时候邻接矩阵对应下标和dst[]要更新元素的下标正好一致，都是从1开始编号。

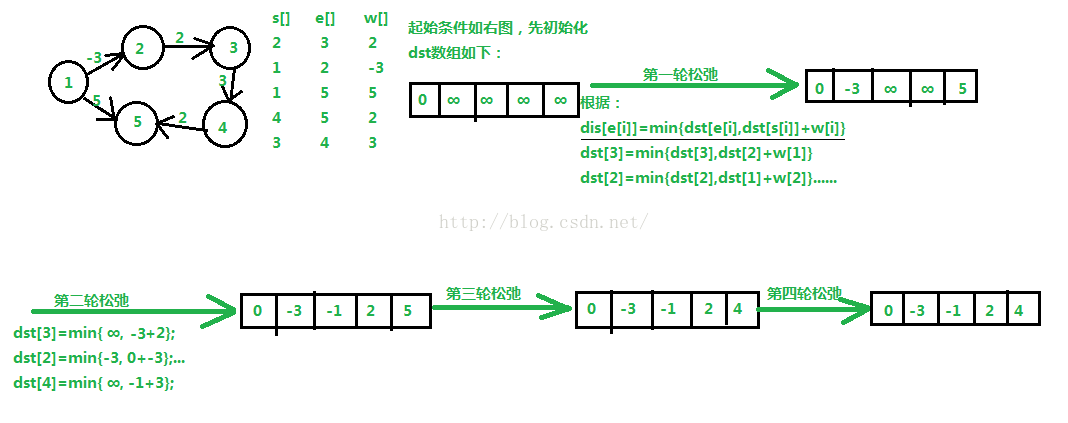
4），Bellman-Ford算法(解决负权边，解决单源最短路径，前几种方法不能求含负权边的图)：：时间复杂度O(nm),空间复杂度O(m)
主要思想：对所有的边进行n-1轮松弛操作，因为在一个含有n个顶点的图中，任意两点之间的最短路径最多包含n-1边。换句话说，第1轮在对所有的边进行松弛后，得到的是从1号顶点只能经过一条边到达其余各定点的最短路径长度。第2轮在对所有的边进行松弛后，得到的是从1号顶点只能经过两条边到达其余各定点的最短路径长度，......
以下是图示：

此外，Bellman_Ford还可以检测一个图是否含有负权回路：如果在进行n-1轮松弛后仍然存在dst[e[i]] > dst[s[i]]+w[i]。算法核心代码如下：

例1：对图示中含负权的有向图，输出从结点1到各结点的最短路径，并判断有无负权回路。

程序运行结果如下：

原文：http://blog.csdn.net/qibofang/article/details/51594673#