前言：

最短路径算法：用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

例子：

暑期，你想要出门去旅游，但是在你出发之前，你想知道任意两个城市之间的最短距离。

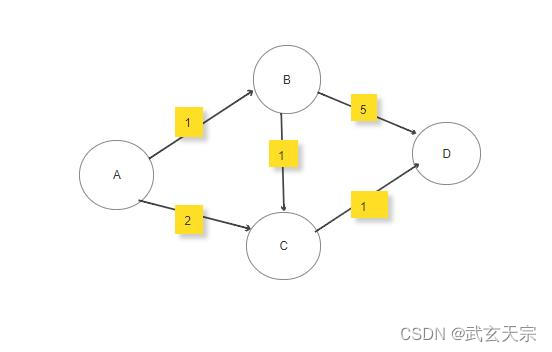
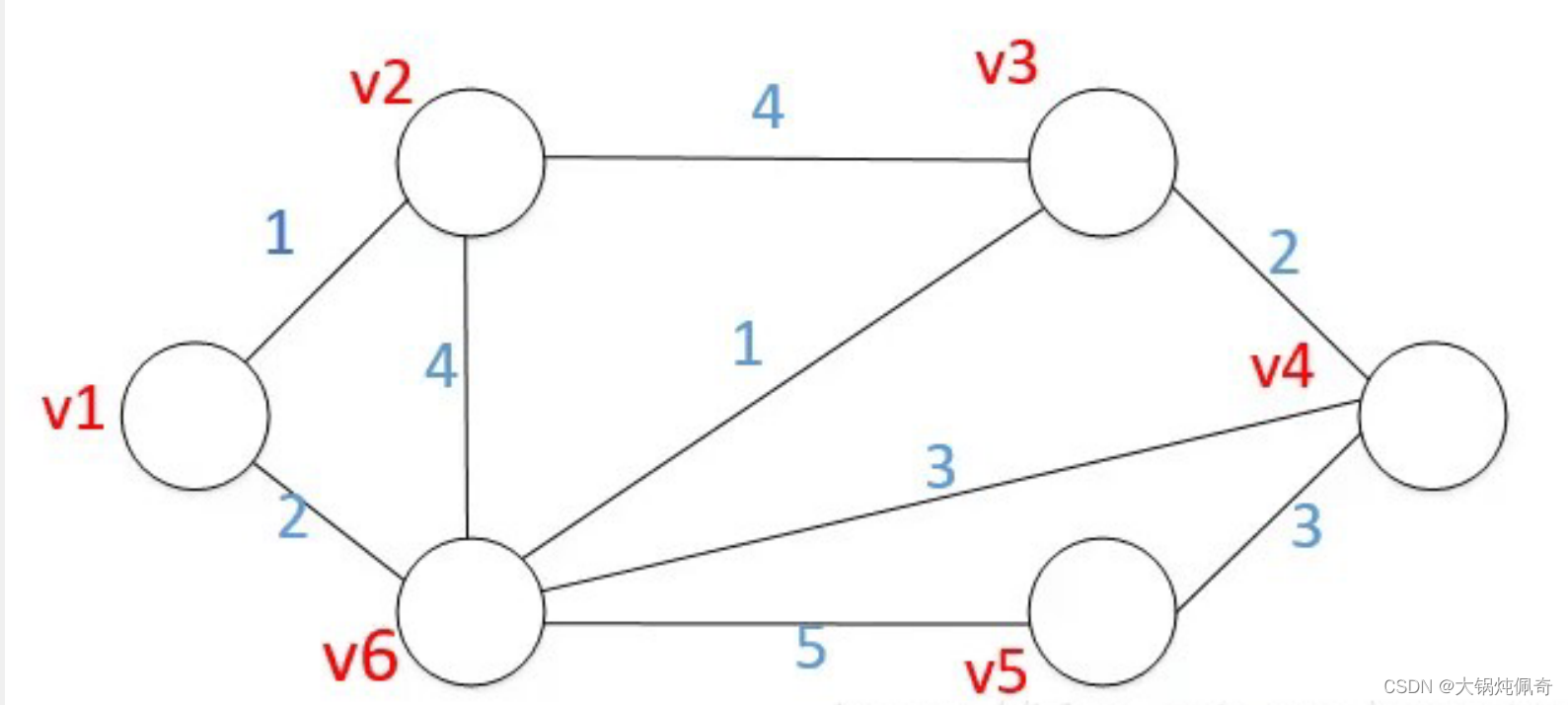
给出地图：

                                

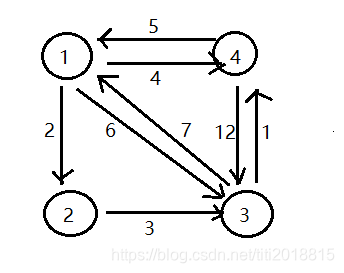
给出数据：

4 8

1 2 2

1 3 6

1 4 4

2 3 3

3 1 7

3 4 1

4 1 5

4 3 12

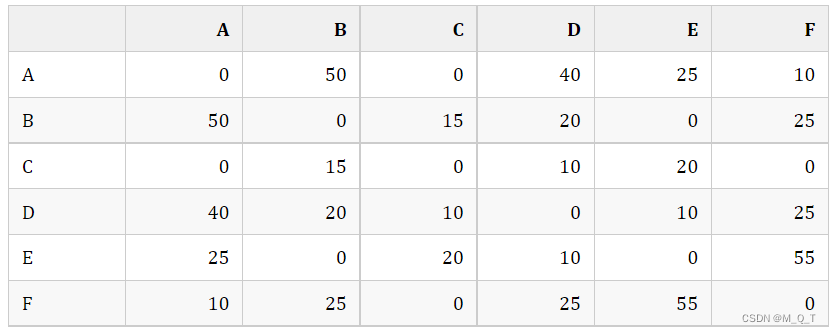
把数据转换成邻接矩阵：

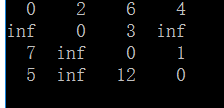
1.Floyd-Warshall算法

思路：

在邻接矩阵中，依次把每一个点作为中间点，进行中转；

代码如下：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;const int inf=99999999;
const int N=101;int map[N][N];//存储城市之间的距离；
int n,m;
int aa,bb,cc;void init()//初始化；
{for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j)map[i][j]=0;elsemap[i][j]=inf;}}
}int main()
{while(~scanf("%d%d",&n,&m)){init();for(int i=0;i<m;i++){scanf("%d%d%d",&aa,&bb,&cc);map[aa][bb]=cc;}for(int k=1;k<=n;k++)//中转点；{for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(map[i][j]>map[i][k]+map[k][j])map[i][j]=map[i][k]+map[k][j];}}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){printf("%10d",map[i][j]);}printf("\n");}}return 0;
}

2.Dijkstra算法----单源最短路

思路：

1.将所有的顶点分成两个部分：已知最短路程的顶点集合P和未知的最短路径的顶点集合Q。最开始，已知最短路径的定点集合P中只有源点一个顶点。我们这里用一个book数组来记录哪些点在集合中。例如，如果book[i]为1，代表这个顶点在集合P中，否则不在集合P中，在集合Q中。

2.设置源点s到自己的最短路径为0，即dis[s]=0。若存在有源点能直接到达的顶点 i，则把dis[i]设置为map[s][i]。同时，把所有其他（源点不能直接到达的）顶点的最短路径设为无穷大；

3.在集合Q的所有顶点中选择一个离源点s最近的顶点u（即dis[u]最小），加入到集合P中，并考察所有以u为起点的边，对每一条边进行松弛操作。例如，存在一条边从u到v的边，那么可以通过将边（u,v），添加到尾部来拓展一条从s到v的路径，这条路径的长度是dis[u]+map[u][v]。如果这个值比以前已知的dis[v]的值要小，那么我们就可以用新值来替代当前的dis[v];

4.重复第3步，如果集合Q为空，算法结束。最终dis数组中存储的值就是源点到各个点的距离；

代码如下：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;const int inf=99999999;
const int N=101;int map[N][N];//存储城市之间的距离；
int book[N];//记录点是否已经最短路径中；
int dis[N];//记录到源点的距离；
int n,m;
int aa,bb,cc;
int minn,u;void init()//初始化；
{for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j)map[i][j]=0;elsemap[i][j]=inf;}}
}void Dijkstra()
{for(int i=1;i<n;i++){minn=inf;for(int j=1;j<=n;j++)//选取最小的顶点加入最短路径；{if(book[j]==0&&dis[j]<minn){minn=dis[j];u=j;}}book[u]=1;for(int v=1;v<=n;v++){if(map[u][v]<inf)//松弛；{if(dis[v]>dis[u]+map[u][v])dis[v]=dis[u]+map[u][v];}}}for(int i=1;i<=n;i++)printf("%d ",dis[i]);printf("\n");return;
}int main()
{while(~scanf("%d%d",&n,&m)){init();for(int i=0;i<m;i++){scanf("%d%d%d",&aa,&bb,&cc);map[aa][bb]=cc;}memset(book,0,sizeof book);for(int i=1;i<=n;i++)//记录各个点到源点的距离；dis[i]=map[1][i];book[1]=1;Dijkstra();}return 0;
}

3.Bellman-Ford----解决负权边

思路：

Dijkstra算法虽然好，但是它不能解决带有负权边的图，但是Bellman-ford算法可以解决这个问题。

Bellman-ford算法很简单，核心代码只有4行，并且可以完美的解决带有负权边的图，代码如下：

for(int k=1; k<n; k++)for(int i=1; i<=m; i++)if(dis[v[i]]>dis[u[i]]+w[i])dis[v[i]]=dis[u[i]]+w[i];

上面的代码中，外层循环一共循环了n-1遍（n是定点的个数），内层循环一共循环了m次（枚举了每一条边）；

dis[ ]数组中存储的是源点到其余各个点的最短的距离；

u，v，w三个数组中存储边的信息：u是边的起点，v是边的终点，w是边的距离；

if(dis[v[i]]>dis[u[i]]+w[i])dis[v[i]]=dis[u[i]]+w[i];

 上面说了，dis[ ]数组中存储的是源点到其余各点的距离。那么这两行代码的意思是：试试能不能通过边u[i]-->v[i]这条边，把源点到v[i]的距离变小。

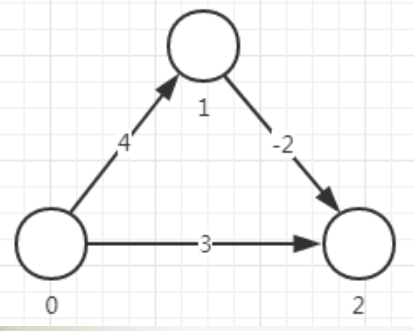
图例：

          

初始化后的结果：

   

第一轮松弛后的结果：

 

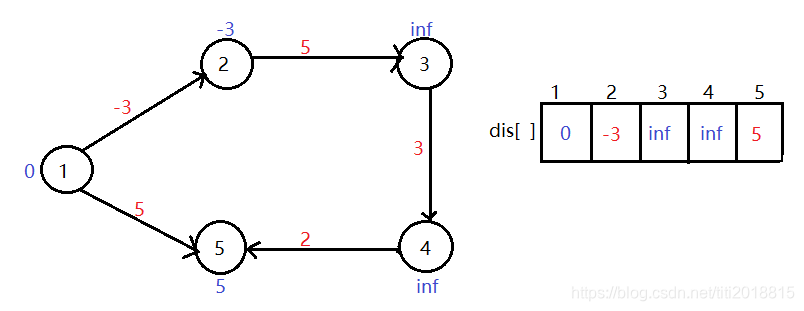
第二轮松弛后的结果：

 

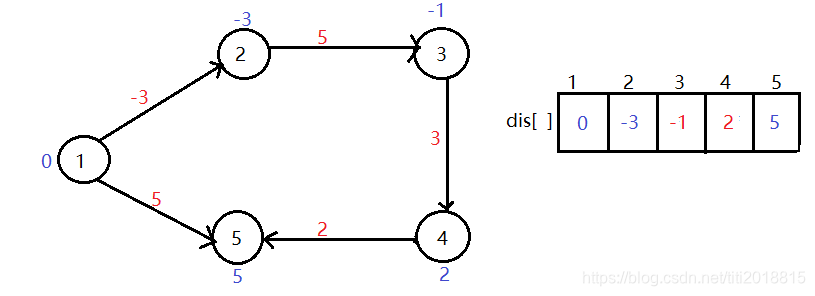
第三轮松弛后的结果：

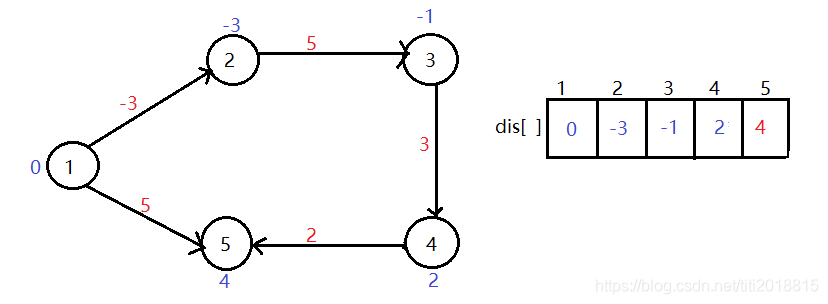
第四轮松弛后的结果：

代码如下：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;const int N=1010;
const int inf=99999999;int dis[N];
int k,n,m;
int u[N],v[N],w[N];void init()//初始化；
{for(int i=1; i<=n; i++)dis[i]=inf;
}void Bellman_Ford()
{dis[1]=0;for(int k=1; k<n; k++){for(int i=1; i<=m; i++){if(dis[v[i]]>dis[u[i]]+w[i])dis[v[i]]=dis[u[i]]+w[i];}}for(int i=1; i<=n; i++)printf("%d ",dis[i]);printf("\n");return ;
}int main()
{scanf("%d%d",&n,&m);init();for(int i=1; i<=m; i++){scanf("%d%d%d",&u[i],&v[i],&w[i]);}Bellman_Ford();return 0;
}

当然，Bellman-Ford算法也可以判断负权边，因为没有负权边的图中，进行n-1轮松弛后就该结束了，所以当有n-1轮松弛后就应该没有变化了，已经是最短的距离了；如果n-1轮松弛后还是能够改变最小的距离，那么就是有了负权边；

代码如下：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;const int N=1010;
const int inf=99999999;int dis[N];
int k,n,m;
int u[N],v[N],w[N];
int check,flag;void init()//初始化；
{for(int i=1; i<=n; i++)dis[i]=inf;
}void Bellman_Ford()
{dis[1]=0;for(int k=1; k<n; k++){check=0;for(int i=1; i<=m; i++){if(dis[v[i]]>dis[u[i]]+w[i]){dis[v[i]]=dis[u[i]]+w[i];check=1;}}if(check==0)//一轮下来没有变化，break;//说明dis数组已经是最短距离了，直接结束就可以了；}flag=0;//没有负权回路的图在n-1轮松弛后就应该结束了；for(int i=1; i<=m; i++)//如果在n-1轮后再进行一轮还是能松弛，{                      //那么就是有负权回路；if(dis[v[i]]>dis[u[i]]+w[i])flag=1;}if(flag==1)printf("此图有负权回路！\n");else{for(int i=1; i<=n; i++)printf("%d ",dis[i]);printf("\n");}return ;
}int main()
{scanf("%d%d",&n,&m);init();for(int i=1; i<=m; i++){scanf("%d%d%d",&u[i],&v[i],&w[i]);}Bellman_Ford();return 0;
}

4.SPFA算法（Bellman-Ford算法的队列优化）

思路：

每一次仅仅对最短路估计值发生变化的顶点的所有出边执行松弛操作；

把发生变化的顶点放入队列中进行维护；

每次选取队首的顶点u，对u的所有出边进行松弛操作，操作结束后就把顶点u出队列，再重复上面的操作；

需要注意的是，对于同一个顶点没必要同时多次存在于队列中，所以，我们需要一个队列来判重；

当然，我们要对于一个顶点的所有出点进行松弛操作，所以对于图的存储我们要改成用邻接表存储，不能再用邻接矩阵了；

代码如下：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;const int N=1010;
const int inf=99999999;int n,m;
int u[N],v[N],w[N];
int first[N],next[N];
int dis[N];//记录源点到各个点的最短距离；
int book[N];//记录哪个顶点进入到了队列中；
int que[N];//队列；
int head,tail,k;void init()
{for(int i=1; i<=n; i++)dis[i]=inf;memset(book,0,sizeof book);memset(first,-1,sizeof first);
}void solve()
{head=tail=1;que[tail]=1;tail++;book[1]=1;while(head<tail){k=first[que[head]];while(k!=-1){if(dis[v[k]]>dis[u[k]]+w[k]){dis[v[k]]=dis[u[k]]+w[k];if(book[v[k]]==0)//没有在队列中；{que[tail]=v[k];tail++;book[v[k]]=1;}}k=next[k];}book[que[head]]=0;head++;}return ;
}void print()
{for(int i=1; i<=n; i++)printf("%d ",dis[i]);printf("\n");
}int main()
{scanf("%d%d",&n,&m);init();//初始化；dis[1]=0;for(int i=1; i<=m; i++){scanf("%d%d%d",&u[i],&v[i],&w[i]);next[i]=first[u[i]];//建立邻接表；first[u[i]]=i;}solve();//解决问题；print();//输出结果；return 0;
}