哈夫曼树的构建及编码

声明：关于文件压缩，不是本文的重点，本文只说明并讨论哈夫曼树的构建和编码，不考虑文件压缩，实际上这个算法可以实现文件的压缩，但是我水平比较有限，涉及到文件操作，就不说了，另外本文后面编码和解码只是示范性举例型说明，并非真正实现了对文件的压缩。

如果对哈夫曼树文件压缩感兴趣，想要成型的代码，可以直接将自己电脑的文件实现实质性压缩，移步至哈夫曼树编码压缩

一、什么是哈夫曼树

百科：

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

解释：

“带权路径长度”：也就是WPL，它是所有“带权节点”的“权值(或者称为权重)”与距离根节点的“路径长度”乘积之和。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3Sm3ekhx-1622211552152)(D:\f2a8531350e394c2d2f7eaaddd1b04c6.jpeg)]

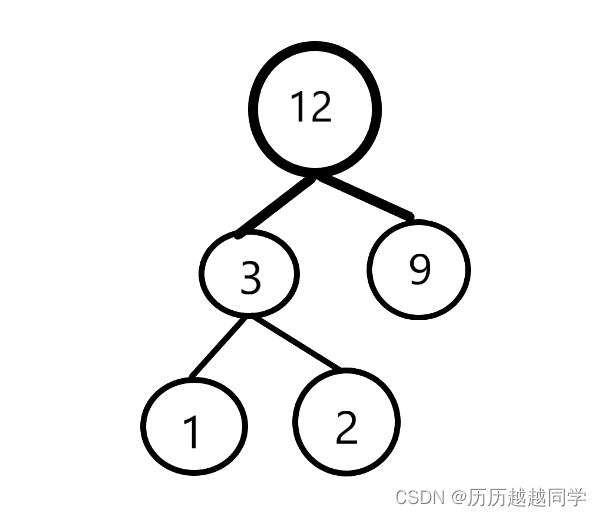
“带权节点”中存有原始数值，在建树过程中往往需要两个较小节点权值相加得到新节点再进行新一轮大小比较和筛选。比如如图5和3，它们的父母节点为8，但是，这个节点中的8并不是“原始”或者说不是“初始”数值，不能称为“带权节点”，所以图上该节点未作出标识，该节点确实存有8，但是不计入“带权路径长度”的计算中。

“路径长度”可看作该“带权节点”到根节点所要走的线段数，比如以图中3为例，显然有4段线段才能到根节点，所以3的“路径长度”为4。

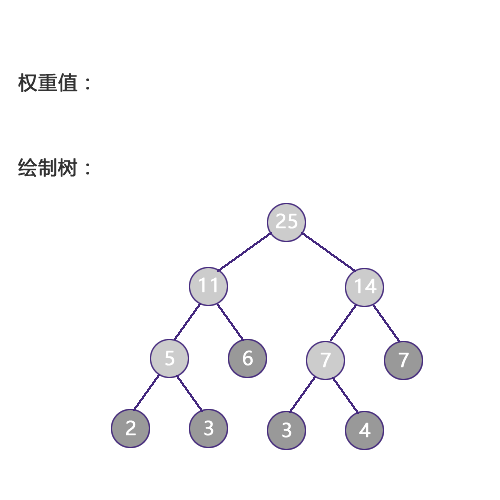
上图为例：带权路径长度计算

WPL = 3 * 4 + 5 * 4 + 11 * 3 + 23 * 2 + 29 * 2 + 14 * 3 + 7 * 4 + 8 * 4 = 271

注：哈夫曼树的创建虽然有规则，但是创建结果不是唯一的，我们唯一可以作为标准的不是树的形状或者结构，而是“带权路径”，即WPL，无论什么结构，WPL值一定唯一且相等！

二、什么是哈夫曼编码

哈夫曼编码即在哈夫曼树的基础上，左边路径标0，右边路径标1

举个例子，这时候，i可以表示为00，即从根往下读路径数字。

三、怎么建哈夫曼树、求哈夫曼编码

这里就不拿书里面做法说了，书上面是顺序存储，这里介绍链式存储。

方法 && 步骤：

1. 改造“轮子”，主要是利用C++中STL库中的“优先队列(priority_queue)"，优先队列(priority queue)介绍：

   普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

   优先队列的特性，假如是小根堆的有限队列，依次进队5 6 4 2 1那么，其实在队列中顺序是 1 2 4 5 6，队头为1，队尾元素为6，相当于通过进队，在队中实现了排序，接下来要取出较小元素，取出队头即可。

   上面就是对于“轮子”的介绍，接下来改造一下

   为啥要改造？因为加入是一个队列元素是一个数字，优先队列完全不用任何其他操作，自动按照数字大小排序，但是如果队列元素是一个结构体，结构体中包含很多数据，优先队列不知道按照哪一个数据进行排序，这时候就需要“重载”函数，对优先队列中默认的“元素的比较规则”实现自定义重构，然后把我们规定的规则加入 优先队列中即可

2. 经过改造轮子，我们可以轻松得两个较小节点。两个节点数值的和与两个较小节点构成“父母-左孩子-右孩子”，再将父母节点入优先队列。重复操作即可。便可实现构建哈夫曼树，下面是重载函数：

   struct myCmp
   {bool operator()(const tree &a, const tree &b){return a->data > b->data;}
   };
   

   构建哈夫曼树总代码：

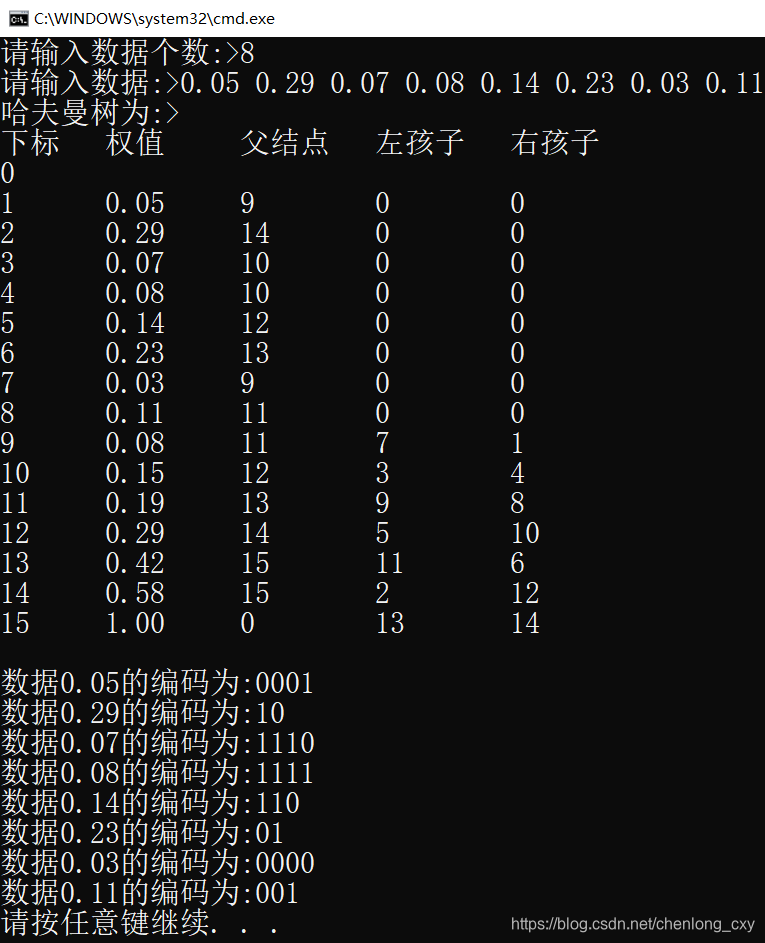
   #include <iostream>
   #include <vector>
   #include <cstdio>
   #include <string>
   #include <queue>
   #include <cstring>using namespace std;const int N = 1010;char st_c[N], str[N];
   //st_c[]数组存放输入的待编码的0-26英文字符
   //str[]数组读入原始带编码的英文字符，str_c[]数组存放的字
   //符是不同种类字符，无重复，而原始数组str[]中可能有重复
   int  st_n[N], ct_a;
   //st_n[]数组对应st_c[]中每个字符出现的次数
   double st_p[N];
   //st_p[]数组对应st_c[]中每个字符出现的比率
   char xtr[100], st_t[100][N];
   //xtr[]数组用来存放路径结果0/1
   typedef struct node
   {double data;struct node* lc, *rc;}node, * tree;struct myCmp
   {bool operator()(const tree &a, const tree &b){return a->data > b->data;}
   };void to_be_node(tree &T, tree T1, tree T2, double x)
   {T = new node;T->data = x;T->lc = T1, T->rc = T2;return;
   }int In(char ch)
   {for (int i = 1; st_c[i]; ++ i){if (st_c[i] == ch) return i;}return 0;
   }void preorder(tree &T, int cnt)//递归实现“编码”
   //类似于DFS(深度优先搜索)
   {	
   //    cout << "cnt = " << cnt << endl;if (!T->lc && !T->rc)//递归出口{int temp = 0;for (int i = 1; st_p[i]; ++ i){if (st_p[i] == T->data) { 
   //			   cout << "i = " << i << ' ' << "xtr = " << xtr << endl;st_p[i] = -1;//防止出现概率相同的，第二次把第一次盖了 strcpy(st_t[i], xtr);//找到带权节点，拷贝路径到st_t[]数组中return;} } return;}xtr[cnt] = '0';//左边走路径为0preorder(T->lc, cnt+1);xtr[cnt] = '1';//右边走路径为1preorder(T->rc, cnt+1);xtr[cnt] = '\0';//一条路搜完了,回退，清空后一步的0/1
   }void preordtraver(tree T)//先序遍历
   {if (T == NULL) return;cout << T->data << endl;preordtraver(T->lc);preordtraver(T->rc);
   }tree build_hfmtree()//构建哈夫曼树
   {priority_queue <tree, vector<tree>, myCmp> hm;//优先队列int judge, i = 1, j = 0;cin >> str;while (str[j]){ct_a ++;judge = In(str[j]);if (judge) st_n[judge] ++;else {st_c[i] = str[j];st_n[i] ++, i ++;}j ++; }cout << "占比如下：" << endl;for (int i = 1; st_c[i]; ++ i){st_p[i] = (double)st_n[i] / ct_a;cout << st_c[i] << ' ' << st_p[i] << endl;} cout << endl << endl;//将每个节点进队for (int i = 1; st_p[i]; ++ i) {node* T = new node;to_be_node(T, NULL, NULL, st_p[i]);hm.push(T);}while (hm.size() && hm.size() != 1)//当队中仅有1个节点时退出，这时候树就建成了。{node* t1 = hm.top(); hm.pop();node* t2 = hm.top(); hm.pop();node* T = NULL;to_be_node(T, t1, t2, t1->data + t2->data);hm.push(T);}node* T = hm.top(); hm.pop();//返回哈夫曼树根节点的指针return T;
   } void encode()
   {FILE *fp = NULL;fp = fopen("D:/HDU/teile.txt", "w");//建文件，路径自己写if (fp == NULL) {cout << "sbai!" << endl;exit(0); }for (int i = 0; str[i]; ++ i)//将哈夫曼码写入文件{int s = In(str[i]);fputs(st_t[s], fp);}fclose(fp);
   }void decode()
   {FILE *fp = NULL;char ch, cstr[N] = {0}, cx[N] = {0};fp = fopen("D:/HDU/teile.txt", "r");//打开文件if (fp == NULL) {cout << "sbai!!" << endl;exit(0); }int i = 0;while (!feof(fp))//读取文件中字符{ch = fgetc(fp);cstr[i ++] = ch;for (int j = 1; st_c[j]; ++ j){if (!strcmp(cstr, st_t[j]))//进行解码{cout << st_c[j];while (i) cstr[i --] = '\0';break;}}}fclose(fp);return;
   }int main()
   {	tree T = build_hfmtree();cout << "哈夫曼树建立完成！" << endl; cout << "*******前缀码*****" << endl << endl;preorder(T, 0);for (int i = 1; st_c[i]; ++ i) cout << st_c[i] << " : "<< st_t[i] << endl; cout << "******************" << endl << endl;encode();cout << "文件解密如下：\n";decode();return 0;
   }
   //测试：AAAAABBBBBBBBBBBBBBBBBBBBBBBBBBBBBCCCCCCCDDDDDDDDEEEEEEEEEEEEEEFFFFFFFFFFFFFFFFFFFFFFFGGGHHHHHHHHHHH
   /*-------------------------测试时间：2021.5.26  21：25------------------------*//*运行结果： 
   part 1.文件 
   1111111111111111111111111101010101010101010101010101010101010101010101
   0101010101010111011101110111011101110111000000000000000000000000011011
   0110110110110110110110110110110110110010101010101010101010101010101010
   1010101010101111101111011110001001001001001001001001001001001part 2. 运行窗口
   AAAAABBBBBBBBBBBBBBBBBBBBBBBBBBBBBCCCCCCCDDDDDDDDEEEEEEEEEEEEEEFFFFFFFFFFFFFFFFFFFFFFFGGGHHHHHHHHHHH
   占比如下：
   A 0.05
   B 0.29
   C 0.07
   D 0.08
   E 0.14
   F 0.23
   G 0.03
   H 0.11哈夫曼树建立完成！
   *******前缀码*****A : 11111
   B : 10
   C : 1110
   D : 000
   E : 110
   F : 01
   G : 11110
   H : 001
   ******************文件解密如下：
   AAAAABBBBBBBBBBBBBBBBBBBBBBBBBBBBBCCCCCCCDDDDDDDDEEEEEEEEEEEEEEFFFFFFFFFFFFFFFFFFFFFFFGGGHHHHHHHHHHH*/
   

四、为什么哈夫曼编码能实现压缩

这个很难解释，查资料吧…哈夫曼编码

---

THE END…